FWL定理#
FWL定理
目的変数のベクトル\(Y \in \mathbb{R}^{n\times 1}\)、説明変数の行列\(X \in \mathbb{R}^{n\times d}\)と誤差項\(e \in \mathbb{R}^{n\times 1}\)による線形回帰モデル
があるとする。
説明変数を\(X = (X_1 | X_2)\)と2つのグループに分割し、回帰係数ベクトル\(\beta\)も合わせて\(\beta = (\beta_1 | \beta_2)^T\)と2つに分割して
と表す。
この回帰モデルの\(\beta_1\)は、残差回帰(residual regression)と呼ばれる以下の手順に従うことでも得ることができる。
\(X_1\)を\(X_2\)に回帰して残差\(\tilde{X}_1\)を得る:\(\tilde{X}_1 = X_1 - X_2 \hat{\delta}\)
\(Y\)を\(X_2\)に回帰して残差\(\tilde{Y}\)を得る:\(\tilde{Y} = Y - X_2 \hat{\gamma}\)
\(\tilde{Y}\)を\(\tilde{X}_1\)に回帰させる:\(\tilde{Y} = \tilde{X}_1 \beta_1\)
証明#
残差への回帰\(\tilde{Y} = \tilde{X}_1 \beta_1\)は
であり、
を代入するとそれぞれ
となる。
これらをそれぞれ被説明変数、説明変数として最小二乗推定すると
(\(I - X_2 (X_2^T X_2)^{-1} X_2^T\)は冪等で対称な行列のため2行目で計算が簡略化できている)
次に、すべての説明変数\(X\)を\(Y\)に回帰したとき
の\(X_1\)の係数\(\beta_1\)の推定量を求める。二乗誤差の最小化の解
の1階の条件は
となる。\(\hat{\beta}_2\)を消すためには、2つ目の式に左から\(-X_1^T X_2(X_2^T X_2)^{-1}\)を掛けて
これを第1式に足すと
となる。
これを変形すると
となり、残差回帰の解と一致する。
数値例#
import numpy as np
n = 100
d = 4
k = 1
np.random.seed(0)
beta = np.array(list(range(1, d + 1)))
print(f"{beta=}")
X = np.random.uniform(size=(n, d))
e = np.random.normal(size=n) * 0.1
Y = X @ beta + e
X1 = X[:, :k]
X2 = X[:, k:]
beta1 = beta[:k]
beta2 = beta[k:]
assert np.allclose(Y, X1 @ beta1 + X2 @ beta2 + e)
beta=array([1, 2, 3, 4])
# I - X_2 (X_2^T X_2)^{-1} X_2^T は冪等で対称な行列
I = np.eye(n)
M = (I - X2 @ np.linalg.inv(X2.T @ X2) @ X2.T)
assert np.allclose(M.T, M)
assert np.allclose(M, M @ M)
delta = np.linalg.inv(X2.T @ X2) @ X2.T @ X1
gamma = np.linalg.inv(X2.T @ X2) @ X2.T @ Y
Y_tilde = (Y - X2 @ gamma)
X_tilde = (X1 - X2 @ delta)
# 残差回帰
beta_hat2 = np.linalg.inv(X_tilde.T @ X_tilde) @ X_tilde.T @ Y_tilde
beta_hat2.round(1)
array([1.])
# 通常の線形回帰
beta_hat1 = np.linalg.inv(X.T @ X) @ X.T @ Y
beta_hat1.round(1)
array([1. , 2. , 2.9, 4. ])
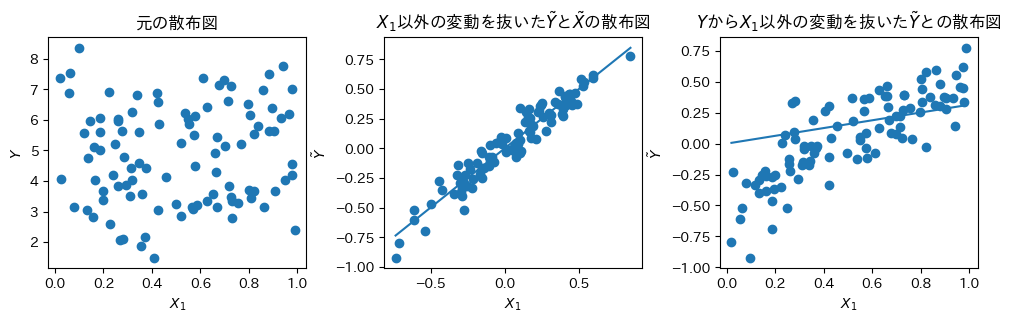
残差の作図#
Show code cell source
import matplotlib.pyplot as plt
import japanize_matplotlib
fig, axes = plt.subplots(figsize=[12, 3], ncols=3)
fig.subplots_adjust(wspace=0.3)
axes[0].scatter(X1, Y)
axes[0].set(ylabel=r"$Y$", xlabel=r"$X_1$", title="元の散布図")
axes[1].scatter(X_tilde, Y_tilde)
axes[1].set(ylabel=r"$\tilde{Y}$", xlabel=r"$X_1$", title=r"$X_1$以外の変動を抜いた$\tilde{Y}$と$\tilde{X}$の散布図")
beta_ = np.linalg.inv(X_tilde.T @ X_tilde) @ X_tilde.T @ Y_tilde
xrange = np.linspace(X_tilde.min(), X_tilde.max(), 100)
axes[1].plot(xrange, xrange.reshape(-1, 1) @ beta_)
axes[2].scatter(X1, Y_tilde)
axes[2].set(ylabel=r"$\tilde{Y}$", xlabel=r"$X_1$", title=r"$Y$から$X_1$以外の変動を抜いた$\tilde{Y}$との散布図")
beta_ = np.linalg.inv(X1.T @ X1) @ X1.T @ Y_tilde
xrange = np.linspace(X1.min(), X1.max(), 100)
axes[2].plot(xrange, xrange.reshape(-1, 1) @ beta_)
fig.show()
外生性・直交条件からの説明#
浅野・中村では誤差が直交することから証明するスタイルで、有斐閣の本はより直接的に証明している
OLSのPartialling out解釈#
というモデルの\(\beta_1\)は
\(y\)を\(x_1\)に回帰する:\(y = \beta_0 + \beta_1 x_1 + \beta_2 z_2 + \varepsilon\)
\(y\)を\(\tilde{x}_1\)に回帰する(ここで\(\tilde{x}_1\)は\(x_1\)を\(x_2\)に回帰した残差)
\(\tilde{y}\)を\(\tilde{x}_1\)に回帰する(ここで\(\tilde{y}\)は\(y\)を\(x_2\)に回帰した残差)
の3つの方法のいずれかで推定することができる
数値例#
import numpy as np
n = 1000
np.random.seed(0)
x0 = np.ones(shape=(n, ))
x2 = np.random.uniform(0, 1, size=n)
x1 = 3 * x2 + np.random.uniform(0, 1, size=n) + np.random.normal(0, 1, size=n)
X = np.array([ x0, x1, x2 ]).T
e = np.random.normal(0, 1, size=n)
beta = np.array([10, 5, 7]) # 真のbeta
y = X @ beta + e
np.corrcoef(X, rowvar=False)
/usr/local/lib/python3.10/site-packages/numpy/lib/function_base.py:2897: RuntimeWarning: invalid value encountered in divide
c /= stddev[:, None]
/usr/local/lib/python3.10/site-packages/numpy/lib/function_base.py:2898: RuntimeWarning: invalid value encountered in divide
c /= stddev[None, :]
array([[ nan, nan, nan],
[ nan, 1. , 0.64601675],
[ nan, 0.64601675, 1. ]])
class OLS:
def fit(self, X, y):
self.beta_ = np.linalg.inv(X.T @ X) @ X.T @ y
return self
def predict(self, X):
return X @ self.beta_
1. \(y\)を\(x_1\)に回帰する#
\(y = \beta_0 + \beta_1 x_1 + \beta_2 z_2 + \varepsilon\)
# 1. 𝑦 を 𝑥1 に回帰する
OLS().fit(X, y).beta_
array([9.98226817, 5.03640436, 6.80111723])
2. \(y\)を\(\tilde{x}_1\)に回帰する#
ここで\(\tilde{x}_1\)は\(x_1\)を\(x_2\)に回帰した残差
# 2. 𝑦 を 𝑥̃ 1 に回帰する
X_ = X[:, [0, 2]] # x0, x2だけのX
x1_res = x1 - OLS().fit(X_, x1).predict(X_)
# 切片を付けた場合
X_ = np.array([ x0, x1_res ]).T
OLS().fit(X_, y).beta_
array([23.29878836, 5.03640436])
# 切片を付けない場合
OLS().fit(x1_res.reshape(-1, 1), y).beta_
array([5.03640436])
3. \(\tilde{y}\)を\(\tilde{x}_1\)に回帰する#
ここで\(\tilde{y}\)は\(y\)を\(x_2\)に回帰した残差
# 3. 𝑦̃ を 𝑥̃ 1 に回帰する
X_ = X[:, [0, 2]] # x0, x2だけのX
y_res = y - OLS().fit(X_, y).predict(X_)
# 切片を付けない場合
OLS().fit(x1_res.reshape(-1, 1), y_res).beta_
array([5.03640436])
# 切片を付けた場合
X_ = np.array([ x0, x1_res ]).T
OLS().fit(X_, y_res).beta_
array([8.32667268e-17, 5.03640436e+00])
partialling out#
OLS推定では説明変数と残差の共分散はゼロになる。
というモデルがあったとき、説明変数\(x_j\)を他のすべての説明変数に回帰すると、その残差\(\tilde{x}_j\)は説明変数\(x_j\)の分散の情報を残す一方で他の説明変数とは無相関になる。
したがって\(y\)をこの残差\(\tilde{x}_j\)に回帰すると、その回帰係数\(\beta_j\)は\(y\)に対する\(x_j\)の影響のみを示す。
→他の変数の影響を排除(partialling out)できる
FWL定理の応用#
データの可視化#
元のモデルに\(d\)次元の説明変数があったとしても、\(\tilde{x}_j\)と\(y\)の関係へと次元を削減することができるため、グラフに表示しやすい。
計算の高速化#
PyHDFEパッケージのような高次元データの分析において活用されているらしい
統計的因果推論#
I am referring to the work on post-double selection by Belloni, Chernozhukov, Hansen (2013) and the follow up work on “double machine learning” by Chernozhukov, Chetverikov, Demirer, Duflo, Hansen, Newey, Robins (2018).
Belloni et al. (2014)のpost-double selection
Chernozhukov et al. (2018)のDouble/debiased machine learning
References#
FWL
Frisch, R., & Waugh, F. V. (1933). Partial time regressions as compared with individual trends. Econometrica: Journal of the Econometric Society, 387-401.
Lovell, M. C. (1963). Seasonal adjustment of economic time series and multiple regression analysis. Journal of the American Statistical Association, 58(304), 993-1010.
(考察)再帰的なpartialling outで任意のパラメータを任意の次元で推定できないか?#
→ できなかった
うまくいってAdditive modelとのつながりが見えれば面白かったんだが
import numpy as np
n = 1000
np.random.seed(0)
x0 = np.ones(shape=(n, ))
x2 = np.random.uniform(0, 1, size=n)
x3 = np.random.uniform(0, 1, size=n)
x1 = x2 + x3 + np.random.normal(0, 1, size=n)
X = np.array([ x0, x1, x2, x3 ]).T
e = np.random.normal(0, 1, size=n)
beta = np.array([10, 5, 7, 3]) # 真のbeta
y = X @ beta + e
class OLS:
def fit(self, X, y):
self.beta_ = np.linalg.inv(X.T @ X) @ X.T @ y
return self
def predict(self, X):
return X @ self.beta_
1. \(y\)を\(x_1\)に回帰する#
\(y = \beta_0 + \beta_1 x_1 + \beta_2 z_2 + \varepsilon\)
# 1. 𝑦 を 𝑥1 に回帰する
OLS().fit(X, y).beta_
array([9.95538609, 5.03200117, 6.87766976, 3.05740035])
2. \(y\)を\(\tilde{x}_1\)に回帰する#
ここで\(\tilde{x}_1\)は\(x_1\)を残りの説明変数に回帰した残差
# 2. 𝑦 を 𝑥̃ 1 に回帰する
X_ = X[:, [0, 2, 3]]
x1_res = x1 - OLS().fit(X_, x1).predict(X_)
# 切片を付けない場合
OLS().fit(x1_res.reshape(-1, 1), y).beta_
array([5.03200117])
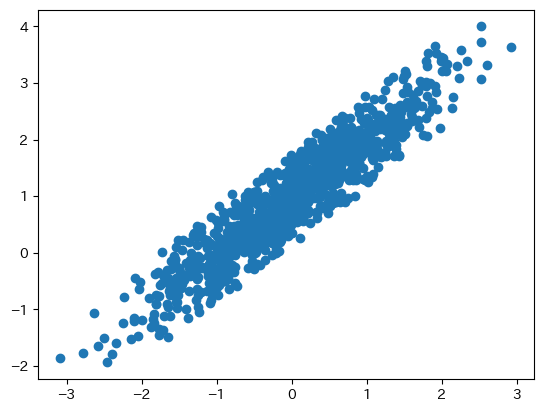
import matplotlib.pyplot as plt
plt.scatter(x1_res, x1)
<matplotlib.collections.PathCollection at 0x7fcac01fc400>
from scipy.stats import pearsonr
pearsonr(x1_res, x1).statistic.round(3)
0.933
説明変数1つずつでpartialling outできないか?
\(\tilde{x}_1 = x_1 - \hat{\beta}_0 x_0\)
\(\tilde{x}_1 = \tilde{x}_1 - \hat{\beta}_2 x_2\)
\(\tilde{x}_1 = \tilde{x}_1 - \hat{\beta}_3 x_3\)
for all nuisance parameter indices \(j \in J\)
\(\newcommand{\argmin}{\mathop{\arg\min}} \hat{\beta}_j = \argmin_{\beta_j} E[(y - \beta_j x_j)^2]\)
\(\tilde{x}_j = y - \hat{\beta}_j x_j\)
# 2. 𝑦 を 𝑥̃ 1 に回帰する
x1_res = x1.copy()
nuisance_indices = [0, 2, 3]
for i in nuisance_indices:
X_ = X[:, [i]]
x1_res = x1_res - OLS().fit(X_, x1_res).predict(X_)
print(f"corr(x1_res, x1): {pearsonr(x1_res, x1).statistic:.3f}")
print(f"beta1 : {OLS().fit(x1_res.reshape(-1, 1), y).beta_[0]:.3f}")
OLS().fit(x1_res.reshape(-1, 1), y).beta_
corr(x1_res, x1): 1.000
beta1 : 5.750
corr(x1_res, x1): 0.998
beta1 : 3.435
corr(x1_res, x1): 0.998
beta1 : 2.925
array([2.92542108])
# 2. 𝑦 を 𝑥̃ 1 に回帰する
x1_res = x1.copy()
nuisance_indices = [0, 2, 3]
for i in nuisance_indices[::-1]:
X_ = X[:, [i]]
x1_res = x1_res - OLS().fit(X_, x1_res).predict(X_)
print(f"corr(x1_res, x1): {pearsonr(x1_res, x1).statistic:.3f}")
print(f"beta1 : {OLS().fit(x1_res.reshape(-1, 1), y).beta_[0]:.3f}")
OLS().fit(x1_res.reshape(-1, 1), y).beta_
corr(x1_res, x1): 0.887
beta1 : 7.193
corr(x1_res, x1): 0.876
beta1 : 2.998
corr(x1_res, x1): 0.876
beta1 : 4.613
array([4.61310126])