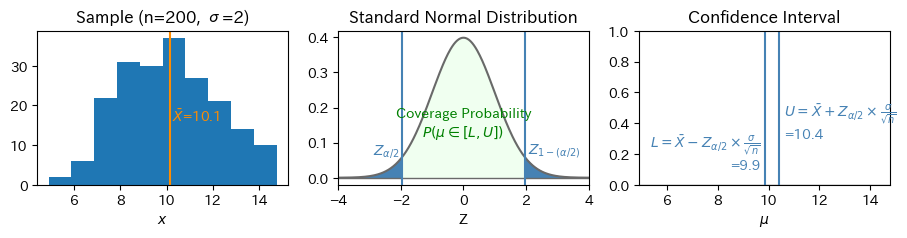
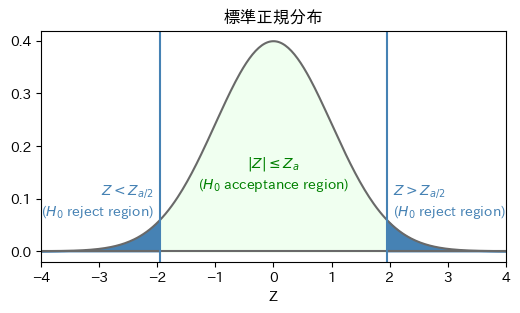
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy.stats import norm

n = 200
sigma = 2
x = norm.rvs(loc=10, scale=sigma, size=n, random_state=0)
x_bar = x.mean()

fig, axes = plt.subplots(dpi=100, figsize=[11, 2], ncols=3)
# Histogram
axes[0].set(title=f"Sample (n={n}, σ={sigma})", xlabel="$x$")
axes[0].hist(x, bins=10)
axes[0].axvline(x=x_bar, color="darkorange")
axes[0].text(x_bar + 0.1, n*0.08, r"$\bar{X}$"+f"={x_bar:.1f}", color="darkorange", horizontalalignment="left")


# Z and Standard Normal Dist
z = np.linspace(-4, 4, 300)
y = norm.pdf(z)
axes[1].set(title="Standard Normal Distribution", xlabel="Z", xlim=(-4, 4))
axes[1].plot(z, y, color="dimgray")
axes[1].axhline(y=0, color="dimgray", linewidth=1)
alpha = 0.05 / 2
for a in [alpha, (1 - alpha)]:
    z_ = norm.ppf(a)
    axes[1].axvline(x=z_, color="steelblue")
    if z_ < 0:
        axes[1].text(z_ - 0.1, norm.pdf(z_) + 0.01, r"$Z_{\alpha/2}$", color="steelblue", horizontalalignment="right")
        axes[1].fill_between(z, 0, y, where = z <= z_, color="steelblue")
    else:
        axes[1].text(z_ + 0.1, norm.pdf(z_) + 0.01, r"$Z_{1-(\alpha/2)}$", color="steelblue", horizontalalignment="left")
        axes[1].fill_between(z, 0, y, where = z >= z_, color="steelblue")

is_accept = np.abs(z) <= norm.ppf(a)
axes[1].fill_between(z[is_accept], 0, y[is_accept], color="honeydew")
axes[1].text(0, norm.pdf(0) * 0.3, "Coverage Probability\n$P(\mu \in [L, U])$", color="green", horizontalalignment="center")


# Confidence interval
xlim = (x.min(), x.max())
x_space = np.linspace(xlim, 300)
y = norm.pdf(x_space)
axes[2].set(title="Confidence Interval", xlabel=r"$\mu$", xlim=xlim)
axes[2].axhline(y=0, color="dimgray", linewidth=1)

alpha = 0.05 / 2
for a in [alpha, (1 - alpha)]:
    z_ = norm.ppf(a)
    lower_or_upper = x_bar + z_ * (sigma / np.sqrt(n))
    axes[2].axvline(x=lower_or_upper, color="steelblue")
    if z_ < 0:
        axes[2].text(lower_or_upper - 0.2, 0.1, r"$L=\bar{X} - Z_{\alpha/2} \times \frac{\sigma}{\sqrt{n}}$" + f"\n={lower_or_upper:.1f}", color="steelblue", horizontalalignment="right")
    else:
        axes[2].text(lower_or_upper + 0.2, 0.3, r"$U=\bar{X} + Z_{\alpha/2} \times \frac{\sigma}{\sqrt{n}}$" + f"\n={lower_or_upper:.1f}", color="steelblue", horizontalalignment="left")

fig.show()

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy.stats import norm

z = np.linspace(-4, 4, 300)
y = norm.pdf(z)

fig, ax = plt.subplots(dpi=100, figsize=[6, 3])
ax.set(title="標準正規分布", xlabel="Z", xlim=(-4, 4))
ax.plot(z, y, color="dimgray")
ax.axhline(y=0, color="dimgray", linewidth=1.5)

# 区間推定
alpha = 0.05 / 2
for a in [alpha, (1 - alpha)]:
    x = norm.ppf(a)
    ax.axvline(x=x, color="steelblue")
    if x < 0:
        ax.text(x - 0.1, norm.pdf(x) + 0.01, "$Z < Z_{a/2}$\n($H_0$ reject region)", color="steelblue", horizontalalignment="right")
        ax.fill_between(z, 0, y, where = z <= x, color="steelblue")
    else:
        ax.text(x + 0.1, norm.pdf(x) + 0.01, "$Z > Z_{a/2}$\n($H_0$ reject region)", color="steelblue", horizontalalignment="left")
        ax.fill_between(z, 0, y, where = z >= x, color="steelblue")


# 仮説検定
is_accept = np.abs(z) <= norm.ppf(a)
ax.fill_between(z[is_accept], 0, y[is_accept], color="honeydew")
ax.text(0, norm.pdf(0) * 0.3, "$|Z| \leq Z_a$\n($H_0$ acceptance region)", color="green", horizontalalignment="center")

fig.show()