練習問題メモ 02#
和達三樹. (2019). 微分積分. 第3章 練習問題
[4] 次の関数の\(n\)次導関数を求めよ#
(1) \(y=\frac{1}{x}\)
\(y=x^{-1}\)なので
\(n=1\)のとき、\(f'(x) = -1 \cdot x^{-2}\)
\(n=2\)のとき、\(f''(x) = -1 \cdot (-2) \cdot x^{-3}\)
\(n=3\)のとき、\(f^{(3)}(x) = -1 \cdot (-2) \cdot (-3) x^{-4}\)
\(n=4\)のとき、\(f^{(4)}(x) = -1 \cdot (-2) \cdot (-3) \cdot (-4) x^{-5}\)
よって一般に
\[
f^{(n)}(x) = (-1)^{n} n! x^{-(n+1)}
\]
(2) \(y=a^x \quad (a>0)\)
\((a^x)' = a^x \log a\)
\[\begin{split}
\log y = x \log a\\
\to x = \frac{\log y}{\log a}
\end{split}\]
\[\begin{split}
\frac{dx}{dy} = \frac{1}{y \log a}\\
\frac{dy}{dx} = 1 / \frac{dx}{dy}\\
= y \log a\\
= a^x \log a
\end{split}\]
\((a^x)'' = a^x (\log a)^2\)
\[\begin{split}
\log y' = x \log a + \log \log a\\
\to x = \frac{\log y' - \log\log a}{\log a}
\end{split}\]
\[
\frac{dx}{dy} = \left(
\frac{\log y'}{\log a}
- \frac{\log\log a}{\log a}
\right)'
= \frac{1}{\log a} \frac{1}{y}
\]
\[\begin{split}
\frac{dy}{dx} = 1 / \frac{dx}{dy}\\
= y \log a\\
= a^x \log a \log a
\end{split}\]
\[
f^{(n)}(x) = \frac{d^n}{dx} a^x
= a^x (\log a)^n
\]
(3) \(y=x^2 e^x\)
ライプニッツの公式
\[
(f g)^{(n)}=\sum_{k=0}^n{ }_n \mathrm{C}_k f^{(k)} g^{(n-k)}
\]
を使って
\[\begin{split}
\begin{align}
(x^2 e^x)^{(n)}
&= \sum_{k=0}^n { }_n C_k (x^2)^{(k)} (e^x)^{(n-k)}\\
&= { }_n C_0 (x^2)^{(0)} (e^x)^{(n-0)}\\
&\quad+ { }_n C_1 (x^2)^{(1)} (e^x)^{(n-1)}\\
&\quad+ { }_n C_2 (x^2)^{(2)} (e^x)^{(n-2)}\\
&\quad+ { }_n C_3 (x^3)^{(3)} (e^x)^{(n-3)}\\
&\quad+ \cdots
\\
&= \frac{n!}{0!(n-0)!} x^2 e^x\\
&\quad + \frac{n!}{1!(n-1)!} 2x e^x\\
&\quad + \frac{n!}{2!(n-2)!} 2 e^x\\
&\quad (\because x^2 \text{ の 3階以上の微分は定数の微分になりゼロのため、以降の項は消える})
\\
&= \frac{n}{n} x^2 e^x\\
&\quad + \frac{n}{1} 2x e^x\\
&\quad + \frac{n (n-1)}{2} 2 e^x
\\
&= x^2 e^x + 2nx e^x + n(n-1) e^x
\\
&= e^x \{ x^2 + 2nx + n(n-1) \}
\end{align}
\end{split}\]
[5]#
[5] 助変数表示の微分 \(x\) と \(y\) が 1 つの変数 \(t\) の関数として \(x=f(t), y=g(t)\) の形で 与えられているとする. このとき, \(y\) は \(x\) の関数, または \(x\) は \(y\) の関数と考えてよく, \(t\) を助変数(パラメータ)または媒介変数という. 逆関数の微分法を利用すれば,
\[
\frac{d y}{d x}=\frac{d y}{d t} \frac{d t}{d x}=\frac{\frac{d y}{d t}}{\frac{d x}{d t}}=\frac{g^{\prime}(t)}{f^{\prime}(t)}
\]
によって, 導関数を計算できる. これを用いて, 次の関数について, \(d y / d x\) を求めよ.
(1) \(x=a \cos t, \quad y=b \sin t\)
\[\begin{split}
\frac{dy}{dt} = b \cos t\\
\frac{dx}{dt} = - a \sin t\\
\end{split}\]
なので
\[
\frac{d y}{d x} = \frac{\frac{d y}{d t}}{\frac{d x}{d t}}
= - \frac{b \cos t}{a \sin t}
= - \frac{b}{a} \cot t
\]
(2) \(\displaystyle x=\frac{3 a t}{1+t^3}, \quad y=\frac{3 a t^2}{1+t^3}\)
\[\begin{split}
\frac{dy}{dt}
= \frac{(3 a t^2)' (1+t^3) - (3 a t^2) (1+t^3)'}{ (1+t^3)^2 }\\
= \frac{6 a t (1+t^3) - 3 a t^2 \cdot 3t^2}{ (1+t^3)^2 }\\
= \frac{ 6at + 6at^4 - 9at^4}{ (1+t^3)^2 }\\
= \frac{ 6at - 3at^4}{ (1+t^3)^2 }\\
\end{split}\]
\[\begin{split}
\frac{dx}{dt}
= \frac{(3at)' (1+t^3) - 3at (1+t^3)'}{(1+t^3)^2}\\
= \frac{3a (1+t^3) - 3at \cdot 3t^2}{ (1+t^3)^2 }\\
= \frac{3a + 3a t^3 - 9at^3}{ (1+t^3)^2 }\\
= \frac{3a - 6at^3}{ (1+t^3)^2 }\\
\end{split}\]
なので
\[\begin{split}
\frac{d y}{d x} = \frac{\frac{d y}{d t}}{\frac{d x}{d t}}
= \frac{
\frac{ 6at - 3at^4 }{ (1+t^3)^2}
}{
\frac{ 3a - 6at^3 }{ (1+t^3)^2 }
}\\
= \frac{ 6at - 3at^4 }{ (1+t^3)^2}
\frac{ (1+t^3)^2 }{ 3a - 6at^3 }\\
= \frac{ 6at - 3at^4 }{ 3a - 6at^3 }\\
= \frac{ 1/3 }{ 1/3 } \frac{ 6at - 3at^4 }{ 3a - 6at^3 }\\
= \frac{ 2at - at^4 }{ a - 2at^3 }\\
= \frac{ a (2t - t^4) }{ a (1 - 2t^3) }\\
= \frac{ 2t - t^4 }{ 1 - 2t^3 }\\
= \frac{ t(2 - t^3) }{ 1 - 2t^3 }\\
\end{split}\]
[6]#
[6] 双曲線関数
\[
\sinh x=\frac{e^x-e^{-x}}{2}, \quad \cosh x=\frac{e^x+e^{-x}}{2}, \quad \tanh x=\frac{\sinh x}{\cosh x}
\]
に対して，次のことを示せ.
(1) \(\frac{d}{d x} \sinh x=\cosh x\)
(2) \(\frac{d}{d x} \cosh x=\sinh x\)
(3) \(\frac{d}{d x} \tanh x=\frac{1}{\cosh ^2 x}\)
(1) \(\frac{d}{d x} \sinh x=\cosh x\)
合成関数と捉えれば\((e^{-1\cdot x})' = - e^{-x}\) なので
\[
\frac{d}{d x} \sinh x
= \frac{d}{d x} \frac{e^x-e^{-x}}{2}
= \frac{e^x+e^{-x}}{2}
= \cosh x
\]
memo
\[\begin{split}
\frac{d}{d x} \sinh x
= \frac{d}{d x} \left( \frac{1}{2} e^x - \frac{1}{2} e^{-x} \right)\\
\end{split}\]
(2) \(\frac{d}{d x} \cosh x=\sinh x\)
合成関数と捉えれば\((e^{-1\cdot x})' = - e^{-x}\) なので
\[
\frac{d}{d x} \cosh x
= \frac{d}{d x} \frac{e^x+e^{-x}}{2}
= \frac{e^x-e^{-x}}{2}
= \sinh x
\]
(3) \(\displaystyle \frac{d}{d x} \tanh x=\frac{1}{\cosh ^2 x}\)
\[\begin{split}
\left(\frac{\sinh x}{\cosh x}\right)'
= \frac{(\sinh x)' \cosh x - \sinh x (\cosh x)'}{\cosh^2 x}\\
= \frac{\cosh^2 x - \sinh^2 x}{\cosh^2 x}\\
= \frac{1}{\cosh^2 x}\\
\end{split}\]
\(\cosh^2 x - \sinh^2 x = 1\)
\[\begin{split}
\begin{align}
\cosh^2 x - \sinh^2 x
&= (\cosh x + \sinh x)(\cosh x - \sinh x)\\
&= (\frac{e^x+e^{-x}}{2} + \frac{e^x-e^{-x}}{2})
(\frac{e^x+e^{-x}}{2} - \frac{e^x-e^{-x}}{2})\\
&= \frac{e^x+e^{-x} + e^x-e^{-x}}{2}
\frac{e^x+e^{-x} - e^x+e^{-x}}{2}\\
&= \frac{2 e^x}{2}
\frac{2 e^{-x}}{2}\\
&= e^x e^{-x}\\
&= e^{x-x}\\
&= 1
\end{align}
\end{split}\]
[7]#
[7] 次の関数の極値を求め, そのグラフの概形をかけ.
(1) \(f(x)=x^4+2 x^3-3 x^2-4 x+4\)
(2) \(f(x)=x e^x\)
(3) \(\displaystyle f(x)=\frac{x+4}{\sqrt{x^2+2 x+3}}\)
(1) \(f(x)=x^4+2 x^3-3 x^2-4 x+4\)#
極値
\[
f'(x) = 4 x^3 + 6 x^2 - 6 x - 4 = 0
\]
となる\(x\)を求める。
まず、因数\((x-a)\)の\(a\)を探索する。
因数定理より、\(f(a) = 0\)となる\(a\)があれば\((x - a)\)が因数になる。
\(a=1\)とすると\(f'(1) = 4 + 6 - 6 - 4 = 0\)なので\((x-1)\)が因数のひとつであることがわかった。
次に、組立除法で\((4x^3 + 6x^2 - 6x - 4) / (x-1)\)を求める
\[\begin{split}
\begin{array}{ccc}
4 & 6 & -6 & -4\\
& 4 & 10 & 4\\
\hline
4 & 10& 4 & 0
\end{array}
\end{split}\]
より商の\(4x^2 + 10x + 4\)と余り\(0\)が得られるので
\[
f'(x) = (x - 1)(4x^2 + 10x + 4)
\]
\(4x^2 + 10x + 4\)は、たすきがけ法などで解くと\((4x + 2)(x+2)\)なので
\[
f'(x) = (x - 1)(4x + 2)(x + 2)
\]
より、\(f'(x)=0\)となる\(x\)は\(-2, -1/2, 1\)
極値のひとつは
\[\begin{split}
f(-2) = (-2)^4 + 2 (-2)^3 - 3 (-2)^2 - 4 (-2) + 4\\
= 16 - 16 - 12 + 8 + 4\\
= 0
\end{split}\]
グラフ
\[\begin{split}
\begin{align}
f(-3)
&= (-3)^4 + 2 (-3)^3 - 3 (-3)^2 - 4 (-3) + 4\\
&= 81 - 54 - 27 + 12 + 4\\
&= 16\\
\\
f(-2)
&= (-2)^4 + 2 (-2)^3 - 3 (-2)^2 - 4 (-2) + 4\\
&= 16 - 16 - 12 + 8 + 4\\
&= 0\\
\\
f(-1)
&= 1 - 2 - 3 + 4 + 4\\
&= 4\\
\\
f(-1/2)
&= (-1/2)^4 + 2 (-1/2)^3 - 3 (-1/2)^2 - 4 (-1/2) + 4\\
&= \frac{1}{16} - 2 \frac{1}{8} - 3 \frac{1}{4} + 4 \frac{1}{2} + 4\\
&= \frac{1}{16} - \frac{1}{4} - \frac{3}{4} + 2 + 4\\
&= \frac{1}{16} + 5\\
\\
f(0) &= 4\\
f(1) &= 1 + 2 - 3 - 4 + 4\\
&= 0\\
\end{align}
\end{split}\]
Show code cell source
def f(x):
return x**4 + 2*x**3 - 3*x**2 - 4*x + 4
import numpy as np
import matplotlib.pyplot as plt
X = [-2, -1, -1/2, 0, 1]
fig, ax = plt.subplots(figsize=[4,2])
for x in X:
ax.scatter(x, f(x), color="steelblue")
ax.text(x, f(x), f"{(x, f(x))}")
x = np.linspace(min(X)-0.5, max(X)+0.5, 100)
ax.plot(x, f(x), color="steelblue")
ax.axvline(0, color="gray", alpha=0.7)
ax.axhline(0, color="gray", alpha=0.7)
ax.grid(True)
fig.show()
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-4, 3, 100)
fig, ax = plt.subplots(figsize=[4,2])
ax.plot(x, f(x), color="steelblue")
ax.axvline(0, color="gray", alpha=0.3)
ax.axhline(0, color="gray", alpha=0.3)
fig.show()
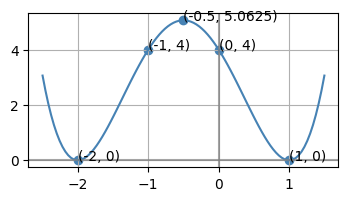
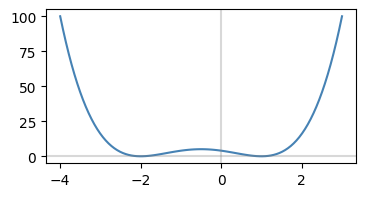
(2) \(f(x)=x e^x\)#
極値
\[\begin{split}
f'(x) = 1 \cdot e^x + x e^x = x e^x + e^x = 0\\
\to x = \frac{-e^x}{e^x}
= -1
\end{split}\]
\(f'(x)=0\)となる\(x\)は\(-1\)
極値は
\[
f(-1) = -1 e^{-1} = -\frac{1}{e} \approx -\frac{1}{2.718} \approx -0.368
\]
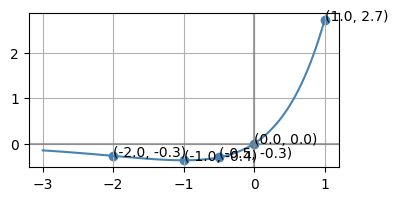
グラフ
\[\begin{split}
\begin{align}
f(-2) &= -2e^{-2} = -\frac{2}{e^2} \approx -0.27\\
f(-1) &= -e^{-1} = - \frac{1}{e} \approx -0.37\\
f(0) &= 0\\
f(1) &= e^{1} = e \approx 2.72\\
\end{align}
\end{split}\]
- 2 / np.exp(2)
-0.2706705664732254
- 1 / np.exp(1)
-0.36787944117144233
Show code cell source
def f(x):
return x * np.exp(x)
X = [-2, -1, -1/2, 0, 1]
fig, ax = plt.subplots(figsize=[4,2])
for x in X:
ax.scatter(x, f(x), color="steelblue")
ax.text(x, f(x), f"({x:.1f}, {f(x):.1f})")
x = np.linspace(-3, 1, 100)
ax.plot(x, f(x), color="steelblue")
ax.axvline(0, color="gray", alpha=0.7)
ax.axhline(0, color="gray", alpha=0.7)
ax.grid(True)
fig.show()
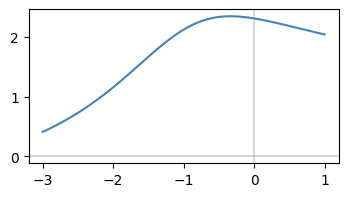
(3) \(f(x)=\frac{x+4}{\sqrt{x^2+2 x+3}}\)#
\[
f(x)= (x+4) (x^2 + 2x + 3)^{-1/2}
\]
なので、
\[\begin{split}
\begin{align}
f'(x)
&= (x+4)' (x^2 + 2x + 3)^{-1/2} + (x+4) ((x^2 + 2x + 3)^{-1/2})'\\
&= (x^2 + 2x + 3)^{-1/2} - \frac{1}{2} (x+4) (x^2 + 2x + 3)^{-3/2}\\
\end{align}
\end{split}\]
となり、
\[\begin{split}
(x^2 + 2x + 3)^{-3/2} = [(x + 1) + 2]^{-3/2} > 0\\
(\because [(x + 1) + 2] は x がなんであれ +2 部分により >0 のため)
\end{split}\]
のため、
わからなかった
略解だと\(x=-1/3\)
from sympy import symbols, factor
x = symbols("x")
y = (x**2 + 2*x + 3)**(-1/2) - (1/2) * (x+4) * (x**2 + 2*x + 3)**(-3/2)
factor(y)
\[\displaystyle - 2.0 \left(\frac{0.25 x}{\left(x^{2} + 2 x + 3\right)^{1.5}} + \frac{1.0}{\left(x^{2} + 2 x + 3\right)^{1.5}} - \frac{0.5}{\left(x^{2} + 2 x + 3\right)^{0.5}}\right)\]
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return (x+4)*(x**2 +2*x + 3)**(-1/2)
x = np.linspace(-3, 1, 100)
fig, ax = plt.subplots(figsize=[4,2])
ax.plot(x, f(x), color="steelblue")
ax.axvline(0, color="gray", alpha=0.3)
ax.axhline(0, color="gray", alpha=0.3)
fig.show()
