Quantized Training of LightGBM#
概要#
LightGBMのような最近のGBDTで使われている決定木では、葉の出力\(w\)は誤差関数の2次のテイラー近似をもとに、以下のように計算される（このあたりはChen & Guestrin, 2016が比較的わかりやすい）
ここで\(g_i\)は誤差関数の勾配、\(h_i\)は誤差関数の二次の微分である。
この\(g_i, h_i\)を32bitや64bitのfloatではなく、4bitなどの低ビット幅の整数で保持しよう、というのが量子化である。
現代的なGBDTの学習の流れ#
（Shi et al. (2022). Quantized training of gradient boosting decision trees.より）
まず、GBDTの学習の流れを再確認し、notationを決める
勾配ブースティング決定木（GBDT）は複数の決定木を組み合わせるアンサンブル学習のアプローチをとる。
各iterationでは現状の予測値に基づくGradientとHessianを計算し、負の勾配を近似するように決定木を学習する。
\(k+1\)回目の反復において、現状のサンプル\(i\)の予測値を\(\hat{y}_i^k\)とすると、誤差関数\(l\)のgradient\(g_i\)とhessian\(h_i\)は
となる。
葉\(s\)について、葉に含まれるデータの番号（index）の集合を\(I_s\)とする。葉\(s\)における\(g_i\)と\(h_i\)のサンプルについての合計を
と表記することにすると、反復\(k+1\)回目において木構造が固定された下で、訓練誤差は二次のテイラー近似により
と表すことができる。
ここで\(\mathcal{C}\)は定数で、\(w_s\)は葉\(s\)の予測値である。近似誤差の最小化により最適値が得られる
最適な木構造を探すのは困難であるため、木は貪欲かつ反復的に訓練される。
葉\(s\)を2つの子\(s_1, s_2\)に分割するとき、近似損失の減少分は次のように計算できる。
葉\(s\)にとっての最適な分割条件の探索は、すべての特徴のすべての分割候補点を数え上げて、最も損失の減少が多いものが選ばれる。
LightGBMでは最適分割点の探索を高速化するためにヒストグラムを使う。histogram based GBDTの基本的なアイデアは特徴量の値をbinsに分割する。histogramのbinsは、そのbinに含まれるデータのgradientsとhessiansの総和が記録されている。binsの境界値のみが分割候補点になる。
Algorithm 1 Histogram Construction for Leaf \(s\)
Input: Gradients \(\left\{g_1, \ldots, g_N\right\}\), Hessians \(\left\{h_1, \ldots, h_N\right\}\)
Input: Bin data data \([N][J]\), Data indices in leaf \(s\) denoted by \(I_s\)
Output: Histogram \({hist}_s\)
for \(i \in I_s, j \in\{1 \ldots J\}\) do
bin \(\leftarrow \operatorname{data}[i][j]\)
\(hist_s[j][bin] . g \leftarrow\) \(hist_s[j][\) bin \(] . g+g_i\)
\(hist_s[j][b i n] . h \leftarrow\) \(hist_s[j][b i n] . h+h_i\)
end for
伝統的には\(g_i\)と\(h_i\)には32-bitの浮動小数点数が使われ、histogramへの累計には32-bitか64-bitの浮動小数点数が必要になる。
Framework for Quantized Training#
まず\(g_i\)と\(h_i\)を低ビット幅（low-bitwidth）の整数\(\tilde{g}_i, \tilde{h}_i\)に量子化する。
すべての訓練サンプルの\(g_i\)と\(h_i\)のレンジを、等しい長さの区間へと分割する。\(B\)-bit \((B \geq 2)\) 整数の勾配を使うために、\(2^B - 2\)個の区間を使う。各区間の最後は整数値と対応するため、全体で\(2^B - 1\)個の整数値になる。
1次の導関数\(g_i\)は正の値も負の値もとるため、半分の区間は負の値のために割り当てられ、残り半分は正の値に割り当てられる。
2次の導関数\(h_i\)は一般的にGBDTで使われる誤差関数のほとんどすべてが非負の値をもつため、以下の議論では\(h_i \geq 0\)と仮定する。
それゆえ、区間の長さは\(g_i, h_i\)それぞれに対して
となる。これにより、低ビット幅の勾配は
で計算できる。ここで\(\text{Round}()\)は浮動小数点数を定数に丸める関数である。
なお、もし\(h_i\)が定数なら、量子化する必要はない。
詳細なrounding strategyは4.2節に書く。
Algorithm 1の\(g_i, h_i\)を\(\tilde{g}_i, \tilde{h}_i\)に置き換える。もとの勾配の和の計算は整数の和の計算に置き換えられ、histogram binsの統計量\(g\)と\(h\)は整数になる。
B = 2
g = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
delta_g = max([abs(gi) for gi in g]) / (2**(B-1) - 1)
tilde_g = [round(gi / delta_g) for gi in g]
tilde_g
[0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
分岐による損失の減少分
の\(G_{s_1}, H_{s_1}, G_{s_2}, H_{s_2}\)は整数の\(\tilde{G}_{s_1}, \tilde{H}_{s_1}, \tilde{G}_{s_2}, \tilde{H}_{s_2}\)に置き換えられる。
我々は2から4bitの量子化された勾配が十分よい精度をもたらすことを発見した。また、6.1節と7.4.3節で議論するが、ヒストグラムにおける累積した低ビット幅の勾配には16bit整数で十分であった。それゆえ、大部分の演算は低ビット幅の整数によって行われる。浮動小数点数の演算が必要になるのは本来の勾配とヘシアンとsplit gainを計算するときだけである。とくに、split gainは
と推定される。ここで勾配の統計量のスケールは\(\delta_g\)と\(\delta_h\)を乗じることで復元される。
Figure 1は量子化されたGBDTのワークフローを要約している。
Rounding Strategies and Leaf-Value Refitting#
最も近い整数への丸め込み（round-to-nearest）
では精度が大幅に低下することがわかった。
代わりに、 確率的な丸め込み（stochastic rounding）
を用いる（\(\text{w.p.}\)はwith probabilityの意味）。 確率的な丸め込みでは\(\mathbb{E}[\widetilde{g}_i]=g_i / \delta_g\)であるような値\(\widetilde{g}_i\)がランダムな値\(\lfloor g_i / \delta_g\rfloor\)か\(\lceil g_i / \delta_g\rceil\)をとる。
split gainは勾配の総和で計算されるため、確率的な丸め込みは総和への不偏推定量となる。すなわち
である。
確率的な丸め込みの重要性はニューラルネットの量子化学習[13]とDimBoost[16]のヒストグラム分解でも認識されている。
量子化された勾配により、最適なleaf valueは
となり、多くのケースで\(\widetilde{w}_s^*\)は良い結果をもたらすのに十分である。
しかし、ランキングなど一部の損失関数では、木の成長が止まったあとに元の勾配でleaf valueをrefittingする方法が精度を向上させることがわかった。BitBoost [8] も同様の方法をとっているが、BitBoostと違い、本手法はsplit gainのヘシアンを木の成長中も考慮するがBitBoostではヘシアンを定数として扱い真のヘシアンをleaf valueのrefittingのときだけ使う。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
def stochastic_round(x: float) -> int:
f = np.floor(x)
c = np.ceil(x)
return np.random.choice([f, c], p=[c - x, x - f])
np.random.seed(0)
e = 0.001
x = np.linspace(e, 1-e, 1000)
y = [stochastic_round(xi) for xi in x]
x_c = pd.cut(x, bins=10)
def mid_value(cat):
return cat.left + ((cat.right - cat.left) / 2)
cat_to_mid = {cat: mid_value(cat) for cat in x_c.categories}
df = pd.DataFrame({
"x": x,
"y": y,
"x_c": x_c.map(cat_to_mid, na_action=None)
})
agg = df.groupby("x_c", observed=True)["y"].agg(["mean", "std"]).reset_index()
fig, ax = plt.subplots()
ax.scatter(x, y, alpha=0.1, label="StochasticRound(x)", edgecolors="steelblue")
ax.errorbar(agg["x_c"], agg["mean"], yerr=agg["std"], alpha=0.9,
fmt="o", color="gray", label="mean & std of StochasticRound(x)")
# xerr=(x.max() - x.min()) / 10 / 2,
# for cat in x_c.categories:
# ax.axvline(cat.left, alpha=0.5, linestyle="--", color="gray")
# ax.axvline(cat.right, alpha=0.5, linestyle="--", color="gray")
ax.set(
xlabel="x",
ylabel="StochasticRound(x)",
title="",
)
ax.legend()
fig.show()
確率的な丸め込みによる#
確率的な丸め込みにより、「split gain推定の誤差は高い確率で小さい値に制限される」というsection 5の定理が提供できる。
実装#
注意点
精度を上げるため、量子化前の勾配でleaf valueを再計算する場合、計算時間もモデルのサイズも悪化する
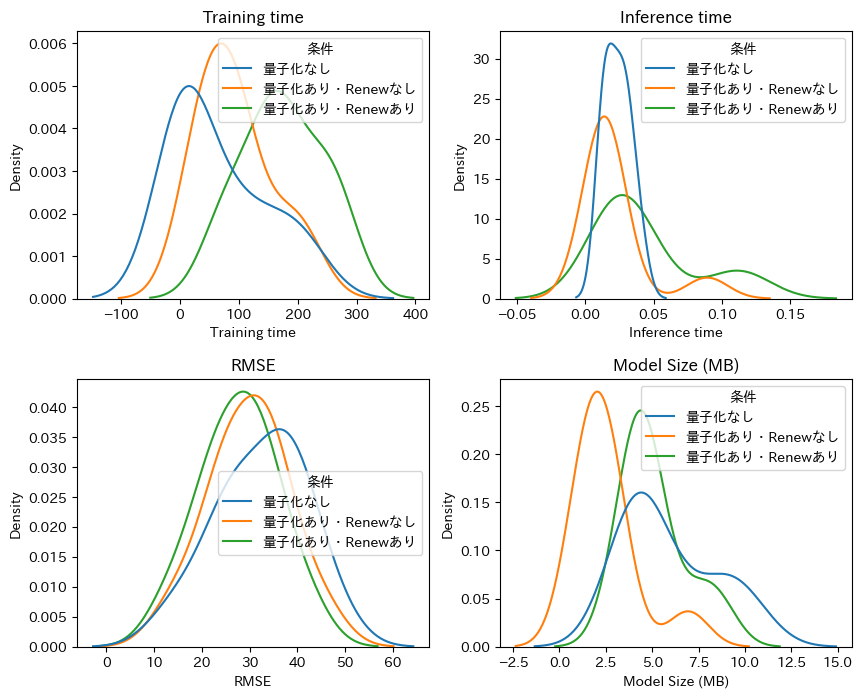
実験：量子化の有無による差を比較#
import lightgbm as lgb
print(f"{lgb.__version__=}")
def gen_dataset(seed=0):
from sklearn.datasets import make_regression
X, y = make_regression(n_samples=5_000, n_features=10, noise=0.5, random_state=seed)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8, random_state=0)
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, train_size=0.8, random_state=0)
import lightgbm as lgb
lgb_train = lgb.Dataset(X_train, y_train)
lgb_val = lgb.Dataset(X_val, y_val, reference=lgb_train)
return lgb_train, lgb_val, X_test, y_test
def train(params, lgb_train, lgb_val):
logs = {}
model = lgb.train(
params,
lgb_train,
num_boost_round=100_000,
valid_sets=[lgb_train, lgb_val],
callbacks=[
lgb.early_stopping(stopping_rounds=100),
lgb.log_evaluation(period=100000),
lgb.record_evaluation(logs)
]
)
return model, logs
from tqdm import tqdm
from time import time
from pathlib import Path
from sklearn.metrics import root_mean_squared_error
import joblib
import pandas as pd
def get_model_size(model):
model_path = Path("model.joblib")
with open(model_path, "wb") as f:
joblib.dump(model, f)
size_mb = model_path.stat().st_size / 1024**2
model_path.unlink()
return size_mb
def trials(name, params, n_trials=10):
train_times = []
pred_times = []
rmses = []
model_sizes = []
for i in tqdm(range(n_trials)):
lgb_train, lgb_val, X_test, y_test = gen_dataset(seed=i)
t0 = time()
model, _logs = train(params, lgb_train, lgb_val)
t1 = time()
train_times.append(t1 - t0)
t0 = time()
y_pred = model.predict(X_test)
t1 = time()
pred_times.append(t1 - t0)
rmse = root_mean_squared_error(y_test, y_pred)
rmses.append(rmse)
size = get_model_size(model)
model_sizes.append(size)
result = pd.DataFrame({
"Training time": train_times,
"Inference time": pred_times,
"RMSE": rmses,
"Model Size (MB)": model_sizes
})
result["条件"] = name
return result
import os
print(f"{os.cpu_count()=}")
n_trials = 10
results = []
params = {
'device_type': 'cpu',
'num_threads': os.cpu_count(),
'objective': 'mse',
'metric': 'rmse',
'num_leaves': 31,
'learning_rate': 0.1,
'feature_fraction': 0.8,
'verbose': -1,
'seed': 0,
'deterministic': True,
}
# 量子化なし
result = trials(name="量子化なし", params=params, n_trials=n_trials)
results.append(result)
# 量子化あり
params["use_quantized_grad"] = True
params["num_grad_quant_bins"] = 4
params["quant_train_renew_leaf"] = False
result = trials(name="量子化あり・Renewなし", params=params, n_trials=n_trials)
results.append(result)
params["quant_train_renew_leaf"] = True
result = trials(name="量子化あり・Renewあり", params=params, n_trials=n_trials)
results.append(result)
Show code cell output
lgb.__version__='4.5.0'
os.cpu_count()=4
0%| | 0/10 [00:00<?, ?it/s]
Training until validation scores don't improve for 100 rounds
Early stopping, best iteration is:
[1781] training's rmse: 0.115047 valid_1's rmse: 41.0182
10%|█ | 1/10 [00:01<00:12, 1.41s/it]
Training until validation scores don't improve for 100 rounds
20%|██ | 2/10 [00:02<00:10, 1.35s/it]
Early stopping, best iteration is:
[1650] training's rmse: 0.0972269 valid_1's rmse: 27.826
Training until validation scores don't improve for 100 rounds
Early stopping, best iteration is:
[3078] training's rmse: 0.00376388 valid_1's rmse: 46.6675
30%|███ | 3/10 [00:04<00:12, 1.77s/it]
Training until validation scores don't improve for 100 rounds
40%|████ | 4/10 [00:06<00:09, 1.58s/it]
Early stopping, best iteration is:
[1642] training's rmse: 0.119979 valid_1's rmse: 32.1281
Training until validation scores don't improve for 100 rounds
Early stopping, best iteration is:
[3313] training's rmse: 0.00137981 valid_1's rmse: 25.5328
50%|█████ | 5/10 [00:08<00:09, 1.88s/it]
Training until validation scores don't improve for 100 rounds
60%|██████ | 6/10 [00:09<00:06, 1.67s/it]
Early stopping, best iteration is:
[1616] training's rmse: 0.130356 valid_1's rmse: 36.1539
Training until validation scores don't improve for 100 rounds
Early stopping, best iteration is:
[3704] training's rmse: 0.000824281 valid_1's rmse: 39.8657
70%|███████ | 7/10 [00:12<00:06, 2.01s/it]
Training until validation scores don't improve for 100 rounds
80%|████████ | 8/10 [00:13<00:03, 1.70s/it]
Early stopping, best iteration is:
[1251] training's rmse: 0.252942 valid_1's rmse: 17.2222
Training until validation scores don't improve for 100 rounds
90%|█████████ | 9/10 [00:14<00:01, 1.53s/it]
Early stopping, best iteration is:
[1454] training's rmse: 0.237015 valid_1's rmse: 38.8602
Training until validation scores don't improve for 100 rounds
Early stopping, best iteration is:
[2294] training's rmse: 0.020392 valid_1's rmse: 23.7294
100%|██████████| 10/10 [00:16<00:00, 1.59s/it]
100%|██████████| 10/10 [00:16<00:00, 1.66s/it]
0%| | 0/10 [00:00<?, ?it/s]
Training until validation scores don't improve for 100 rounds
10%|█ | 1/10 [00:01<00:09, 1.07s/it]
Early stopping, best iteration is:
[1093] training's rmse: 0.508697 valid_1's rmse: 36.2037
Training until validation scores don't improve for 100 rounds
20%|██ | 2/10 [00:01<00:05, 1.34it/s]
Early stopping, best iteration is:
[427] training's rmse: 3.18506 valid_1's rmse: 24.8431
Training until validation scores don't improve for 100 rounds
30%|███ | 3/10 [00:02<00:05, 1.27it/s]
Early stopping, best iteration is:
[944] training's rmse: 0.878267 valid_1's rmse: 41.9654
Training until validation scores don't improve for 100 rounds
40%|████ | 4/10 [00:03<00:04, 1.35it/s]
Early stopping, best iteration is:
[677] training's rmse: 1.58701 valid_1's rmse: 29.5476
Training until validation scores don't improve for 100 rounds
50%|█████ | 5/10 [00:03<00:03, 1.46it/s]
Early stopping, best iteration is:
[572] training's rmse: 1.90926 valid_1's rmse: 22.9558
Training until validation scores don't improve for 100 rounds
60%|██████ | 6/10 [00:04<00:03, 1.24it/s]
Early stopping, best iteration is:
[1201] training's rmse: 0.331789 valid_1's rmse: 33.0541
Training until validation scores don't improve for 100 rounds
70%|███████ | 7/10 [00:05<00:02, 1.07it/s]
Early stopping, best iteration is:
[1292] training's rmse: 0.278446 valid_1's rmse: 36.915
Training until validation scores don't improve for 100 rounds
80%|████████ | 8/10 [00:06<00:01, 1.31it/s]
Early stopping, best iteration is:
[261] training's rmse: 3.74099 valid_1's rmse: 16.3203
Training until validation scores don't improve for 100 rounds
90%|█████████ | 9/10 [00:07<00:00, 1.20it/s]
Early stopping, best iteration is:
[991] training's rmse: 0.710558 valid_1's rmse: 36.1448
Training until validation scores don't improve for 100 rounds
100%|██████████| 10/10 [00:07<00:00, 1.31it/s]
100%|██████████| 10/10 [00:07<00:00, 1.26it/s]
Early stopping, best iteration is:
[636] training's rmse: 1.47725 valid_1's rmse: 22.2107
0%| | 0/10 [00:00<?, ?it/s]
Training until validation scores don't improve for 100 rounds
Early stopping, best iteration is:
[2524] training's rmse: 0.237055 valid_1's rmse: 33.2555
10%|█ | 1/10 [00:02<00:20, 2.24s/it]
Training until validation scores don't improve for 100 rounds
20%|██ | 2/10 [00:03<00:13, 1.72s/it]
Early stopping, best iteration is:
[1635] training's rmse: 0.713115 valid_1's rmse: 23.7664
Training until validation scores don't improve for 100 rounds
20%|██ | 2/10 [00:05<00:20, 2.56s/it]
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
Cell In[3], line 117
114 results.append(result)
116 params["quant_train_renew_leaf"] = True
--> 117 result = trials(name="量子化あり・Renewあり", params=params, n_trials=n_trials)
118 results.append(result)
Cell In[3], line 62, in trials(name, params, n_trials)
59 lgb_train, lgb_val, X_test, y_test = gen_dataset(seed=i)
61 t0 = time()
---> 62 model, _logs = train(params, lgb_train, lgb_val)
63 t1 = time()
64 train_times.append(t1 - t0)
Cell In[3], line 21, in train(params, lgb_train, lgb_val)
19 def train(params, lgb_train, lgb_val):
20 logs = {}
---> 21 model = lgb.train(
22 params,
23 lgb_train,
24 num_boost_round=100_000,
25 valid_sets=[lgb_train, lgb_val],
26 callbacks=[
27 lgb.early_stopping(stopping_rounds=100),
28 lgb.log_evaluation(period=100000),
29 lgb.record_evaluation(logs)
30 ]
31 )
32 return model, logs
File /usr/local/lib/python3.10/site-packages/lightgbm/engine.py:307, in train(params, train_set, num_boost_round, valid_sets, valid_names, feval, init_model, feature_name, categorical_feature, keep_training_booster, callbacks)
295 for cb in callbacks_before_iter:
296 cb(
297 callback.CallbackEnv(
298 model=booster,
(...)
304 )
305 )
--> 307 booster.update(fobj=fobj)
309 evaluation_result_list: List[_LGBM_BoosterEvalMethodResultType] = []
310 # check evaluation result.
File /usr/local/lib/python3.10/site-packages/lightgbm/basic.py:4136, in Booster.update(self, train_set, fobj)
4133 if self.__set_objective_to_none:
4134 raise LightGBMError("Cannot update due to null objective function.")
4135 _safe_call(
-> 4136 _LIB.LGBM_BoosterUpdateOneIter(
4137 self._handle,
4138 ctypes.byref(is_finished),
4139 )
4140 )
4141 self.__is_predicted_cur_iter = [False for _ in range(self.__num_dataset)]
4142 return is_finished.value == 1
KeyboardInterrupt:
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
res = pd.concat(results)
fig, axes = plt.subplots(figsize=[10, 8], nrows=2, ncols=2)
fig.subplots_adjust(hspace=0.3)
i, j = 0, 0
col = 'Training time'
sns.kdeplot(data=res, x=col, hue="条件", common_norm=False, ax=axes[i, j])
axes[i, j].set(title=f"{col}")
i, j = 0, 1
col = 'Inference time'
sns.kdeplot(data=res, x=col, hue="条件", common_norm=False, ax=axes[i, j])
axes[i, j].set(title=f"{col}")
i, j = 1, 0
col = 'RMSE'
sns.kdeplot(data=res, x=col, hue="条件", common_norm=False, ax=axes[i, j])
axes[i, j].set(title=f"{col}")
i, j = 1, 1
col = 'Model Size (MB)'
sns.kdeplot(data=res, x=col, hue="条件", common_norm=False, ax=axes[i, j])
axes[i, j].set(title=f"{col}")
fig.show()
