テイラー近似

平均値の定理

平均値の定理

関数 \(f(x)\) が \(a \leqq x \leqq b\) で連続で \(a<x<b\) で微分可能ならば、ある点 \(c(a<c<b)\) が存在して、

\[ f^{\prime}(c)=\frac{f(b)-f(a)}{b-a} \quad(a<c<b) \]

が成り立つ。

この定理は 直線 \(\mathrm{AB}\) と同じ傾きをもつ接線が弧 \(\mathrm{AB}\)上に存在することを意味している。

平均値の定理から分母を払って

\[ f(b) = f(a) + f'(c) (b - a) \]

としたものを一般化したのがテイラーの定理

テイラー展開

テイラーの定理

関数 \(f(x)\) が \(a \leqq x \leqq b\) で \(n\) 階まで連続な導関数をもち、 \(a<x<b\) で \(n+1\) 階微分可能ならば、ある点 \(c(a<c<b)\) が存在して、

\[\begin{split} \begin{aligned} f(b)= & f(a)+f^{\prime}(a)(b-a)+\frac{1}{2 !} f^{\prime \prime}(a)(b-a)^2+\cdots+\frac{1}{n !} f^{(n)}(a)(b-a)^n \\ & +\frac{1}{(n+1) !} f^{(n+1)}(c)(b-a)^{n+1} \quad(a<c<b) \end{aligned} \end{split}\]

が成り立つ。

\(n=0\)（1階微分可能）のとき、平均値の定理と一致する。

テイラーの定理の最後の項

\[ \frac{1}{(n+1) !} f^{(n+1)}(c)(b-a)^{n+1} \quad(a<c<b) \]

はラグランジュの剰余項と呼ばれる代表的な剰余項である。

\(c\)を\(c=a+\theta(b-a)(0<\theta<1)\)と書き、\(b = x\)とおけば、テイラー展開と呼ばれる式になる

テイラー展開

\[\begin{split} \begin{aligned} f(x)&=f(a)+f^{\prime}(a)(x-a)+\frac{1}{2 !} f^{\prime \prime}(a)(x-a)^2+\cdots+\frac{1}{n !} f^{(n)}(a)(x-a)^n+R_{n+1}\\ R_{n+1}&=\frac{1}{(n+1) !} f^{(n+1)}(a+\theta(x-a))(x-a)^{n+1} \quad(0<\theta<1) \end{aligned} \end{split}\]

これを関数\(f(x)\)の点\(a\)における テイラー展開（Taylor expansion） という。

テイラー級数

関数\(f(x)\)の点\(a\)におけるテイラー展開は有限個のベキ項と剰余\(R_{n+1}\)の和の形になる。

関数\(f(x)\)をより良く近似しようとすると、剰余\(R_{n+1}\)をより小さくする必要がある。

剰余\(R_n\)は\(n\)の値を増やしていくと、数列\(R_1, R_2, \cdots, R_n, \cdots\)を作る。もし、数列\(\{R_n\}\)が\(0\)に収束する、すなわち

\[ \lim_{n\to \infty} \{R_n\} = 0 \]

ならば、\(n\)を増やしてより多くの項で近似するほど、よりよい近似になる。

このとき、

\[ f(x)=f(a)+f^{\prime}(a)(x-a)+f^{\prime \prime}(a) \frac{(x-a)^2}{2 !}+\cdots+f^{(n)}(a) \frac{(x-a)^n}{n !}+\cdots \]

と書く。最後の\(\cdots\)は無限に和が続くことを意味している。これを テイラー級数 （Taylor series）と呼ぶ。

テイラー級数

\[\begin{split} \begin{align} f(x) &= f(a)+f^{\prime}(a)(x-a)+f^{\prime \prime}(a) \frac{(x-a)^2}{2 !}+\cdots+f^{(n)}(a) \frac{(x-a)^n}{n !}+\cdots\\ &= \sum_{n=0}^{\infty} \frac{ f^{(n)}(a)}{n!}(x-a)^n \end{align} \end{split}\]

例：対数変換による変化率の近似

定理：時系列分析における、対数差分系列（対数系列\(\log y_t\)の差分系列\(\Delta \log y_t = \log y_t - \log y_{t-1}\)）が十分小さい変化率の近似になる

\[ \log \left(y_t\right) - \log \left(y_{t-1}\right) \approx \frac{y_t-y_{t-1}}{y_{t-1}} \]

証明：対数の計算規則から

\[ \log \left(y_t\right) - \log \left(y_{t-1}\right) =\log \left(\frac{y_t}{y_{t-1}}\right) =\log \left(1+\frac{y_t-y_{t-1}}{y_{t-1}}\right) \]

となる。

またテイラー近似により

\[ \log(1 + x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots \]

となり、第2項以降は小さい\(x\)に対しては微小な値になるため

1次のテイラー近似

\[ \log(1 + x) \approx x \]

を利用して

\[ \log \left(1+\frac{y_t-y_{t-1}}{y_{t-1}}\right) \approx \frac{y_t-y_{t-1}}{y_{t-1}} \]

となる

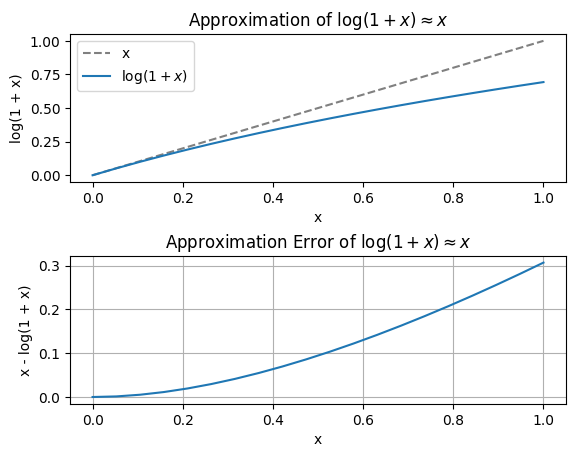
近似誤差について

\(\log(1+x) \approx x\)の近似誤差は\(x = 0.5\)くらいから0.1くらいになってくる

Show code cell source

Hide code cell source

# log(1 + x) \approx x の実験
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 1, 20)
approx = np.log(1 + x)

fig, axes = plt.subplots(nrows=2)
axes[0].plot(x, x, color="gray", linestyle="--", label="x")
axes[0].plot(x, approx, label=r"$\log(1 + x)$")
axes[0].legend()
axes[0].set(
    title=r"Approximation of $\log(1 + x) \approx x$",
    xlabel="x",
    ylabel="log(1 + x)"
)
fig.subplots_adjust(hspace=.5)

errors = x - approx
axes[1].plot(x, errors)
axes[1].set(
    title=r"Approximation Error of $\log(1 + x) \approx x$",
    xlabel="x",
    ylabel="x - log(1 + x)"
)
axes[1].grid(True)

fig.show()

例：対数変換した変数の回帰係数の解釈

これも同様に変化率の近似として解釈できる

マクローリン展開

テイラー展開の特別の場合として、\(a=0\)のときの場合を マクローリン展開 という。

マクローリン展開

\[\begin{split} \begin{aligned} f(x)= & f(0) + f^{\prime}(0)x + \frac{1}{2 !} f^{\prime \prime}(0) x^2 + \cdots + \frac{1}{n !} f^{(n)}(0) x^n \\ & + \frac{1}{(n+1) !} f^{(n+1)}(\theta x) x^{n+1} \quad(0<\theta<1) \end{aligned} \end{split}\]

例：指数関数

オイラーによる指数関数の定義

\[ \exp (x)=\lim _{n \rightarrow \infty}\left(1+\frac{x}{n}\right)^n \]

のマクローリン級数での表現は

\[ \exp (x)=\sum_{n=0}^{\infty} \frac{x^n}{n !}=1+x+\frac{x^2}{2 !}+\frac{x^3}{3 !}+\frac{x^4}{4 !}+\cdots \]

となる。こちらも指数関数の定義として扱われることがある。