点推定

点推定#

ある確率分布\(f(x|\boldsymbol{\theta})\)を想定し、その未知の母数\(\boldsymbol{\theta}=(\theta_1, ..., \theta_k)\)を、その確率分布に従うランダムに抽出した\(n\)個の標本\(\boldsymbol{X}=(X_1,...,X_n)\)にもとづいて推定する問題を考える。

モーメント法#

\[ X_1, ..., X_n, i.i.d. \sim f(x|\boldsymbol{\theta}) \]

のランダムサンプルについて、モーメント \(E[X^r]\) を標本モーメント \(\frac{1}{n} \sum^n_{i=1} X_i^r\) で置き換え

\[\begin{split} \begin{cases} \displaystyle \frac{1}{n} \sum^n_{i=1} X_i = \mu_1' (\theta_1, ..., \theta_k) \\ \displaystyle \frac{1}{n} \sum^n_{i=1} X_i^2 = \mu_2' (\theta_1, ..., \theta_k) \\ \vdots\\ \displaystyle \frac{1}{n} \sum^n_{i=1} X_i^k = \mu_k' (\theta_1, ..., \theta_k) \\ \end{cases} \end{split}\]

の同時方程式を\(\theta_1,...,\theta_k\)について解くことによって推定量\(\hat{\boldsymbol{\theta}}=(\hat{\theta}_1, ..., \hat{\theta}_k)\)を得る。これをモーメント推定量（moment estimator）という。

例

\(X \sim N(\mu, \sigma^2)\)とすると、

\[\begin{split} \begin{cases} \displaystyle \frac{1}{n} \sum^n_{i=1} X_i = \mu\\ \displaystyle \frac{1}{n} \sum^n_{i=1} X_i^2 = \sigma^2 + \mu^2 \end{cases} \end{split}\]

より、

\[\begin{split} \begin{align} \hat{\mu} &= \frac{1}{n} \sum^n_{i=1} X_i\\ \hat{\sigma}^2 &= \frac{1}{n} \sum^n_{i=1} (X_i - \hat{\mu})^2\\ \end{align} \end{split}\]

が\(\mu, \sigma^2\)のモーメント推定量となる。

最尤推定法#

「得られた標本は確率が最大のもの（最も尤もらしいもの）が実現した」という仮定に基づき、もっともらしさの関数（尤度関数）を最大にするパラメータを推定する方法。

尤度関数（likelihood function）とは\(X_1,...,X_n\)の確率関数の積

\[ L(\boldsymbol{\theta}|\boldsymbol{X}) = \prod^n_{i=1} f(X_i|\boldsymbol{\theta}) \]

で、サンプルのもとでその\(\theta\)のもっともらしさを示す関数である。

確率の積は数学的には扱いにくいので、通常はその対数をとった対数尤度

\[ \log L(\boldsymbol{\theta}|\boldsymbol{X}) = \sum^n_{i=1} \log f(X_i|\boldsymbol{\theta}) \]

を扱う。

例：コイントス

コインを5回投げて2回表がでた（表を1とすると、\(\boldsymbol{X}=(0,1,1,0,0)\)）とする。

確率\(p\)で1をとるベルヌーイ分布の確率質量関数は

\[ P(X=1) = p, P(X=0)= 1-p \]

であるため、尤度関数は

\[\begin{split} \begin{align} L(p|\boldsymbol{X}) &= (1-p) \times p \times p \times (1-p) \times (1-p)\\ &= p^2 (1-p)^{5-2} \end{align} \end{split}\]

となり、尤度関数にいれる\(p\)の値を変えていくと

\[\begin{split} \begin{align} L(p=0.1|\boldsymbol{X}) = 0.1^2 \times 0.9^3 = 0.00729\\ L(p=0.5|\boldsymbol{X}) = 0.5^2 \times 0.5^3 = 0.03125\\ L(p=0.9|\boldsymbol{X}) = 0.9^2 \times 0.1^3 = 0.00081 \end{align} \end{split}\]

のようになる。これを繰り返すと次の図のように描くことができる。

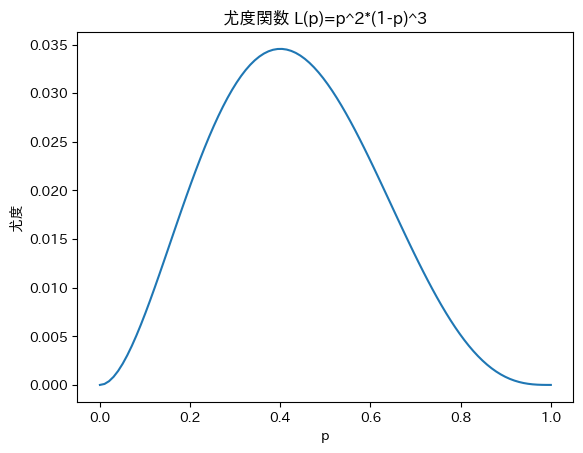
../../_images/edd1cfbaea264378cc0454b1689ebb1ae9d84b2aa050bbfe6e8145480deb0f01.png

そして、尤度関数を最大化するパラメータを点推定量として採用する。

Hide code cell source

 
# 尤度関数のプロットを描いたコード
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

x = np.array([0, 1, 1, 0, 0])

def bernoulli(p, r, n):
    return p ** r * (1 - p) ** (n - r)

theta = np.linspace(0, 1, 100)
likelihood = [bernoulli(p, r = sum(x), n = len(x)) for p in theta]


fig, ax = plt.subplots()
ax.plot(theta, likelihood)
ax.set(xlabel='p', ylabel='尤度', title='尤度関数 L(p)=p^2*(1-p)^3')

from myst_nb import glue
glue("cointoss_likelihood", fig, display=False)

Hide code cell output
../../_images/edd1cfbaea264378cc0454b1689ebb1ae9d84b2aa050bbfe6e8145480deb0f01.png

ベイズ法#

同時確率密度関数\(f(\boldsymbol{x}|\boldsymbol{\theta})\)の\(\boldsymbol{\theta}\)を確率変数とみなして確率分布を仮定する。これを事前分布（prior distribution）といい、\(\pi(\boldsymbol{\theta}|\boldsymbol{\xi})\)と書く。\(\boldsymbol{\xi}\)は事前分布の母数であり、超母数（hyperparameter）と呼ばれる。

このモデルは次のように表される。

\[\begin{split} \begin{cases} \boldsymbol{X}|\boldsymbol{\theta} \sim f(\boldsymbol{x}|\boldsymbol{\theta})\\ \boldsymbol{\theta} \sim \pi (\boldsymbol{\theta}|\boldsymbol{\xi}) \end{cases} \end{split}\]

\(\boldsymbol{X}=\boldsymbol{x}\)を与えたときの\(\boldsymbol{\theta}\)の条件付き分布を\(\boldsymbol{\theta}\)の事後分布（posterior distribution）といい、

\[ \displaystyle \pi(\boldsymbol{\theta | x, \xi}) = \frac{ f(\boldsymbol{x|\theta}) \pi(\boldsymbol{\theta|\xi}) } { f_\pi (\boldsymbol{x | \xi}) } \]

で与えられる。

ここで\(f_\pi (\boldsymbol{x | \xi})\)は\(\boldsymbol{X}\)の周辺分布で、\(\boldsymbol{\theta}\)が連続型確率変数のとき

\[ f_\pi (\boldsymbol{x | \xi}) = \int f(\boldsymbol{x|\theta}) \pi(\boldsymbol{\theta|\xi}) d \boldsymbol{\theta} \]

である。

ベイズ法とは事後分布から推定量を導く方法である。事後分布の平均\(E[\boldsymbol{\theta|X}]\)は事後期待値（expected a posteriori: EAP）と呼ばれる。 事後分布の最頻値は事後確率最大値（maximum a posteriori: MAP）やベイズ的最尤推定量（Bayesian maximum likelihood estimator）と呼ばれる。こうした分布の代表値を使用して点推定を行うことができる。

MCMCによる推定#

Hide code cell source

 
# nest_asyncio: asyncioを使うstanをjupyterで使うための対処
# [Stanによる推定例：ベルヌーイ分布のパラメータ - The One with ...](https://hamada.hatenablog.jp/entry/2017/06/28/100815)

import nest_asyncio
nest_asyncio.apply()

import stan


stan_code = """
data {
    int N;
    array[N] int X;
}
parameters {
    real<lower=0, upper=1> p;
}
model {
    for (i in 1:N) 
        X[i] ~ bernoulli(p);
}
"""

x = np.array([0, 1, 1, 0, 0])

data = {
    "N": len(x),
    "X": x,
}

posterior = stan.build(stan_code, data=data, random_seed=1)
fit = posterior.sample(num_chains=10, num_samples=10000)
df = fit.to_frame()
df

Hide code cell output

 
Building: 0.2s
Building: 0.3s
Building: 0.4s
Building: 0.5s
Building: 0.6s
Building: 0.7s
Building: 0.8s
Building: 0.9s
Building: 1.0s
Building: 1.1s
Building: 1.2s
Building: 1.3s
Building: 1.4s
Building: 1.6s
Building: 1.7s
Building: 1.8s
Building: 1.9s
Building: 2.0s
Building: 2.1s
Building: 2.2s
Building: 2.3s
Building: 2.4s
Building: 2.5s
Building: 2.6s
Building: 2.7s
Building: 2.8s
Building: 2.9s
Building: 3.0s
Building: 3.1s
Building: 3.2s
Building: 3.3s
Building: 3.4s
Building: 3.5s
Building: 3.6s
Building: 3.8s
Building: 3.9s
Building: 4.0s
Building: 4.1s
Building: 4.2s
Building: 4.3s
Building: 4.4s
Building: 4.5s
Building: 4.6s
Building: 4.7s
Building: 4.8s
Building: 4.9s
Building: 5.0s
Building: 5.1s
Building: 5.2s
Building: 5.3s
Building: 5.4s
Building: 5.5s
Building: 5.6s
Building: 5.7s
Building: 5.8s
Building: 5.9s
Building: 6.0s
Building: 6.2s
Building: 6.3s
Building: 6.4s
Building: 6.5s
Building: 6.6s
Building: 6.7s
Building: 6.8s
Building: 6.9s
Building: 7.0s
Building: 7.1s
Building: 7.2s
Building: 7.3s
Building: 7.4s
Building: 7.5s
Building: 7.6s
Building: 7.7s
Building: 7.8s
Building: 7.9s
Building: 8.0s
Building: 8.1s
Building: 8.2s
Building: 8.3s
Building: 8.5s
Building: 8.6s
Building: 8.7s
Building: 8.8s
Building: 8.9s
Building: 9.0s
Building: 9.1s
Building: 9.2s
Building: 9.3s
Building: 9.4s
Building: 9.5s
Building: 9.6s
Building: 9.7s
Building: 9.8s
Building: 9.9s
Building: 10.0s
Building: 10.1s
Building: 10.2s
Building: 10.3s
Building: 10.4s
Building: 10.5s
Building: 10.6s
Building: 10.8s
Building: 10.9s
Building: 11.0s
Building: 11.1s
Building: 11.2s
Building: 11.3s
Building: 11.4s
Building: 11.5s
Building: 11.6s
Building: 11.7s
Building: 11.8s
Building: 11.9s
Building: 12.0s
Building: 12.1s
Building: 12.2s
Building: 12.3s
Building: 12.4s
Building: 12.5s
Building: 12.6s
Building: 12.7s
Building: 12.8s
Building: 12.9s
Building: 13.1s
Building: 13.2s
Building: 13.3s
Building: 13.4s
Building: 13.5s

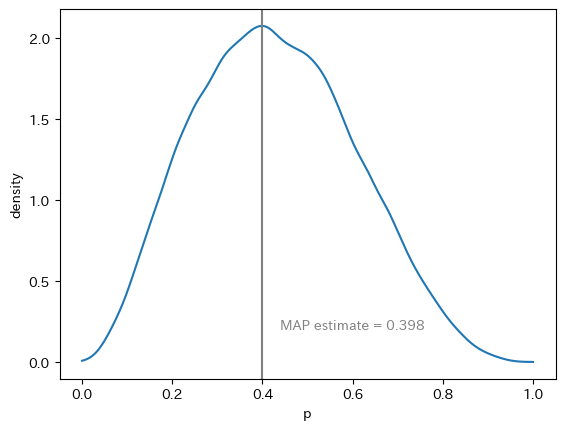
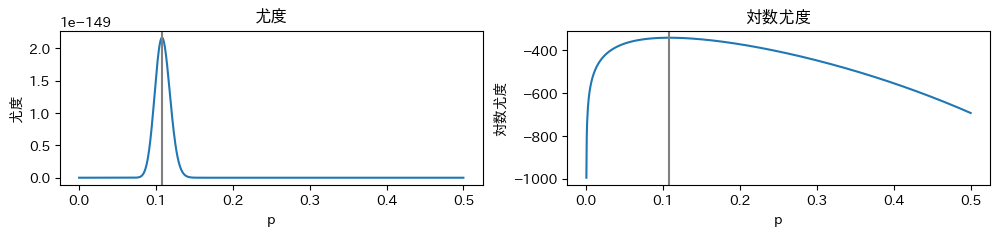
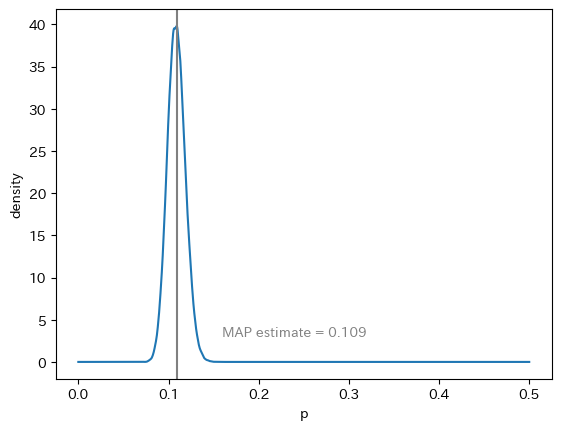
In file included from /usr/local/lib/python3.9/site-packages/httpstan/include/boost/multi_array/multi_array_ref.hpp:32,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/boost/multi_array.hpp:34,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/boost/numeric/odeint/algebra/multi_array_algebra.hpp:22,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/boost/numeric/odeint.hpp:63,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/stan/math/prim/functor/ode_rk45.hpp:9,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/stan/math/prim/functor/integrate_ode_rk45.hpp:6,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/stan/math/prim/functor.hpp:14,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/stan/math/rev/fun.hpp:196,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/stan/math/rev.hpp:10,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/stan/math.hpp:19,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/stan/model/model_header.hpp:4,
                 from /root/.cache/httpstan/4.8.2/models/5zjucfky/model_5zjucfky.cpp:2:
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:180:45: warning: ‘template<class _Arg, class _Result> struct std::unary_function’ is deprecated [-Wdeprecated-declarations]
  180 |         : public boost::functional::detail::unary_function<typename unary_traits<Predicate>::argument_type,bool>
      |                                             ^~~~~~~~~~~~~~
In file included from /usr/include/c++/12/string:48,
                 from /usr/include/c++/12/bits/locale_classes.h:40,
                 from /usr/include/c++/12/bits/ios_base.h:41,
                 from /usr/include/c++/12/ios:42,
                 from /usr/include/c++/12/istream:38,
                 from /usr/include/c++/12/sstream:38,
                 from /usr/include/c++/12/complex:45,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/Eigen/Core:96,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/Eigen/Dense:1,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/stan/math/prim/fun/Eigen.hpp:22,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/stan/math/rev.hpp:4:
/usr/include/c++/12/bits/stl_function.h:117:12: note: declared here
  117 |     struct unary_function
      |            ^~~~~~~~~~~~~~
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:214:45: warning: ‘template<class _Arg1, class _Arg2, class _Result> struct std::binary_function’ is deprecated [-Wdeprecated-declarations]
  214 |         : public boost::functional::detail::binary_function<
      |                                             ^~~~~~~~~~~~~~~
/usr/include/c++/12/bits/stl_function.h:131:12: note: declared here
  131 |     struct binary_function
      |            ^~~~~~~~~~~~~~~
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:252:45: warning: ‘template<class _Arg, class _Result> struct std::unary_function’ is deprecated [-Wdeprecated-declarations]
  252 |         : public boost::functional::detail::unary_function<
      |                                             ^~~~~~~~~~~~~~
/usr/include/c++/12/bits/stl_function.h:117:12: note: declared here
  117 |     struct unary_function
      |            ^~~~~~~~~~~~~~
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:299:45: warning: ‘template<class _Arg, class _Result> struct std::unary_function’ is deprecated [-Wdeprecated-declarations]
  299 |         : public boost::functional::detail::unary_function<
      |                                             ^~~~~~~~~~~~~~
/usr/include/c++/12/bits/stl_function.h:117:12: note: declared here
  117 |     struct unary_function
      |            ^~~~~~~~~~~~~~
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:345:57: warning: ‘template<class _Arg, class _Result> struct std::unary_function’ is deprecated [-Wdeprecated-declarations]
  345 |     class mem_fun_t : public boost::functional::detail::unary_function<T*, S>
      |                                                         ^~~~~~~~~~~~~~
/usr/include/c++/12/bits/stl_function.h:117:12: note: declared here
  117 |     struct unary_function
      |            ^~~~~~~~~~~~~~
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:361:58: warning: ‘template<class _Arg1, class _Arg2, class _Result> struct std::binary_function’ is deprecated [-Wdeprecated-declarations]
  361 |     class mem_fun1_t : public boost::functional::detail::binary_function<T*, A, S>
      |                                                          ^~~~~~~~~~~~~~~
/usr/include/c++/12/bits/stl_function.h:131:12: note: declared here
  131 |     struct binary_function
      |            ^~~~~~~~~~~~~~~
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:377:63: warning: ‘template<class _Arg, class _Result> struct std::unary_function’ is deprecated [-Wdeprecated-declarations]
  377 |     class const_mem_fun_t : public boost::functional::detail::unary_function<const T*, S>
      |                                                               ^~~~~~~~~~~~~~
/usr/include/c++/12/bits/stl_function.h:117:12: note: declared here
  117 |     struct unary_function
      |            ^~~~~~~~~~~~~~
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:393:64: warning: ‘template<class _Arg1, class _Arg2, class _Result> struct std::binary_function’ is deprecated [-Wdeprecated-declarations]
  393 |     class const_mem_fun1_t : public boost::functional::detail::binary_function<const T*, A, S>
      |                                                                ^~~~~~~~~~~~~~~
/usr/include/c++/12/bits/stl_function.h:131:12: note: declared here
  131 |     struct binary_function
      |            ^~~~~~~~~~~~~~~
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:438:61: warning: ‘template<class _Arg, class _Result> struct std::unary_function’ is deprecated [-Wdeprecated-declarations]
  438 |     class mem_fun_ref_t : public boost::functional::detail::unary_function<T&, S>
      |                                                             ^~~~~~~~~~~~~~
/usr/include/c++/12/bits/stl_function.h:117:12: note: declared here
  117 |     struct unary_function
      |            ^~~~~~~~~~~~~~
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:454:62: warning: ‘template<class _Arg1, class _Arg2, class _Result> struct std::binary_function’ is deprecated [-Wdeprecated-declarations]
  454 |     class mem_fun1_ref_t : public boost::functional::detail::binary_function<T&, A, S>
      |                                                              ^~~~~~~~~~~~~~~
/usr/include/c++/12/bits/stl_function.h:131:12: note: declared here
  131 |     struct binary_function
      |            ^~~~~~~~~~~~~~~
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:470:67: warning: ‘template<class _Arg, class _Result> struct std::unary_function’ is deprecated [-Wdeprecated-declarations]
  470 |     class const_mem_fun_ref_t : public boost::functional::detail::unary_function<const T&, S>
      |                                                                   ^~~~~~~~~~~~~~
/usr/include/c++/12/bits/stl_function.h:117:12: note: declared here
  117 |     struct unary_function
      |            ^~~~~~~~~~~~~~
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:487:68: warning: ‘template<class _Arg1, class _Arg2, class _Result> struct std::binary_function’ is deprecated [-Wdeprecated-declarations]
  487 |     class const_mem_fun1_ref_t : public boost::functional::detail::binary_function<const T&, A, S>
      |                                                                    ^~~~~~~~~~~~~~~
/usr/include/c++/12/bits/stl_function.h:131:12: note: declared here
  131 |     struct binary_function
      |            ^~~~~~~~~~~~~~~
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:533:73: warning: ‘template<class _Arg, class _Result> struct std::unary_function’ is deprecated [-Wdeprecated-declarations]
  533 |     class pointer_to_unary_function : public boost::functional::detail::unary_function<Arg,Result>
      |                                                                         ^~~~~~~~~~~~~~
/usr/include/c++/12/bits/stl_function.h:117:12: note: declared here
  117 |     struct unary_function
      |            ^~~~~~~~~~~~~~
/usr/local/lib/python3.9/site-packages/httpstan/include/boost/functional.hpp:557:74: warning: ‘template<class _Arg1, class _Arg2, class _Result> struct std::binary_function’ is deprecated [-Wdeprecated-declarations]
  557 |     class pointer_to_binary_function : public boost::functional::detail::binary_function<Arg1,Arg2,Result>
      |                                                                          ^~~~~~~~~~~~~~~
/usr/include/c++/12/bits/stl_function.h:131:12: note: declared here
  131 |     struct binary_function
      |            ^~~~~~~~~~~~~~~

Building: 13.6s
Building: 13.7s
Building: 13.8s
Building: 13.9s
Building: 14.0s
Building: 14.1s
Building: 14.2s
Building: 14.3s
Building: 14.4s
Building: 14.5s
Building: 14.6s
Building: 14.7s
Building: 14.8s
Building: 14.9s
Building: 15.0s
Building: 15.1s
Building: 15.2s
Building: 15.4s
Building: 15.5s
Building: 15.6s
Building: 15.7s
Building: 15.8s
Building: 15.9s
Building: 16.0s
Building: 16.1s
Building: 16.2s
Building: 16.3s

In file included from /usr/local/lib/python3.9/site-packages/httpstan/include/stan/model/indexing.hpp:5,
                 from /usr/local/lib/python3.9/site-packages/httpstan/include/stan/model/model_header.hpp:17:
/usr/local/lib/python3.9/site-packages/httpstan/include/stan/model/indexing/assign_varmat.hpp: In function ‘void stan::model::assign(Mat1&&, const Mat2&, const char*, const index_multi&, const index_multi&)’:
/usr/local/lib/python3.9/site-packages/httpstan/include/stan/model/indexing/assign_varmat.hpp:401:9: warning: typedef ‘using pair_type = struct std::pair<int, std::vector<int, stan::math::arena_allocator<int> > >’ locally defined but not used [-Wunused-local-typedefs]
  401 |   using pair_type = std::pair<int, arena_vec>;
      |         ^~~~~~~~~
/root/.cache/httpstan/4.8.2/models/5zjucfky/model_5zjucfky.cpp: In constructor ‘model_5zjucfky_namespace::model_5zjucfky::model_5zjucfky(stan::io::var_context&, unsigned int, std::ostream*)’:
/root/.cache/httpstan/4.8.2/models/5zjucfky/model_5zjucfky.cpp:52:11: warning: variable ‘pos__’ set but not used [-Wunused-but-set-variable]
   52 |       int pos__ = std::numeric_limits<int>::min();
      |           ^~~~~

Building: 16.4s
Building: 16.5s
Building: 16.6s
Building: 16.7s
Building: 16.8s
Building: 16.9s
Building: 17.0s
Building: 17.1s

/root/.cache/httpstan/4.8.2/models/5zjucfky/model_5zjucfky.cpp: In instantiation of ‘void model_5zjucfky_namespace::model_5zjucfky::transform_inits_impl(VecVar&, VecI&, VecVar&, std::ostream*) const [with VecVar = std::vector<double, std::allocator<double> >; VecI = std::vector<int>; stan::require_vector_t<T_y>* <anonymous> = 0; stan::require_vector_like_vt<std::is_integral, VecI>* <anonymous> = 0; std::ostream = std::basic_ostream<char>]’:
/root/.cache/httpstan/4.8.2/models/5zjucfky/model_5zjucfky.cpp:326:26:   required from here
/root/.cache/httpstan/4.8.2/models/5zjucfky/model_5zjucfky.cpp:173:11: warning: variable ‘pos__’ set but not used [-Wunused-but-set-variable]
  173 |       int pos__ = std::numeric_limits<int>::min();
      |           ^~~~~

Building: 17.2s
Building: 17.3s
Building: 17.4s
Building: 17.5s
Building: 17.7s
Building: 17.8s
Building: 17.9s
Building: 18.0s
Building: 18.1s
Building: 18.2s
Building: 18.3s
Building: 18.4s
Building: 18.5s
Building: 18.6s
Building: 18.7s
Building: 18.8s
Building: 18.9s
Building: 19.0s
Building: 19.1s
Building: 19.2s
Building: 19.3s
Building: 19.4s
Building: 19.5s
Building: 19.6s
Building: 19.7s
Building: 19.8s
Building: 19.9s
Building: 20.1s
Building: 20.2s
Building: 20.3s
Building: 20.4s
Building: 20.5s
Building: 20.6s
Building: 20.7s
Building: 20.8s
Building: 20.9s
Building: 21.0s
Building: 21.1s
Building: 21.2s
Building: 21.3s
Building: 21.4s
Building: 21.5s
Building: 21.6s
Building: 21.7s
Building: 21.8s
Building: 21.9s
Building: 22.0s
Building: 22.1s
Building: 22.2s
Building: 22.4s
Building: 22.5s
Building: 22.6s
Building: 22.7s
Building: 22.8s
Building: 22.9s
Building: 23.0s
Building: 23.1s
Building: 23.2s
Building: 23.3s
Building: 23.4s
Building: 23.5s
Building: 23.6s
Building: 23.7s
Building: 23.8s
Building: 23.9s
Building: 24.0s
Building: 24.1s
Building: 24.2s
Building: 24.3s
Building: 24.4s
Building: 24.5s
Building: 24.7s
Building: 24.8s
Building: 24.9s
Building: 25.0s
Building: 25.1s
Building: 25.2s
Building: 25.3s
Building: 25.4s
Building: 25.5s
Building: 25.6s
Building: 25.7s
Building: 25.8s
Building: 25.9s
Building: 26.0s
Building: 26.1s
Building: 26.2s
Building: 26.3s
Building: 26.4s
Building: 26.5s
Building: 26.6s
Building: 26.7s
Building: 26.8s
Building: 26.9s
Building: 27.1s
Building: 27.2s
Building: 27.3s
Building: 27.4s
Building: 27.5s
Building: 27.6s
Building: 27.7s
Building: 27.8s
Building: 27.9s
Building: 28.0s
Building: 28.1s
Building: 28.2s
Building: 28.3s
Building: 28.4s
Building: 28.5s
Building: 28.6s
Building: 28.7s
Building: 28.8s
Building: 28.9s
Building: 29.0s
Building: 29.1s
Building: 29.2s
Building: 29.4s
Building: 29.5s
Building: 29.6s
Building: 29.7s
Building: 29.8s
Building: 29.9s
Building: 30.0s


Building: 30.0s, done.
Messages from stanc:
Warning: The parameter p has no priors. This means either no prior is
    provided, or the prior(s) depend on data variables. In the later case,
    this may be a false positive.
Sampling:   0%
Sampling:  10% (11000/110000)
Sampling:  20% (22000/110000)
Sampling:  30% (33000/110000)
Sampling:  40% (44000/110000)
Sampling:  50% (55000/110000)
Sampling:  60% (66000/110000)
Sampling:  70% (77000/110000)
Sampling:  80% (88000/110000)
Sampling:  90% (99000/110000)
Sampling: 100% (110000/110000)
Sampling: 100% (110000/110000), done.
Messages received during sampling:
  Gradient evaluation took 1e-05 seconds
  1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 1.2e-05 seconds
  1000 transitions using 10 leapfrog steps per transition would take 0.12 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 1.1e-05 seconds
  1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 9e-06 seconds
  1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 9e-06 seconds
  1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 0.000129 seconds
  1000 transitions using 10 leapfrog steps per transition would take 1.29 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 1.1e-05 seconds
  1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 9e-06 seconds
  1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 1.5e-05 seconds
  1000 transitions using 10 leapfrog steps per transition would take 0.15 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 9e-06 seconds
  1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds.
  Adjust your expectations accordingly!
parameters lp__ accept_stat__ stepsize__ treedepth__ n_leapfrog__ divergent__ energy__ p
draws
0 -5.642715 0.858490 0.844098 1.0 3.0 0.0 5.727999 0.670866
1 -4.881275 0.989540 0.943361 1.0 3.0 0.0 5.861898 0.346497
2 -4.780382 0.981418 1.283229 2.0 3.0 0.0 5.292580 0.427244
3 -5.275625 0.868117 0.935121 1.0 3.0 0.0 5.452545 0.255209
4 -4.792388 0.998572 0.814226 2.0 3.0 0.0 4.885668 0.457724
... ... ... ... ... ... ... ... ...
99995 -4.785516 1.000000 1.154637 1.0 3.0 0.0 6.328481 0.447636
99996 -4.789597 1.000000 0.976298 1.0 3.0 0.0 4.925209 0.403287
99997 -5.225165 0.999028 0.934847 2.0 3.0 0.0 5.320427 0.605407
99998 -5.048547 1.000000 1.030901 1.0 1.0 0.0 5.673003 0.566566
99999 -5.654453 0.661121 0.959207 1.0 1.0 0.0 6.953122 0.672387

100000 rows × 8 columns

MCMCで生成した乱数の分布は次のようになった

Hide code cell source

 
import matplotlib.pyplot as plt
import seaborn as sns

burn_in = 10000
ax = sns.displot(x="p", data=df.iloc[burn_in:, :], kde=True, bins=20)

Hide code cell output
../../_images/8a6d98da6fb530db1842e5ca4cc4ffdf31d11d468427067a08a77e763d415f9f.png

Hide code cell source

 
# カーネル密度推定によりMAP推定値を取得する
from scipy.stats import gaussian_kde

kernel = gaussian_kde(df.iloc[burn_in:, :]["p"])

x_values = np.linspace(0, 1, 1000)
estimated_density = kernel(x_values)

max_index = np.argmax(estimated_density)
max_a_posteriori = x_values[max_index]  # MAP estimate

fig, ax = plt.subplots()
ax.plot(x_values, estimated_density)
ax.set(xlabel="p", ylabel="density")
ax.axvline(max_a_posteriori, color="gray")
ax.text(max_a_posteriori * 1.1, 0.2, f"MAP estimate = {max_a_posteriori:.3f}", color="gray")
fig.show()
../../_images/b04de5c86126e9f94e0316dd9e3c27c6dc3c692a935b217ecf210c88253f2f30.png

例#

あるゲームのガチャを1000回引いた結果、「外れ」と「当たり」の回数が以下のようになった。このガチャの「当たり」の確率はいくつか。

Hide code cell source

 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

np.random.seed(0)
x = np.random.binomial(n=1, p=0.1, size=1000)
x = pd.Series(x)

table = x.map({0: "外れ", 1: "当たり"}).value_counts().to_frame()
table.columns = ['回数']
table.T
外れ 当たり
回数 892 108

モーメント法による推定#

ベルヌーイ分布\(Ber(p)\)の平均が成功確率\(p\)なので、\(\hat{p} = \sum^n_{i=1} X_i / n\)

# モーメント法による推定
n = len(x)
sum(x) / n

0.108

最尤法による推定#

ベルヌーイ分布

\(X_i = 1\)となる確率が\(p\)のベルヌーイ分布\(Ber(p)\)に従った確率変数の実現値がサンプルだとしたとき、\(r=\sum X_i\)とすると、その尤度関数は

\[ L(p|X) = p^r (1-p)^{n-r} \]

であり、対数尤度関数は

\[ \log L(p|X) = r \log p + (n-r) \log (1-p) \]

となる。

今回のサンプルのもとでは次の図のような曲線になる。（グレーの縦線は最尤推定値のpを示す）

Hide code cell source

 
fig, axes = plt.subplots(ncols=2, figsize=(12, 2))

# 尤度関数
p_candidates = np.linspace(0.0001, 0.5, 1000)
likelihood = np.array([bernoulli(p, n = len(x), r = sum(x)) for p in p_candidates])
max_p = p_candidates[np.argmax(likelihood)]  # 最尤推定値

axes[0].plot(p_candidates, likelihood)
axes[0].set(xlabel='p', ylabel='尤度', title='尤度')
axes[0].axvline(max_p, color="gray")


# 対数尤度関数
def log_bernoulli(p, n, r):
    return r * np.log(p) + (n - r) * np.log(1 - p)

likelihood = np.array([log_bernoulli(p, n = len(x), r = sum(x)) for p in p_candidates])
max_p = p_candidates[np.argmax(likelihood)]  # 最尤推定値

axes[1].plot(p_candidates, likelihood)
axes[1].set(xlabel='p', ylabel='対数尤度', title='対数尤度')
axes[1].axvline(max_p, color="gray")

fig.show()
../../_images/3cd83934d9bcca52e98726854232867ca4ccc049a6be2031157f44821eb663c9.png

対数尤度の導関数は

\[ \frac{\partial \log L(p|X)}{\partial p} = \frac{r}{p} - \frac{n-r}{1-p} \]

で、これを0とおいて\(p\)について解くと

\[ p = \frac{r}{n} = \frac{\sum X_i}{n} \]

となり、モーメント法と同じ結果になる。

（参考）式展開

\[ \frac{\partial \log L(p|X)}{\partial p} = \frac{r}{p} - \frac{n-r}{1-p} = 0 \]

なので

\[ \frac{r}{p} = \frac{n-r}{1-p} \]

から

\[ \frac{p}{1-p} = \frac{r}{n-r} \]

なので

\[ p = \frac{r(1-p)}{n-r} = \frac{r(1-p)}{r(\frac{n}{r} - 1)} = \frac{1-p}{\frac{n}{r} - 1} \]

これは

\[ p (\frac{n}{r} - 1) = 1 - p \]

なので

\[ p \frac{n}{r} = 1 \]

ゆえに

\[ p = \frac{r}{n} = \frac{\sum X_i}{n} \]

解析的に解くことができない場合は勾配降下法などで数値的に解く。

ベイズ推定#

ベイズ推定ではパラメータの確率分布を推定するため、点推定を行いたい場合はその分布の何らかの代表値（期待値や中央値や最頻値）を推定することになる。

以下ではStanを用い、無情報事前分布を使用して推定を行う。

参考資料

# nest_asyncio: asyncioを使うstanをjupyterで使うための対処
# [Stanによる推定例：ベルヌーイ分布のパラメータ - The One with ...](https://hamada.hatenablog.jp/entry/2017/06/28/100815)
import nest_asyncio
nest_asyncio.apply()

import stan


stan_code = """
data {
    int N;
    array[N] int X;
}
parameters {
    real<lower=0, upper=1> p;
}
model {
    for (i in 1:N) 
        X[i] ~ bernoulli(p);
}
"""

data = {
    "N": len(x),
    "X": list(x),
}

posterior = stan.build(stan_code, data=data, random_seed=1)
fit = posterior.sample(num_chains=10, num_samples=10000)
df = fit.to_frame()

Hide code cell source

 
# nest_asyncio: asyncioを使うstanをjupyterで使うための対処
# [Stanによる推定例：ベルヌーイ分布のパラメータ - The One with ...](https://hamada.hatenablog.jp/entry/2017/06/28/100815)
import nest_asyncio
nest_asyncio.apply()

import stan


stan_code = """
data {
    int N;
    array[N] int X;
}
parameters {
    real<lower=0, upper=1> p;
}
model {
    for (i in 1:N) 
        X[i] ~ bernoulli(p);
}
"""

data = {
    "N": len(x),
    "X": list(x),
}

posterior = stan.build(stan_code, data=data, random_seed=1)
fit = posterior.sample(num_chains=10, num_samples=10000)
df = fit.to_frame()
df

Hide code cell output

 
Building: found in cache, done.
Messages from stanc:
Warning: The parameter p has no priors. This means either no prior is
    provided, or the prior(s) depend on data variables. In the later case,
    this may be a false positive.
Sampling:   0%
Sampling:  10% (11000/110000)
Sampling:  20% (22000/110000)
Sampling:  30% (33000/110000)
Sampling:  40% (44000/110000)
Sampling:  50% (55000/110000)
Sampling:  60% (66000/110000)
Sampling:  70% (77000/110000)
Sampling:  80% (88000/110000)
Sampling:  90% (99000/110000)
Sampling: 100% (110000/110000)
Sampling: 100% (110000/110000), done.
Messages received during sampling:
  Gradient evaluation took 0.000122 seconds
  1000 transitions using 10 leapfrog steps per transition would take 1.22 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 0.000118 seconds
  1000 transitions using 10 leapfrog steps per transition would take 1.18 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 0.000151 seconds
  1000 transitions using 10 leapfrog steps per transition would take 1.51 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 0.000118 seconds
  1000 transitions using 10 leapfrog steps per transition would take 1.18 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 0.00012 seconds
  1000 transitions using 10 leapfrog steps per transition would take 1.2 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 0.000127 seconds
  1000 transitions using 10 leapfrog steps per transition would take 1.27 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 0.000114 seconds
  1000 transitions using 10 leapfrog steps per transition would take 1.14 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 0.000112 seconds
  1000 transitions using 10 leapfrog steps per transition would take 1.12 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 0.000115 seconds
  1000 transitions using 10 leapfrog steps per transition would take 1.15 seconds.
  Adjust your expectations accordingly!
  Gradient evaluation took 0.000129 seconds
  1000 transitions using 10 leapfrog steps per transition would take 1.29 seconds.
  Adjust your expectations accordingly!
parameters lp__ accept_stat__ stepsize__ treedepth__ n_leapfrog__ divergent__ energy__ p
draws
0 -345.200821 1.000000 0.981903 1.0 1.0 0.0 346.792427 0.119392
1 -345.506862 0.950502 1.152834 2.0 3.0 0.0 345.508004 0.122103
2 -344.659955 0.972768 1.096480 2.0 3.0 0.0 345.061099 0.107403
3 -345.742589 0.855597 0.845899 2.0 3.0 0.0 346.189082 0.123889
4 -344.709336 1.000000 0.888807 1.0 1.0 0.0 344.734546 0.105426
... ... ... ... ... ... ... ... ...
99995 -345.266657 0.837712 0.965921 1.0 3.0 0.0 345.707968 0.098181
99996 -345.031246 0.699019 0.960980 1.0 3.0 0.0 347.278833 0.117569
99997 -345.580391 0.922817 0.935322 1.0 1.0 0.0 345.596114 0.095851
99998 -344.724189 0.993795 1.077615 1.0 1.0 0.0 344.735718 0.112609
99999 -344.693695 1.000000 0.956261 1.0 3.0 0.0 347.284101 0.105899

100000 rows × 8 columns

# カーネル密度推定によりMAP推定値を取得する
from scipy.stats import gaussian_kde

kernel = gaussian_kde(df.iloc[burn_in:, :]["p"])

x_values = np.linspace(0, 0.5, 1000)
estimated_density = kernel(x_values)

max_index = np.argmax(estimated_density)
max_a_posteriori = x_values[max_index]  # MAP estimate

fig, ax = plt.subplots()
ax.plot(x_values, estimated_density)
ax.set(xlabel="p", ylabel="density")
ax.axvline(max_a_posteriori, color="gray")
ax.text(max_a_posteriori + 0.05, 3, f"MAP estimate = {max_a_posteriori:.3f}", color="gray")
fig.show()
../../_images/ff27fbd1f070bb12940dd3b1a969cdb205068acc4d8bb83c2b3dd8ec9734c01e.png
Contents