Ctrl+K

定積分

定積分#

関数\(y=f(x)\)のグラフを考える。\(f(x)\)は区間\(a\leq x \leq b\)で連続であり正であるとする。その曲線、\(x=a, x=b\)で囲まれた面積を\(S\)とする

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 7, 300)
y = 0.5 * x + np.sin(x)
xticks = []
xticklabels = []

fig, ax = plt.subplots(figsize=[5,3])
ax.plot(x, y)

a = 1
ax.axvline(a, linestyle="--")
xticks.append(a)
xticklabels.append("$a$")

b = 6
ax.axvline(b, linestyle="--")
xticks.append(b)
xticklabels.append("$b$")

ax.set(xlabel="x", ylabel="y", xticks=xticks, xticklabels=xticklabels, yticks=[])
ax.fill_between(x[(a <= x) & (x <= b)], y[(a <= x) & (x <= b)], color='lightblue', alpha=0.5)
ax.text(a + 0.4 + (b - a) // 2, 0.5, "S", color="steelblue")

ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')

fig.show()
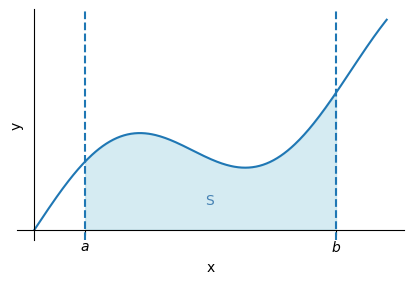
../../../_images/03a51cc82c179ae12d1188e48428133be6c9fc379310e570e2c1373a3bcdde0a.png

区間\(a\leq x \leq b\)を

\[ a=x_0<x_1<x_2<\cdots<x_{k-1}<x_k<\cdots<x_{n-1}<b=x_n \]

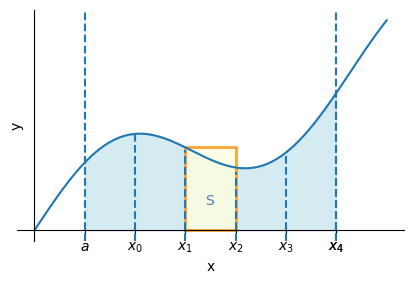
であるような\(n+1\)個の点\(x_0, x_1, x_2, \cdots, x_{n-1}, x_n\)によって\(n\)個の小区間\(I_1, I_2, \cdots, I_{n-1}, I_n\)に分割する。小区間\(I_k\)の大きさは\(\Delta x_k = x_k - x_{k-1}\)である。

点\(x_k\)に\(x\)軸に垂直な直線をひくと、面積\(S\)は\(n\)個の「帯」に分けられる。 小区間の中の点を\(\xi_k\)とすると、「帯」の面積は底辺の長さが\(\Delta x_k\)で高さが\(y_k=f(\xi_k)\)の長方形の面積\(f(\xi_k)\Delta x_k\)で近似する。

このとき、求める面積\(S\)は長方形の面積の和

\[ S_n = \sum^n_{k=1} f(\xi_k)\Delta x_k \]

で近似される。このような和を積和と呼ぶことにする。

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt

def f(x):
    return 0.5 * x + np.sin(x)

x = np.linspace(0, 7, 300)
y = f(x)
xticks = []
xticklabels = []

fig, ax = plt.subplots(figsize=[5,3])
ax.plot(x, y)

a = 1
ax.axvline(a, linestyle="--")
xticks.append(a)
xticklabels.append("$a$")

b = 6
ax.axvline(b, linestyle="--")
xticks.append(b)
xticklabels.append("$b$")

ax.fill_between(x[(a <= x) & (x <= b)], y[(a <= x) & (x <= b)], color='lightblue', alpha=0.5)
ax.text(a + 0.4 + (b - a) // 2, 0.5, "S", color="steelblue")

# 「帯」
x_ks = [a + i for i in range(1, b)]
for k, x_k in enumerate(x_ks):
    ax.axvline(x_k, ymax=f(x_k) / max(y), linestyle="--")
    xticks.append(x_k)
    xticklabels.append(f"$x_{k}$")

# 長方形
import matplotlib.patches as patches
linesettings = dict(color="darkorange", alpha=0.7)
delta_x = x_ks[2] - x_ks[1]
rect = patches.Rectangle(
    xy=(x_ks[1], 0),
    width=delta_x,
    height=f(x_ks[1]),
    linewidth=2,
    edgecolor='darkorange',
    facecolor='lightyellow',
    alpha=0.8
)
ax.add_patch(rect)

# axis
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')

ax.set(xlabel="x", ylabel="y", xticks=xticks, xticklabels=xticklabels, yticks=[])
fig.show()
../../../_images/ef5ba611051b10b4a09b74ed0d9dcd0ede52083b1ecc1a160fd16e5083b9f040.png

分割する小区間の長さ\(\Delta_x\)が限りなく小さくなるように細かく分割していくと、積和はある一定の値に限りなく近づく。その極限値（\(f(x)\)が連続なら必ず存在する）は面積\(S\)に等しい。

この極限値を

\[ \int_a^b f(x) d x=\lim _{n \rightarrow \infty} \sum_{k=1}^n f\left(\xi_k\right) \Delta x_k \]

で表し、関数\(f(x)\)の\(a\)から\(b\)までの 定積分 （definite integral） という。\(b\)を積分上限、\(a\)を積分下限と呼ぶ。

負の面積#

関数が負の場合をとる場合でも積分は定義できる。積和の定義より、関数の値が負の部分はその部分からの面積への寄与は負である。

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 7, 300)
y = np.sin(x - 0.5)
xticks = []
xticklabels = []

fig, ax = plt.subplots(figsize=[5,3])
ax.plot(x, y)

a = 1
ax.axvline(a, linestyle="--")
xticks.append(a)
xticklabels.append("$a$     ")

b = 6
ax.axvline(b, linestyle="--")
xticks.append(b)
xticklabels.append("$b$     ")

ax.set(xlabel="x", ylabel="y", xticks=xticks, xticklabels=xticklabels, yticks=[])
ax.fill_between(x[(a <= x) & (x <= b)], y[(a <= x) & (x <= b)], color='lightblue', alpha=0.5)

ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')

fig.show()
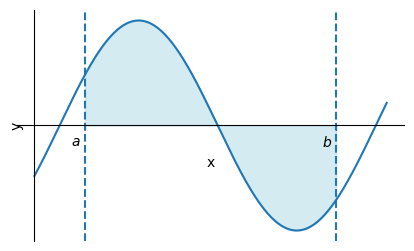
../../../_images/d611805af833da2f19560bf08bc26da25b34177a2d44df996648944c09074f0e.png

定積分の性質#

  1. \(\displaystyle \int_a^b\{f(x) \pm g(x)\} d x=\int_a^b f(x) d x \pm \int_a^b g(x) d x\)

  2. \(\displaystyle \int_a^b k f(x) d x=k \int_a^b f(x) d x \quad(k\) : 定数 \()\)

  3. \(\displaystyle a \leqq x \leqq b\) で \(f(x) \geqq 0\) ならば \(\int_a^b f(x) d x \geqq 0\)

  4. \(\displaystyle \quad a \leqq x \leqq b\) で \(f(x) \geqq g(x)\) ならば \(\int_a^b f(x) d x \geqq \int_a^b g(x) d x\)

  5. 平均値の定理：\(\displaystyle \int_a^b f(x) d x=f(c)(b-a) \quad(a<c<b)\)

定積分の計算#

\(F'(x) = f(x)\)を満たすある関数\(F(x)\)がわかったとき、定積分

\[ \int_a^b f(x) d x \]

はどのように求められるか。

下限を定数、上限を変数とした\(\int_a^x f(t) d t\)も原始関数であるから、

\[ \int_a^x f(t) d t = F(x) + C \]

が成り立つ。

上の式で\(x=a\)とおくと

\[ 0 = F(a) + C \]

なので

\[ \int_a^x f(t) d t = F(x) - F(a) \]

であり、\(x=b\)とおくと

\[ \int_a^b f(t) d t=F(b)-F(a) \]

すなわち、「定積分の値は、原始関数の積分上限での値\(F(b)\)から、下限での値\(F(a)\)を引いたもの」となる。

定積分を表す記号として

\[ [F(t)]_a^b=F(b)-F(a) \]

や

\[ \int_a^b f(t) d t=[F(t)]_a^b \]

や

\[ \int_a^b f(t) d t=\left.F(t)\right|_a ^b \]

という記号が用いられる

定積分の計算

\[ \left. \int_a^b f(x) d x = F(x) \right|_a^b =F(b)-F(a) \]

広義積分#

区間内で不連続点がある場合や、無限区間での積分へ拡張した定積分を 広義積分（improper integral）という。

2種類ある

  1. 被積分関数 \(f(x)\) が区間 \(a \leqq x \leqq b\) で有限個の不連続点を持つ.

  2. 積分の上限, 下限の一方または両方が無限大である.

不連続な被積分関数#

関数 \(f(x)\) が区間 \(a < x \leqq b\) で連続であるとき、もし極限

\[ \lim_{\varepsilon \rightarrow+0} \int_{a+\varepsilon}^b f(x) d x \]

が存在するならば、 \(f(x)\) は \(a \leqq x \leqq b\) で積分可能であるといい、この極限値を

\[ \int_a^b f(x) d x \]

で表わす。同様に、 \(f(x)\) が \(a \leqq x<b\) で連続であるとき（下の式の右辺が存在するならば）、

\[ \int_a^b f(x) d x=\lim _{\varepsilon \rightarrow+0} \int_a^{b-\varepsilon} f(x) d x \]

と表わす。

いま \(f(x)\) が \(a \leqq x \leqq b\) 内の 1 点 \(c\) を除いて連続であるならば（下の式の右辺 の 2 つの極限が存在すると仮定して）

\[ \int_a^b f(x) d x=\lim _{\varepsilon_1 \rightarrow+0} \int_a^{c-\varepsilon_1} f(x) d x+\lim _{\varepsilon_2 \rightarrow+0} \int_{c+\varepsilon_2}^b f(x) d x \]

区間\(a\leq x \leq b\) 内に有限個の不連続点が存在するならば、この区間をいくつかの部分区間に分けて、そのいずれにもただ 1 つの不連続点があるようにできるので、同様に扱うことができる。

上記のような極限が存在するとき、 広義積分は収束する という。

無限区間の積分#

関数\(f(x)\)が\(x\geq a\)で連続であって、極限

\[ \lim _{b \rightarrow+\infty} \int_a^b f(x) d x \]

が存在するならば、この極限値を

\[ \int_a^{\infty} f(x) d x \]

で表わす。同様にして、

\[\begin{split} \begin{aligned} & \int_{-\infty}^b f(x) d x=\lim _{a \rightarrow-\infty} \int_a^b f(x) d x \\ & \int_{-\infty}^{\infty} f(x) d x=\lim _{a \rightarrow-\infty} \lim _{b \rightarrow \infty} \int_a^b f(x) d x \end{aligned} \end{split}\]

が定義される。

Contents