離散確率分布

離散確率分布#

離散確率分布（discrete probability distribution） は、0でない確率をとる確率変数値が高々可算個の確率分布のこと。

離散一様分布#

離散型確率変数\(X\)が

\[ P(X=x|N) = \frac{1}{N}, x=1,2,...,N \]

なる確率関数をもつとき、\(X\)は離散一様分布（discrete uniform distribution）に従うという。

\[ E[X] = \frac{1}{N} \sum^N_{x=1} x = \frac{N + 1}{2} \]
\[ V[X] = \frac{(N + 1)(N-1)}{12} \]

ベルヌーイ分布#

ベルヌーイ試行とは、\(p\)の確率で「成功」、\(1-p\)の確率で「失敗」する実験を行うことをいう。

確率変数\(X\)が成功のとき1、失敗のとき0をとるものとすると、確率関数は

\[\begin{split} P(X=x|p) = \begin{cases} p & (x=1)\\ 1-p & (x=0) \end{cases} \end{split}\]

と書ける。これをベルヌーイ分布（Bernoulli distribution）という。

\[\begin{split} \begin{align} E[X] &= 1 \times p + 0 \times (1 - p) = p\\ V[X] &= (1-p)^2 \times p + (0-p)^2 \times (1 - p) = p(1-p) \end{align} \end{split}\]

二項分布#

ベルヌーイ試行を独立に\(n\)回行ったときの「成功」の回数の分布

\(i=1,2,...,n\)に対して確率変数\(X_i\)を成功のとき1、失敗のとき0をとるものとすると、「成功」の回数は\(Y=\sum^n_{i=1}X_i\)と表すことができる。

\(Y=k\)となる確率は以下のようになる。

\[ P(Y=k) = {}_n C_k p^k (1 - p)^{n-k} \]

例：\(Y=2\)となる確率の場合

成功が2回、失敗が\(n-2\)回とする。

「成功」の事象を\(A_i\)、「失敗」の事象を\(A_i^c\)とすると、最初の2回が「成功」となる事象の確率は

\[ P(A_1 \cap A_2 \cap A_3^c \cap \cdots \cap A_n^c) \]

と表すことができる。

試行の独立性と\(P(A_i)=p, P(A_i^c)=1-p\)から

\[\begin{split} \begin{align} &P(A_1 \cap A_2 \cap A_3^c \cap \cdots \cap A_n^c)\\ &= P(A_1)P(A_2)P(A_3^c)\times\cdots\times P(A_n^c)\\ &= p^2(1-p)^{n-2} \end{align} \end{split}\]

と書くことができる。

\(n\)回試行して2回成功する事象の組み合わせは\(A_1 \cap A_2^c \cap A_3 \cap \cdots \cap A_n^c\)や\(A_1^c \cap A_2^c \cap A_3 \cap \cdots \cap A_n\)など他にも考えられ、その場合の数は組み合わせの数になるため\({}_n C_2\)となる。

したがって、\(Y=2\)となる確率は

\[ P(Y=2) = {}_n C_2 p^2 (1 - p)^{n-2} \]

となり、この\(2\)を\(k\)にすれば上記のものになる

\[\begin{split} E[X] = np\\ V[X] = np(1-p) \end{split}\]
Hide code cell source 
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
import pandas as pd

from scipy.stats import binom

np.random.seed(0)
n = 10
p = 0.5
k = range(0, 10)
pmf = binom.pmf(k, n=n, p=p)

fig, ax = plt.subplots()
ax.bar(k, pmf)
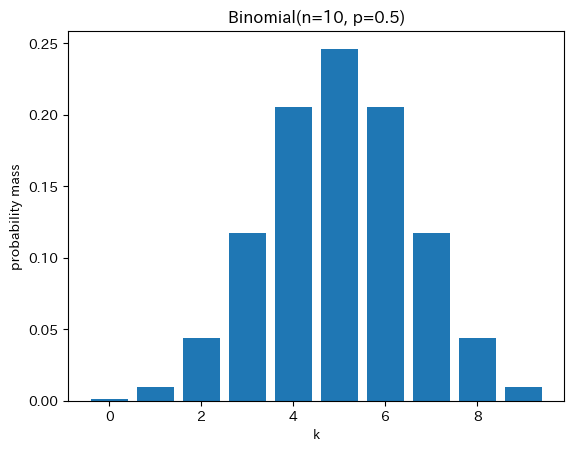
ax.set(title=f"Binomial(n={n}, p={p})", xlabel="k", ylabel="probability mass")
fig.show()
../../_images/f21b4526a7b547fce286da7a628a893a9ab3398a246b58c9200fef725915ced6.png