指数関数と対数関数

指数関数

（定義）指数関数

\(a\)をある定数として、

\[ y = a^x \]

を、\(a\)を 底 とする 指数関数（exponential function）という。

ネイピア数

以下で定義される定数\(e\)をネイピア数という

\[ \lim _{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^n=e=2.7182818 \cdots \]

（定義）自然指数関数

\(e\)を底とする指数関数

\[ y = e^x \]

を 指数関数（the exponential function）あるいは明示的に 自然指数関数という。

（英語だとtheがつくかどうかで底の違いを表現する。日本語だとややこしいが、標準的な指数関数は\(e\)を底とする指数関数である）

Show code cell source

Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-2, 2, 100)
y = np.array([np.exp(xi) for xi in x])

fig, ax = plt.subplots(figsize=[4, 2])
ax.plot(x, y, label=r"$\exp(x)$")
ax.set(xlabel="x", ylabel="y")
ax.axhline(color="gray")
ax.axvline(color="gray")
ax.legend()
fig.show()

\(x=0\)のとき、\(e^0 = 1\)

\(x=1\)のとき、\(e^1 = e\)

\(x=-1\)のとき、\(e^{-1} = \frac{1}{e} = 0.3678 \cdots\)

（定義）自然指数関数

指数関数にはいくつかの定義があり、オイラーによって最初に定義されたものは以下のものになる

\[ \exp (x)=\lim _{n \rightarrow \infty}\left(1+\frac{x}{n}\right)^n \]

マクローリン級数によって冪級数の形にした

\[ \exp (x)=\sum_{n=0}^{\infty} \frac{x^n}{n !}=1+x+\frac{x^2}{2 !}+\frac{x^3}{3 !}+\frac{x^4}{4 !}+\cdots \]

の定義もある

\(\left(1+\frac{x}{n}\right)^n\)を有限の範囲でいくつか試すと以下のようになる

x = 1
for n in range(1, 6):
    e = (1 + (x / n))**n
    print(f"{n=}, {e=:.3f}")

n=1, e=2.000
n=2, e=2.250
n=3, e=2.370
n=4, e=2.441
n=5, e=2.488

Show code cell source

Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

N = np.linspace(1, 100, 101)
E = [(1 + (x / n))**n for n in N]

fig, ax = plt.subplots(figsize=[4, 2])
ax.plot(N, E)
ax.set(
    xlabel="n",
    ylabel=r"$(1 + \frac{x}{n})^n$",
    title=r"$(1 + \frac{x}{n})^n, x=1$",
    yticks=[2, np.exp(1),3],
)
ax.axhline(np.exp(1), color="gray")
ax.axvline(color="gray")
fig.show()

指数(関数)の基本的性質（指数法則）

指数法則

\[\begin{split} \begin{align} a^x a^y &= a^{x+y} \\ \left(a^x\right)^y &= a^{x y} \\ \frac{a^x}{a^y} &= a^{x-y} \\ \left(\frac{a}{b}\right)^x &= \frac{a^x}{b^x} \end{align} \end{split}\]

例：\(x^{-1}\) は？

\(x^{-1}\)と\(x\)を乗じれば\(x^{-1} \times x^1 = x^{-1 + 1} = x^0 = 1\)となる。

なので\(x^{-1} = \frac{1}{x}\)となる。一般に\(x^{-n}\)も同様。

例：\(x^{\frac{1}{2}}\) は？

\(x^{\frac{1}{2}}\)と\(x^{\frac{1}{2}}\)を乗じれば\(x^{\frac{1}{2}} \times x^{\frac{1}{2}} = x^{\frac{1}{2} + \frac{1}{2}} = x\)となる。

なので\(x^{\frac{1}{2}} = \sqrt{x}\)

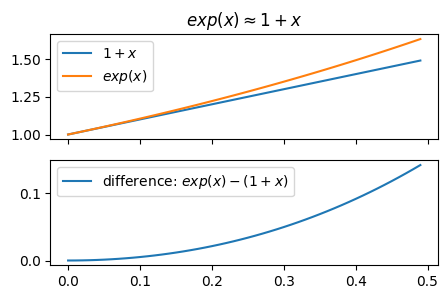
\(x\)を0.01増やすと\(y\)が1%増える

\(x\)を0.01増やすと\(y\)が1%増える

自然指数関数

\[ y = \exp(x) = e^x \]

は、\(x\)を0.01増やすと\(y\)が1%増えるように底が調整されている（底がネイピア数\(e\)だとそのようになる）

この誤差は\(x\)が大きくなるにつれて大きくなる

Show code cell source

Hide code cell source

import numpy as np
import pandas as pd

x = np.linspace(0, 0.1, 11)
y = np.exp(x)

display(pd.DataFrame(dict(x=x, y=y)).round(3))

	x	y
0	0.00	1.000
1	0.01	1.010
2	0.02	1.020
3	0.03	1.030
4	0.04	1.041
5	0.05	1.051
6	0.06	1.062
7	0.07	1.073
8	0.08	1.083
9	0.09	1.094
10	0.10	1.105

Show code cell source

Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(0, 0.5, 0.01)
y = np.exp(x)

fig, axes = plt.subplots(nrows=2)
axes[0].plot(x, 1+x, label=r"$1 + x$")
axes[0].plot(x, y, label=r"$exp(x)$")
axes[0].legend()
axes[1].plot(x, y - (1+x), label=r"difference: $exp(x) - (1 + x)$")
axes[1].legend()
axes[0].set(title=r"$exp(x) \approx 1 + x$")
fig.show()

対数関数

指数関数の逆関数を 対数関数 （logarithmic function）という。

\(a^y = x\)のとき、「\(y\)は\(a\)を 底 とする \(x\) の対数」といい

\[ y = \log_{a} x \]

と表す。

（定義）対数

\(a > 0, a \neq 1, M > 0\)について

\[ a^m = M \Longleftrightarrow m = \log_a M \]

Show code cell source

Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0.1, 5, 100)
y = np.array([np.log(xi) for xi in x])

fig, ax = plt.subplots(figsize=[4, 2])
ax.axhline(color="gray")
ax.axvline(color="gray")
ax.plot(x, y, label=r"$\log(x)$")
ax.set(xlabel="x", ylabel="y")
ax.legend()
fig.show()

対数関数の性質

\(a > 0, a \neq 1, b > 0, M > 0, N > 0\)に対して

\[\begin{split} \begin{align} \log_a 1 &= 0\\ \log_a a &= 1\\ \log_a \frac{x}{y} &= \log_a x - \log_a y\\ \log_a xy &= \log_a x + \log_a y\\ \log_a x^y &= y \log_a x\\ \log_b x &= \frac{\log_a x}{\log_a b}\\ \end{align} \end{split}\]

例：\(a^x\)

底が\(a\)の対数を取る場合

\[ \log_a (a^x) = x \]

自然対数を使う場合

\[ \ln (a^x) = x \ln(a) \quad (\because \log x^y = y \log x の性質より) \]

元本が2倍になる年数は

例：元本が2倍になる年数は？

年率5%の利益が複利で運用できるとして、元本が2倍になるには何年かかる？

利率\(r\)で\(n\)年間複利運用したときの利益率\(\pi\)は

\[ (1 + r)^n = \pi \]

\(r=0.05\)とすると、\(\pi=2\)になるのは

\[ (1.05)^n = 2 \]

両辺の対数をとると

\[\begin{split} \log_{10} (1.05)^n = \log_{10} 2 \\ \to n \log_{10} 1.05 = \log_{10} 2 \\ \to n = \frac{ \log_{10} 2 }{ \log_{10} 1.05 } \approx 14.2 \end{split}\]

なので約14年かかることになる。

import numpy as np
np.log10(2) / np.log10(1.05)

14.206699082890461

\(\ln(1.01) \approx 0.01\)

\(x\)を1%増やすと\(y = \ln(x)\)は0.01増える： \(\ln( 1 + 0.01) \approx 0.01\)

\(\ln(1.01) \approx 0.01\)はテイラー近似から導出される。まずテイラー近似について述べる

\(f(x)=\ln(x+1)\)とおくと、その\(n\)次の微分は

\[ f^{(n)}(x) = (-1)^{n-1} \frac{(n-1)!}{(x+1)^n} \]

となる。もし\(x=0\)なら

\[ f^{(n)}(0) = (-1)^{n-1} \frac{(n-1)!}{(1)^n} = (-1)^{n-1} (n-1)! \]

となる。

これを\(x=0\)でのテイラー展開（つまりマクローリン展開）

\[ \sum^{\infty}_{n=0} \frac{f^{(n)}(0)}{n!}x^n = f(0) + f'(0) x + \frac{f^{(2)}(0)}{2!}x^2 + \cdots \]

にあてはめると、

\[ \ln(1 + x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots \]

となる。これは\(x\)が極めて小さな値（\(x \approx 0\)）であれば\(x^2\)や\(x^3\)といった値は非常に小さくなるため、\(\ln(1+x) \approx x\)となる。

よって\(\ln( 1 + 0.01) \approx 0.01\)となる

数値計算的に確かめると、以下のようになる

log: 0.0099503
approx 1: 0.0100000
approx 2: 0.0099500
approx 3: 0.0099503