区間推定#
区間推定（interval estimation）は推定したいパラメータ\(\theta\)の真の値がある区間\((L, U)\)に入る確率が\(1-\alpha\)以上（\(\alpha\)は\(\theta\)が区間に入らない確率）になる区間を推定する。つまり、
の\(L, U\)を推定する。
なお、この\(1-\alpha\)を信頼係数（confidence coefficient）といい、区間\([L, U]\)を信頼区間（confidence interval）と呼ぶ。
正規母集団の母平均の区間推定#
確率変数\(X\)の標本平均\(\bar{X}\)は中心極限定理により正規分布\(N(\mu, \sigma^2 / n)\)に従う。
これを標準化して
とすると、これは平均0、標準偏差1の標準正規分布に従う。
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy.stats import norm
z = np.linspace(-4, 4, 100)
y = norm.pdf(z)
fig, ax = plt.subplots(dpi=100, figsize=[6, 3])
ax.set(title="標準正規分布", xlabel="Z", xlim=(-4, 4))
ax.plot(z, y, color="dimgray")
ax.axhline(y=0, color="dimgray", linewidth=1)
alpha = 0.05 / 2
for a in [alpha, (1 - alpha)]:
x = norm.ppf(a)
ax.axvline(x=x, color="steelblue")
if x < 0:
ax.text(x - 0.1, norm.pdf(x) + 0.01, f"Z = {x:.2f}", color="steelblue", horizontalalignment="right")
ax.fill_between(z, 0, y, where = z <= x, color="steelblue")
else:
ax.text(x + 0.1, norm.pdf(x) + 0.01, f"Z = {x:.2f}", color="steelblue", horizontalalignment="left")
ax.fill_between(z, 0, y, where = z >= x, color="steelblue")
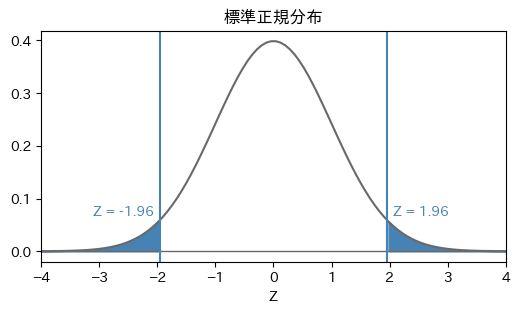
標準正規分布は\((-\infty, \infty)\)の範囲にわたって確率密度関数がゼロでない領域が存在するが、図のように正規分布の両端でそれぞれ確率\(\alpha/2\)分だけ推定を誤る可能性を許容すると、一定の範囲で区切ることができる。図は\(\alpha=0.05\)として、両側それぞれでその半分の確率\(\alpha / 2 = 0.025\)の領域で区切っており、それに相当する\(Z\)の値が\(Z \pm 1.96\)である。
一般化してこのような値を\(Z_{\alpha/2}\)と表すことにすると、区間推定は
となり、これを\(\mu\)について解くと
であり、信頼区間は
となる。
pythonでの実装#
母集団が\([0, 1]\)の範囲の値をとる一様分布\(U(0, 1)\)（母平均\(\mu=\frac{0+1}{2} = 0.5\)）であるとし、そこから得た次のようなサンプルがあるとする。
Show code cell source
np.random.seed(0)
n = 100
x = np.random.uniform(low=0, high=1, size=n)
mu = 0.5 # 母平均
fig, ax = plt.subplots()
ax.hist(x)
ax.set(title="Histogram of Data")
ax.axvline(x.mean(), color="darkorange")
ax.text(x.mean() + 0.02, 1, f"標本平均: {x.mean():.3f}", color="darkorange", size=14)
ax.axvline(mu, color="limegreen")
ax.text(mu + 0.02, 3, f"母平均: {mu:.3f}", color="limegreen", size=14)
fig.show()
式をpythonに落とし込んで計算すると次のようになる
# ※ddof=1: 不偏標準偏差にするためのオプション
std_error = x.std(ddof=1) / np.sqrt(n)
# 信頼区間
alpha = 0.05
z = norm.ppf(1 - alpha / 2)
[x.mean() - z * std_error, x.mean() + z * std_error]
[0.4160030960878336, 0.5295845829372018]
statsmodelsのemplike.DescStatで計算することもできる
# statsmodelsを使う場合
from scipy.stats import norm
import statsmodels.api as sm
el = sm.emplike.DescStat(x)
el.ci_mean()
(0.4166429503391242, 0.5294769896986984)
scipy.stats の norm.interval() で計算することもできる。
from scipy.stats import norm, sem
norm.interval(confidence=0.95, loc=x.mean(), scale=sem(x))
# ※ sem は standard error of mean、つまり x.std(ddof=1) / np.sqrt(n)と等しい
(0.4160030960878336, 0.5295845829372018)
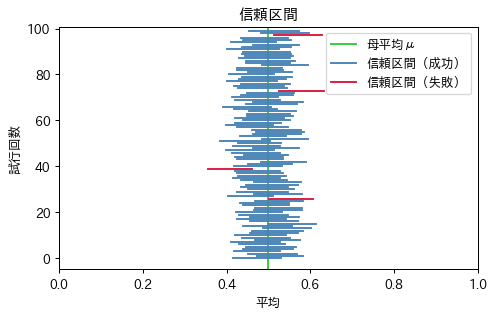
サンプルをとって95%信頼区間を計算する作業を100回繰り返したものが以下の図である。\(\alpha=0.05\)なので、100回の調査で5回程度は推定を誤る（信頼区間に母平均が含まれない）可能性がある。
Show code cell source
np.random.seed(0)
fig, ax = plt.subplots(dpi=90, figsize=[6, 3.5])
ax.set(title="信頼区間", xlabel="平均", ylabel="試行回数")
ax.axvline(mu, color="limegreen", label="母平均μ")
is_first_success = True
is_first_fail = True
n_trial = 100
for i in range(n_trial):
x = np.random.uniform(size=n)
lower, upper = norm.interval(confidence=0.95, loc=x.mean(), scale=sem(x))
args = dict(y=i, xmin=lower, xmax=upper)
if mu < lower or upper < mu:
# 凡例表示のため初回だけlabelをつける
if is_first_fail:
ax.axhline(**args, color="crimson", label="信頼区間（失敗）")
is_first_fail = False
else:
ax.axhline(**args, color="crimson")
else:
if is_first_success:
ax.axhline(**args, color="steelblue", label="信頼区間（成功）")
is_first_success = False
else:
ax.axhline(**args, color="steelblue")
ax.legend()
fig.show()
\(t\)検定#
母分散が未知の場合、\(t\)分布を用いる。標本標準偏差を\(s\)とすると、
は自由度\(n-1\)の\(t\)分布に従うため、
となる。