ベクトル#
シンプルな定義#
数を並べた組をベクトルという。
\[
% 太字のalias
\newcommand{\b}[1]{\boldsymbol{#1}}
%
\boldsymbol{a} = (a_1, a_2, a_3)
\]
もっと厳密な定義#
任意の元\(x, y \in L\)と任意の実数\(a, b\)について実数倍\(ax, by\)とそれらの和\(ax + by\)が定義されており、 かならず\(ax + by \in L\)が成り立つような集合\(L\)を ベクトル空間（vector space） という。また\(L\)の元を ベクトル（vector） という
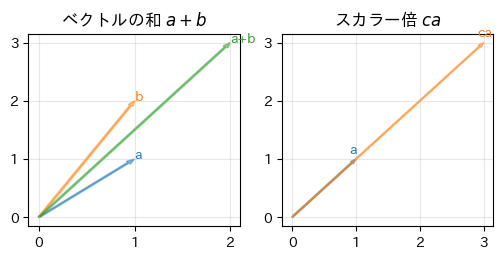
ベクトルの和とスカラー倍#
2つの\(n\)次元ベクトル
\[\begin{split}
\b{a} =
\begin{pmatrix}
a_1\\
\vdots\\
a_n
\end{pmatrix}
, \hspace{2em}
\b{b} =
\begin{pmatrix}
b_1\\
\vdots\\
b_n
\end{pmatrix}
\end{split}\]
とスカラー\(c\)があるとする。
足し算#
ベクトル\(\b{a},\b{b}\)の足し算を次のように定義する
\[\begin{split}
\b{a}+\b{b} =
\begin{pmatrix}
a_1\\
\vdots\\
a_n
\end{pmatrix}
+
\begin{pmatrix}
b_1\\
\vdots\\
b_n
\end{pmatrix}
=
\begin{pmatrix}
a_1 + b_1\\
\vdots\\
a_n + b_n
\end{pmatrix}
\end{split}\]
スカラー倍#
ベクトル\(\b{a}\)のスカラー\(c\)倍を次のように定義する
\[\begin{split}
c \b{a} =
\begin{pmatrix}
c a_1\\
\vdots\\
c a_n
\end{pmatrix}
\end{split}\]
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import japanize_matplotlib
a = np.array([1, 1])
b = np.array([1, 2])
o = np.array([0, 0])
c = 3
fig, axes = plt.subplots(ncols=2, figsize=[6, 2.5])
# 和
ax = axes[0]
cmap = mpl.colormaps['tab10']
for i, (v, label) in enumerate([(a, "a"), (b, "b"), ((a+b), "a+b")]):
ax.arrow(*o, *v, width=0.02, color=cmap(i), length_includes_head=True, alpha=0.5)
ax.text(v[0], v[1], label, color=cmap(i))
longest_v = (a+b)
ax.set(xticks=range(longest_v[0]+1), yticks=range(longest_v[1]+1), title=r"ベクトルの和 $a+b$")
ax.grid(True, alpha=0.3)
# スカラー倍
ax = axes[1]
for i, (v, label) in enumerate([(a, "a"), (a * c, "ca")]):
ax.arrow(*o, *v, width=0.02, color=cmap(i), length_includes_head=True, alpha=0.5)
ax.text(v[0] - 0.1, v[1] + 0.1, label, color=cmap(i))
longest_v = c * a
ax.set(xticks=range(longest_v[0]+1), yticks=range(longest_v[1]+1), title=r"スカラー倍 $c a$")
ax.grid(True, alpha=0.3)
fig.show()
