決定木

Contents

決定木#

回帰木#

\(M\)次元の特徴量\(\boldsymbol{x}\in \mathbb{R}^M\)と教師ラベル\(y\)のペアからなるサンプルが\(N\)個あるとする。

回帰木（regression tree）は特徴空間を\(K\)個の領域に区切ったもの

\[ \hat{y}_i = \sum^K_{k=1} f_k(x) \]

ここで\(f_k(x) = w_{q(x)}\)で、$q: \mathbb{R}^M \to R

import numpy as np
import matplotlib.pyplot as plt

n = 10
np.random.seed(0)

# class 0
y0 = np.zeros(shape=(n//2, ))
x0 = np.random.normal(loc=(-1, -1), scale=0.8, size=(n//2, 2))

# class 1
y1 = np.ones(shape=(n//2, ))
x1 = np.random.normal(loc=(1, 1), scale=0.8, size=(n//2, 2))

y = np.append(y0, y1)
X = np.append(x0, x1, axis=0)

fig, ax = plt.subplots()
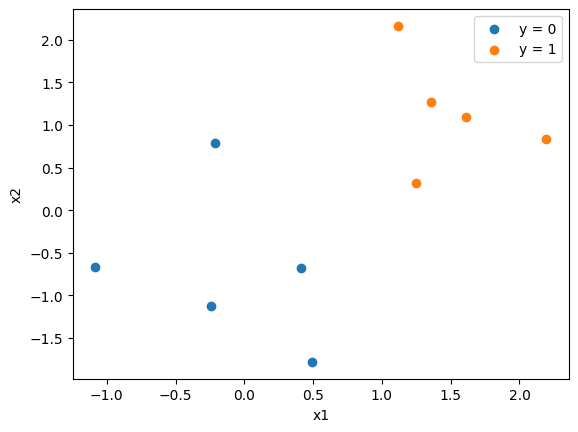
ax.scatter(X[(y == 0), 0], X[(y == 0), 1], label="y = 0")
ax.scatter(X[(y == 1), 0], X[(y == 1), 1], label="y = 1")
ax.legend()
ax.set(xlabel="x1", ylabel="x2")
fig.show()
../../_images/6956dff87e79e3ee82ce57068e38a0500d48607d6dc75b11b63aa59186a653d3.png 
for x in X[:, 0]:
    x
Contents