内積

\(k\)次元のベクトル\(\boldsymbol{a} = (a_1, a_2, \dots, a_k)^T, \ \boldsymbol{b} = (b_1, b_2, \dots, b_k)^T\)があるとき、

\[ \sum^k_{i=1} a_i b_i \]

という演算を内積（inner product）といい、\(\boldsymbol{a}^T \boldsymbol{b}\)や\(\boldsymbol{a} \cdot \boldsymbol{b}\)や\((\boldsymbol{a}, \boldsymbol{b})\)や\(\langle\boldsymbol{a}, \boldsymbol{b} \rangle\)と表す

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import japanize_matplotlib

a = np.array([1, 1, 1])
b = np.array([2, 2, 2])
a.T @ b

6

内積と類似度

Note

コサイン類似度 2つのベクトル\(\boldsymbol{a} = (a_1, a_2, \dots, a_k)^T\)と\(\boldsymbol{b} = (b_1, b_2, \dots, b_k)^T\)について、

\[ \cos(\boldsymbol{a}, \boldsymbol{b}) = \frac{ \boldsymbol{a}^T \boldsymbol{b} }{ ||\boldsymbol{a}|| \ ||\boldsymbol{b}|| } = \frac{ \sum^k_{i=1} a_i b_i } { \sqrt{ \sum^k_{i=1} a_i^2 } \sqrt{ \sum^k_{i=1} b_i^2 } } \]

をコサイン類似度という

\[\begin{split} \newcommand{\b}[1]{\boldsymbol{#1}} \boldsymbol{a}^T \boldsymbol{b} = ||\boldsymbol{a}|| \ ||\boldsymbol{b}|| \cos(\boldsymbol{a}, \boldsymbol{b}) \\ \implies \cos(\boldsymbol{a}, \boldsymbol{b}) = \frac{ \boldsymbol{a}^T \boldsymbol{b} }{ ||\boldsymbol{a}|| \ ||\boldsymbol{b}|| } \end{split}\]

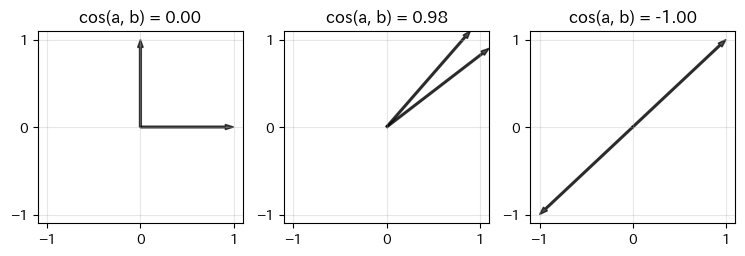
コサイン類似度はベクトルを矢印で表現したときに同じ方向を向いているほど1に近く、真逆の方向ほど-1に近くなる

def cos(a, b):
    return (a.T @ b) / (np.linalg.norm(a) * np.linalg.norm(b))

cos(a, b)

1.0000000000000002

Show code cell source Hide code cell source

o = np.array([0, 0])
buffer = 0.1
lim = np.array([-1, 1]) * (1 + buffer)
ticks = [-1, 0, 1]

datasets = [
    [np.array([1, 0]), np.array([0, 1])],
    [np.array([1.1, 0.9]), np.array([0.9, 1.1])],
    [np.array([1, 1]), np.array([-1, -1])],
]
m = len(datasets)
fig, axes = plt.subplots(ncols=m, figsize=[m*3, 2.5])
for i in range(m):
    a, b = datasets[i]
    axes[i].arrow(*o, *a, width=0.02, color="black", length_includes_head=True, alpha=0.7)
    axes[i].arrow(*o, *b, width=0.02, color="black", length_includes_head=True, alpha=0.7)
    axes[i].grid(True, alpha=0.3)
    axes[i].set(title=f"cos(a, b) = {cos(a, b):.2f}", xticks=ticks, yticks=ticks, xlim=lim, ylim=lim)

fig.show()

直交

直交

ベクトル\(\boldsymbol{a}, \boldsymbol{b} \in \mathbb{R}^n\)が

\[ \boldsymbol{a}^T \boldsymbol{b} = 0 \]

を満たすとき、\(\boldsymbol{a} \boldsymbol{b}\)は直交しているという