極値

極大と極小

ある関数\(y=f(x)\)があるとする。

ある点\(a\)での値\(f(a)\)がその近くでのほかの値\(f(a+h), (h\neq 0)\)より大きい場合、\(f(x)\)は\(a\)で 極大 （maximum）になるといい、\(f(a)\)を 極大値 という。

ある点\(a\)での値\(f(a)\)がその近くでのほかの値\(f(a+h), (h\neq 0)\)より小さい場合、\(f(x)\)は\(a\)で 極小 （minimum）になるといい、\(f(a)\)を 極小値 という。

極大値と極小値を総称して 極値 という。

極値の判定

極値の条件

極値の条件

関数 \(y=f(x)\) が \(c \leqq x \leqq e\) で微分可能であり、 点 \(x_0(c<x_0<e)\) で極大值または 極小値をとるならば、 \(f^{\prime}(x_0)=0\) である。

証明

点\(x=x_0\)で\(f(x)\)が極大値を取るとする。極値の定義から、\(f(x_0 + h) < f(x_0)\)、すなわち

\[ f\left(x_0+h\right)-f\left(x_0\right)<0 \quad(h \neq 0) \]

\(h>0\) ならぱ

\[ \frac{f\left(x_0+h\right)-f\left(x_0\right)}{h}<0, \quad f^{\prime}\left(x_0+0\right)=\lim _{h \rightarrow+0} \frac{f\left(x_0+h\right)-f\left(x_0\right)}{h} \leqq 0 \]

\(h<0\) ならば

\[ \frac{f\left(x_0+h\right)-f\left(x_0\right)}{h}>0, \quad f^{\prime}\left(x_0-0\right)=\lim _{h \rightarrow-0} \frac{f\left(x_0+h\right)-f\left(x_0\right)}{h} \geqq 0 \]

よって

\[ f^{\prime}\left(x_0+0\right)=f^{\prime}\left(x_0-0\right)=f^{\prime}\left(x_0\right) \]

なので \(0 \leqq f^{\prime}\left(x_0\right) \leqq 0\) より、 \(f^{\prime}\left(x_0\right)=0\)

極値の判定法

導関数のふるまいで極値を判定できる。まとめると次のようになる。

\(x\) が増加しながら \(x_0\) を通過するとき

1. 導関数 \(f^{\prime}(x)\) が正から 0 を通って負に符号をかえるならば、\(f(x)\) は \(x=x_0\) で極大值 \(f\left(x_0\right)\) をもつ。

2. 導関数 \(f^{\prime}(x)\) が負から 0 を通って正に符号をかえるならば、\(f(x)\) は \(x=x_0\) で極小值 \(f\left(x_0\right)\) をもつ。

3. 導関数 \(f^{\prime}(x)\) が符号をかえないならば、 \(f^{\prime}\left(x_0\right)=0\) であっても、\(f(x)\) は \(x=x_0\) で極大にも極小にもならない

\(f'(x)\)の符号の判定に2次導関数\(f''(x)\)を使うことができる。

\(f'(x_0)=0\)のとき、\(f''(x_0) < 0\)であることは\(f'(x)\)が減少状態であり、\(x=x_0\)において正から0を通って負になることがわかる。

\(f'(x_0)=0\)のとき、\(f''(x_0) > 0\)であることは\(f'(x)\)が増加状態であり、\(x=x_0\)において負から0を通って正になることがわかる。

Show code cell source

Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

def f(x):
    return np.sin(x)

def f1(x):
    return np.cos(x)

def f2(x):
    return -np.sin(x)


x = np.linspace(0, 6, 100)

fig, ax = plt.subplots(figsize=[7, 3])

ax.plot(x, f(x), label=r"$f(x)$", color="steelblue")
ax.plot(x, f1(x), label=r"$f'(x)$", color="dodgerblue", linestyle="--", alpha=0.6)
ax.plot(x, f2(x), label=r"$f''(x)$", color="deepskyblue", linestyle="-.", alpha=0.6)

x0 = np.pi/2
x1 = 3*np.pi/2
ax.axvline(x=x0, color="gray", alpha=0.5, linestyle=":")
ax.axvline(x=x1, color="gray", alpha=0.5, linestyle=":")
ax.axhline(y=0, color="gray", alpha=0.8)

ax.legend()
ax.set(xlabel="x", ylabel="y")
ax.text(x0, f(x0) - 0.15, "極大", color="steelblue", ha="center")
ax.text(x1, f(x1) + 0.15, "極小", color="steelblue", ha="center")
ax.text(x0, f1(x0) - 0.15, r"$f'(x)=0$", color="dodgerblue", ha="center")
ax.text(x1, f1(x1) - 0.15, r"$f'(x)=0$", color="dodgerblue", ha="center")
ax.text(x0, f2(x0) + 0.15, r"$f''(x)<0$", color="deepskyblue", ha="center")
ax.text(x1, f2(x1) - 0.2, r"$f''(x)>0$", color="deepskyblue", ha="center")
fig.show()

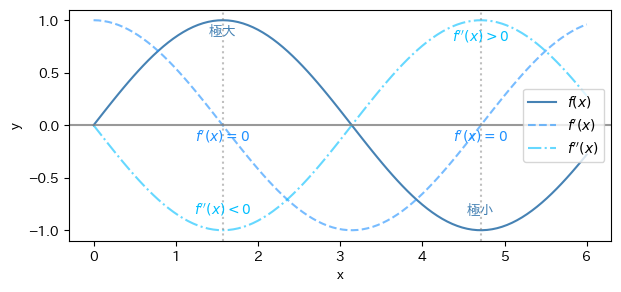
よって、きょくちのはんて

極値の判定法

(1) \(f^{\prime}\left(x_0\right)=0, f^{\prime \prime}\left(x_0\right)<0\) ならば、 関数 \(f(x)\) は \(x=x_0\) で極大值 \(f\left(x_0\right)\) をとる。

(2) \(f^{\prime}\left(x_0\right)=0, f^{\prime \prime}\left(x_0\right)>0\) ならば、 関数 \(f(x)\) は \(x=x_0\) で極小値 \(f\left(x_0\right)\) をとる。

最大値と最小値

閉区間\(a \leq x \leq b\)で連続な関数\(f(x)\)の最大値と最小値を考える。

この場合、次の2点に注意する必要がある。

1. 区間内に極大（または極小）になる点が複数あり得るため、それらを比べて最大値（最小値）を探索する必要がある

2. 区間の端点\(a, b\)が最大値（最小値）になる可能性があるため、端点とも比較する必要がある