概要

概要#

単回帰モデル#

モデル#

説明変数 $x$ と被説明変数 $y$ の $N$ 個のサンプルからなるデータセット ${(y_{i}, x_{i})}_{i = 1}^{N}$ があるとする。

これに対する次のようなモデルを単回帰モデルという。

y_{i} = β_{0} + β_{1} x_{i} + ε_{i}

パラメータの推定#

通常最小二乗法（ordinary least squares: OLS）という方法を使うのが最も一般的である。これは実測値 $y_{i}$ と予測値 ${\hat{y}}_{i} = β_{0} + β_{1} x_{i}$ との残差（residual） $y_{i} - {\hat{y}}_{i}$ の二乗和（residual sum of squares）

R S S = \sum_{i = 1}^{N} (y_{i} - {\hat{y}}_{i})^{2} = \sum_{i = 1}^{N} (y_{i} - β_{0} - β_{1} x_{i})^{2}

を最小化するようにパラメータを推定するというもの。

この最適化は、まずRSSをパラメータ $β_{0}, β_{1}$ について微分し、これがゼロとなるようなパラメータを求める。

\begin{array}{r} {\begin{aligned} \frac{\partial R S S}{\partial β_{0}} & = - 2 \sum_{i = 1}^{N} (y_{i} - β_{0} - β_{1} x_{i}) = 0 \\ \frac{\partial R S S}{\partial β_{1}} & = - 2 \sum_{i = 1}^{N} (y_{i} - β_{0} - β_{1} x_{i}) x_{i} = 0 \end{aligned} \end{array}

これを整理すると

\begin{array}{r} {\begin{aligned} N β_{0} + \sum_{i = 1}^{N} β_{1} x_{i} & = \sum_{i = 1}^{N} y_{i} \\ \sum_{i = 1}^{N} β_{0} x_{i} + \sum_{i = 1}^{N} β_{1} x_{i}^{2} & = \sum_{i = 1}^{N} y_{i} x_{i} \end{aligned} \end{array}

となる。

1行目の両辺に $\frac{1}{N} \sum_{i = 1}^{N} x_{i}$ を乗じた

\sum_{i = 1}^{N} β_{0} x_{i} + \frac{1}{N} β_{1} (\sum_{i = 1}^{N} x_{i})^{2} = \frac{1}{N} (\sum_{i = 1}^{N} y_{i}) (\sum_{i = 1}^{N} x_{i})

を2行目から差し引くと

\begin{aligned} \sum_{i = 1}^{N} β_{1} x_{i}^{2} - \frac{1}{N} β_{1} (\sum_{i = 1}^{N} x_{i})^{2} & = \sum_{i = 1}^{N} y_{i} x_{i} - \frac{1}{N} (\sum_{i = 1}^{N} y_{i}) (\sum_{i = 1}^{N} x_{i}) \end{aligned}

両辺に $\frac{1}{N}$ を乗じると

\begin{aligned} \frac{1}{N} \sum_{i = 1}^{N} β_{1} x_{i}^{2} - β_{1} (\frac{1}{N} \sum_{i = 1}^{N} x_{i})^{2} & = \frac{1}{N} \sum_{i = 1}^{N} y_{i} x_{i} - (\frac{1}{N} \sum_{i = 1}^{N} y_{i}) (\frac{1}{N} \sum_{i = 1}^{N} x_{i}) \end{aligned}

少し整理すると

\begin{aligned} β_{1} (\frac{1}{N} \sum_{i = 1}^{N} x_{i}^{2} - (\frac{1}{N} \sum_{i = 1}^{N} x_{i})^{2}) & = \frac{1}{N} \sum_{i = 1}^{N} y_{i} x_{i} - (\frac{1}{N} \sum_{i = 1}^{N} y_{i}) (\frac{1}{N} \sum_{i = 1}^{N} x_{i}) \end{aligned}

\begin{array}{r} \begin{aligned} β_{1} & = \frac{\frac{1}{N} \sum_{i = 1}^{N} y_{i} x_{i} - (\frac{1}{N} \sum_{i = 1}^{N} y_{i}) (\frac{1}{N} \sum_{i = 1}^{N} x_{i})}{\frac{1}{N} \sum_{i = 1}^{N} x_{i}^{2} - (\frac{1}{N} \sum_{i = 1}^{N} x_{i})^{2}} \\ = \frac{\frac{1}{N} \sum_{i = 1}^{N} y_{i} x_{i} - \bar{y} \bar{x}}{\frac{1}{N} \sum_{i = 1}^{N} x_{i}^{2} - {\bar{x}}^{2}} \\ = \frac{C o v [x, y]}{V a r [x]} \end{aligned} \end{array}

$β_{0}$ については、上記の連立方程式の1つ目の式

N β_{0} + \sum_{i = 1}^{N} β_{1} x_{i} = \sum_{i = 1}^{N} y_{i}

を $N$ で割ると

\begin{array}{r} \begin{aligned} β_{0} & = \frac{1}{N} \sum_{i = 1}^{N} y_{i} - \frac{1}{N} \sum_{i = 1}^{N} β_{1} x_{i} \\ = \bar{y} - β_{1} \bar{x} \end{aligned} \end{array}

Note

最尤推定量（単回帰モデル）

β_{0} = \bar{y} - β_{1} \bar{x}, β_{1} = \frac{C o v [x, y]}{V a r [x]}

残差二乗和（RSS）の等高線を描いてみると、OLS推定値が極小値となっていることがわかる。（OLS以外のExamplesは適当な値を入れた単なる例。最適解からズレていることがわかる。）

Show code cell source Hide code cell source

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# data -------------------------
np.random.seed(0)
n = 10
beta_0 = 5
beta_1 = 10
x = np.sort(np.random.uniform(size=n))
e = np.random.normal(scale=2, size=n)
y = beta_0 + beta_1 * x + e

# calc RSS ---------------------
def rss(y_true, x, beta_0, beta_1):
    y_pred = beta_0 + beta_1 * x
    return sum((y_true - y_pred)**2)

beta_0_range = np.linspace(-5, 20, 26)
beta_1_range = np.linspace(-5, 20, 26)
Beta0, Beta1 = np.meshgrid(beta_0_range, beta_1_range)
Loss = np.array([rss(y, x, b0, b1) for b0, b1 in zip(Beta0.flatten(), Beta1.flatten())]).reshape(Beta0.shape)

# OLS estimate ------------------
beta_1_hat = np.cov(x, y)[0, 1] / np.var(x)
beta_0_hat = y.mean() - beta_1_hat * x.mean()
loss_ = rss(y, x, beta_0_hat, beta_1_hat)
color_ols = "black"

# wrong estimate
beta_wrongs = [(15, -4), (5, 9)]
color_wrong = "red"

# plot ---------------------------
fig, axes = plt.subplots(ncols=2, figsize=[10,3])

# scatter
axes[0].scatter(x, y)
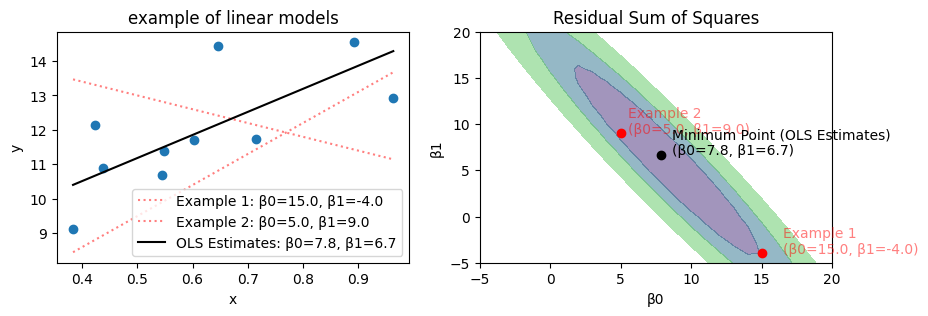
axes[0].set(xlabel="x", ylabel="y", title="example of linear models")

for i, (b0, b1) in enumerate(beta_wrongs, 1):
    y_pred = b0 + b1 * x
    axes[0].plot(x, y_pred, label=f"Example {i}: β0={b0:.1f}, β1={b1:.1f}", color=color_wrong, linestyle=":", alpha=.5)

y_pred = beta_0_hat + beta_1_hat * x
axes[0].plot(x, y_pred, label=f"OLS Estimates: β0={beta_0_hat:.1f}, β1={beta_1_hat:.1f}", color=color_ols)

axes[0].legend(loc="lower right")

# RSS
cs = axes[1].contourf(Beta0, Beta1, Loss, levels=[0, 50, 100, 200], alpha=0.5)
axes[1].set(xlabel="β0", ylabel="β1", title="Residual Sum of Squares")

for i, (b0, b1) in enumerate(beta_wrongs, 1):
    axes[1].scatter(b0, b1, color=color_wrong)
    axes[1].text(b0 * 1.1, b1, f"Example {i}\n(β0={b0:.1f}, β1={b1:.1f})", color=color_wrong, alpha=.5)

axes[1].scatter(beta_0_hat, beta_1_hat, color=color_ols)
axes[1].text(beta_0_hat * 1.1, beta_1_hat, f"Minimum Point (OLS Estimates)\n(β0={beta_0_hat:.1f}, β1={beta_1_hat:.1f})", color=color_ols)

fig.show()

# # 3d plot --------------------
# from matplotlib import cm
# fig, ax = plt.subplots(dpi=120, subplot_kw={"projection": "3d"})
# surf = ax.plot_surface(Beta0, Beta1, Loss, rstride=1, cstride=1, linewidth=1, antialiased=True, cmap=cm.coolwarm)
# fig.colorbar(surf, shrink=0.5, aspect=5, pad=0.11)
# ax.set(xlabel="beta_0", ylabel="beta_1", zlabel="Residual Sum of Squares")

# # # add a point
# # ax.scatter(beta_0_hat, beta_1_hat, loss_, color="darkorange")
# # ax.text(beta_0_hat * 0.99, beta_1_hat, loss_ * 1.1, f"Lowest point (β0={beta_0_hat:.1f}, β1={beta_1_hat:.1f})", color="darkorange")

# fig.show()

../../_images/b01a1fef248b8958c3df44d2c0fbe71156da67a9e3e05e9bf95fb97d137ac932.png

重回帰モデル#

説明変数を複数にしたものを重回帰モデルという。

モデル#

被説明変数を $N$ 次元ベクトル $y$ （ $N$ はサンプル数）、説明変数を $N \times (K + 1)$ 次元ベクトル $X$ （ $K$ は説明変数の次元数）、パラメータを $K + 1$ 次元ベクトル $β$ 、誤差項を $N$ 次元ベクトル $ε$ と書くと

\begin{array}{r} [\begin{array}{c} y_{1} \\ ⋮ \\ y_{N} \end{array}] = [\begin{array}{c} x_{10} & \dots & x_{1 K} \\ ⋮ & ⋮ \\ x_{N 0} & \dots & x_{N K} \end{array}] [\begin{array}{c} β_{0} \\ ⋮ \\ β_{K} \end{array}] + [\begin{array}{c} ε_{1} \\ ⋮ \\ ε_{N} \end{array}] \end{array}

を

y = X β + ε

と書くことができる

パラメータの推定#

残差二乗和を行列で表記すると

\begin{array}{r} \begin{aligned} R S S & = (y - X β)^{⊤} (y - X β) \\ = y^{⊤} y - y^{⊤} X β - β^{⊤} X^{⊤} y - β^{⊤} X^{⊤} X β \\ = y^{⊤} y - 2 y^{⊤} X β + β^{⊤} X^{⊤} X β \end{aligned} \end{array}

これを微分すると

\frac{\partial R S S}{\partial β} = - 2 X^{⊤} y + 2 (X^{⊤} X) β

となるため、これが0となるような $β$ は

β = (X^{⊤} X)^{- 1} X^{⊤} y

となる

概要

Contents

概要#

単回帰モデル#

モデル#

パラメータの推定#

重回帰モデル#

モデル#

パラメータの推定#