シミュレーション

Contents

シミュレーション#

import numpy as np

def m(X):
    return np.log(X)

def g(X):
    return X ** 2

def gen_data(n=500, seed=0, theta=5):
    np.random.seed(seed)
    V = np.random.normal(size=n, scale=2)
    U = np.random.normal(size=n, scale=3)
    X = np.random.uniform(size=n, low=1, high=10)
    D = m(X) + V
    Y = D * theta + g(X) + U
    X = X.reshape(-1, 1)
    return Y, D, X

Y, D, X = gen_data(seed=0)

import pandas as pd
import seaborn as sns
sns.pairplot(data=pd.DataFrame(dict(Y=Y, D=D, X=X.reshape(-1, ))))

<seaborn.axisgrid.PairGrid at 0x7f9430aee380>

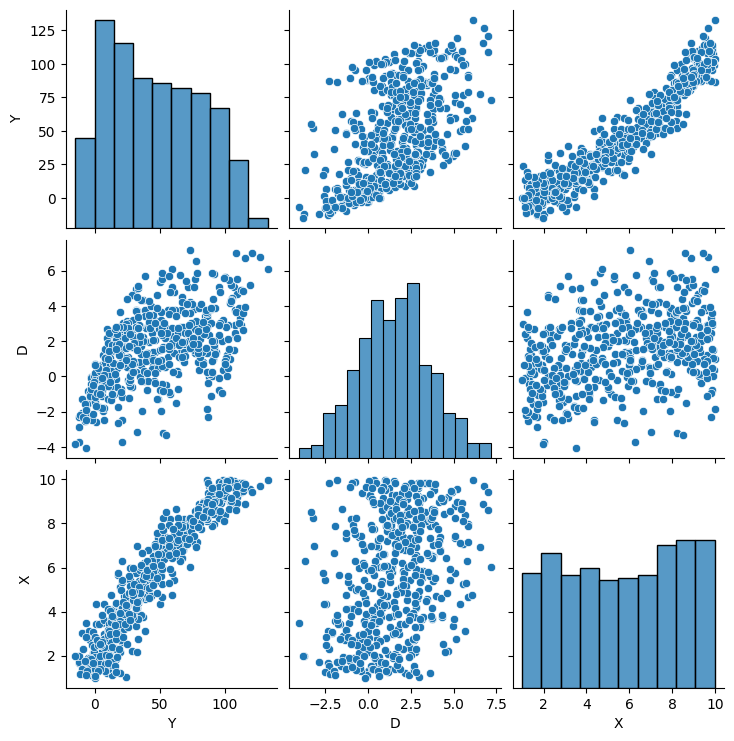
../../_images/da928cddcb901845d88f8c18bf79dd49ac45206c3728104bb3a700c4d2befe46.png

DML1を真似たやつ

サンプルを $K$ 個に分割する。
$k \in K$ について、 $k$ 番目のチャンクのサンプルのインデックスの集合を $I_{k}$ とする。 $i \notin I_{k}$ のサンプルで局外関数の推定を行う： ${\hat{η}}_{0, k} = ({\hat{η}}_{0} (W_{i})_{i \notin I_{k}})$
$i \in I_{k}$ のサンプルで $θ$ を推定
${\hat{θ}}_{0, k}$ の平均を集計

from lightgbm import LGBMRegressor
from sklearn.model_selection import KFold

def dml1(Y, D, X):
    kf = KFold(n_splits=5)
    kf.get_n_splits(X)
    thetas = []
    for i, (train_idx, test_idx) in enumerate(kf.split(X)):
        # 局外関数の推定
        m = LGBMRegressor(verbose=-1).fit(X[train_idx], D[train_idx])
        l = LGBMRegressor(verbose=-1).fit(X[train_idx], Y[train_idx])
        # 残差の計算
        V_hat = D[test_idx] - m.predict(X[test_idx])
        Y_res = Y[test_idx] - l.predict(X[test_idx])
        # θの推定
        theta_hat = np.mean(V_hat * V_hat) ** (-1) * np.mean(V_hat * Y_res)
        thetas.append(theta_hat)
    return np.mean(thetas)

dml1(Y, D, X)

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

4.996210951148309

DML#

%%time
theta = 5
n_rep = 1000
estimation_errors = []
for i_rep in range(n_rep):
    Y, D, X = gen_data(seed=i_rep, theta=theta)
    theta_hat = dml1(Y, D, X)
    estimation_error = theta - theta_hat
    estimation_errors.append(estimation_error)

import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.hist(estimation_errors, bins=30)
ax.set(xlabel=r"$\theta - \hat{\theta}$", title="Estimation Error")

mean_error = np.mean(estimation_errors)
ax.axvline(mean_error, color="darkblue")
ax.text(mean_error, 10, f" mean={mean_error:.2g}")

fig.show()

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(
/usr/local/lib/python3.10/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
  warnings.warn(

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
File <timed exec>:6

Cell In[2], line 11, in dml1(Y, D, X)
for i, (train_idx, test_idx) in enumerate(kf.split(X)):
   # 局外関数の推定
   m = LGBMRegressor(verbose=-1).fit(X[train_idx], D[train_idx])
---> 11     l = LGBMRegressor(verbose=-1).fit(X[train_idx], Y[train_idx])
   # 残差の計算
   V_hat = D[test_idx] - m.predict(X[test_idx])

File /usr/local/lib/python3.10/site-packages/lightgbm/sklearn.py:1398, in LGBMRegressor.fit(self, X, y, sample_weight, init_score, eval_set, eval_names, eval_sample_weight, eval_init_score, eval_metric, feature_name, categorical_feature, callbacks, init_model)
def fit(  # type: ignore[override]
   self,
   X: _LGBM_ScikitMatrixLike,
   (...)
   init_model: Optional[Union[str, Path, Booster, LGBMModel]] = None,
) -> "LGBMRegressor":
   """Docstring is inherited from the LGBMModel."""
-> 1398     super().fit(
       X,
       y,
       sample_weight=sample_weight,
       init_score=init_score,
       eval_set=eval_set,
       eval_names=eval_names,
       eval_sample_weight=eval_sample_weight,
       eval_init_score=eval_init_score,
       eval_metric=eval_metric,
       feature_name=feature_name,
       categorical_feature=categorical_feature,
       callbacks=callbacks,
       init_model=init_model,
   )
   return self

File /usr/local/lib/python3.10/site-packages/lightgbm/sklearn.py:1049, in LGBMModel.fit(self, X, y, sample_weight, init_score, group, eval_set, eval_names, eval_sample_weight, eval_class_weight, eval_init_score, eval_group, eval_metric, feature_name, categorical_feature, callbacks, init_model)
evals_result: _EvalResultDict = {}
callbacks.append(record_evaluation(evals_result))
-> 1049 self._Booster = train(
   params=params,
   train_set=train_set,
   num_boost_round=self.n_estimators,
   valid_sets=valid_sets,
   valid_names=eval_names,
   feval=eval_metrics_callable,  # type: ignore[arg-type]
   init_model=init_model,
   callbacks=callbacks,
)
# This populates the property self.n_features_, the number of features in the fitted model,
# and so should only be set after fitting.
#
# The related property self._n_features_in, which populates self.n_features_in_,
# is set BEFORE fitting.
self._n_features = self._Booster.num_feature()

File /usr/local/lib/python3.10/site-packages/lightgbm/engine.py:350, in train(params, train_set, num_boost_round, valid_sets, valid_names, feval, init_model, keep_training_booster, callbacks)
   booster.best_score[dataset_name][eval_name] = score
if not keep_training_booster:
--> 350     booster.model_from_string(booster.model_to_string()).free_dataset()
return booster

File /usr/local/lib/python3.10/site-packages/lightgbm/basic.py:4592, in Booster.model_to_string(self, num_iteration, start_iteration, importance_type)
string_buffer = ctypes.create_string_buffer(buffer_len)
ptr_string_buffer = ctypes.c_char_p(ctypes.addressof(string_buffer))
_safe_call(
-> 4592     _LIB.LGBM_BoosterSaveModelToString(
       self._handle,
       ctypes.c_int(start_iteration),
       ctypes.c_int(num_iteration),
       ctypes.c_int(importance_type_int),
       ctypes.c_int64(buffer_len),
       ctypes.byref(tmp_out_len),
       ptr_string_buffer,
   )
)
actual_len = tmp_out_len.value
# if buffer length is not long enough, re-allocate a buffer

KeyboardInterrupt: 

もしCross Fittingがなければ#

def estimate_without_cross_fitting(Y, D, X):
    # 局外関数の推定
    m = LGBMRegressor(max_depth=4, verbose=-1).fit(X, D)
    l = LGBMRegressor(max_depth=4, verbose=-1).fit(X, Y)
    # 残差の計算
    V_hat = D - m.predict(X)
    Y_res = Y - l.predict(X)
    # θの推定
    theta_hat = np.mean(V_hat * V_hat) ** (-1) * np.mean(V_hat * Y_res)
    return theta_hat

estimate_without_cross_fitting(Y, D, X)

4.8689337039631475

%%time
n_rep = 1000
estimation_errors = []
for i_rep in range(n_rep):
    Y, D, X = gen_data(seed=i_rep, theta=theta)
    theta_hat = estimate_without_cross_fitting(Y, D, X)
    estimation_error = theta - theta_hat
    estimation_errors.append(estimation_error)

import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.hist(estimation_errors, bins=30)
ax.set(xlabel=r"$\theta - \hat{\theta}$", title="Estimation Error (without splitting)")

mean_error = np.mean(estimation_errors)
ax.axvline(mean_error, color="darkblue")
ax.text(mean_error, 10, f" mean={mean_error:.2g}")

fig.show()

CPU times: user 2min 39s, sys: 868 ms, total: 2min 40s
Wall time: 20.3 s

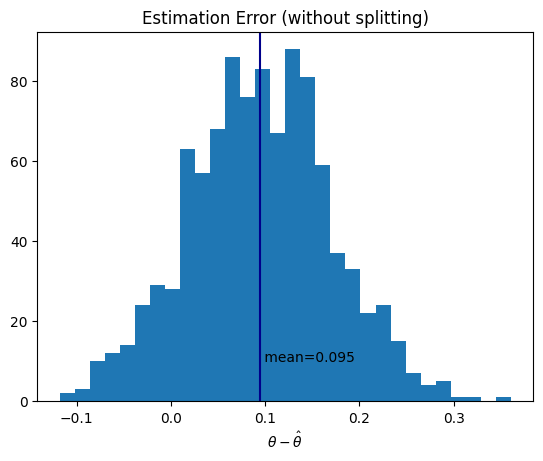
../../_images/e327772bfa14bc8467140ca332f98a821b40ca3778a634414e2bdc1754c76c9e.png

ライブラリと一致するか#

theta = 7
Y, D, X = gen_data(seed=0, theta=theta)
theta_hat = dml1(Y, D, X)
print(f"{theta=:.1f}, {theta_hat=:.3f}")

theta=7.0, theta_hat=7.002

df = pd.DataFrame(X, columns=["x"])
df["y"] = Y
df["d"] = Y
df.head()

	x	y	d
0	8.397135	99.940053	99.940053
1	7.304758	67.200958	67.200958
2	8.947698	104.094708	104.094708
3	9.699176	127.140504	127.140504
4	7.972729	91.577762	91.577762

l = LGBMRegressor(verbose=-1, n_estimators=100, max_depth=4)
m = LGBMRegressor(verbose=-1)
    
from doubleml import DoubleMLData
data = DoubleMLData(df, y_col="y", d_cols="d", x_cols=["x"])

from doubleml import DoubleMLPLR
np.random.seed(1)
dml = DoubleMLPLR(data, l, m)
dml.fit()
print(dml)

================== DoubleMLPLR Object ==================

------------------ Data summary      ------------------
Outcome variable: y
Treatment variable(s): ['d']
Covariates: ['x']
Instrument variable(s): None
No. Observations: 500

------------------ Score & algorithm ------------------
Score function: partialling out

------------------ Machine learner   ------------------
Learner ml_l: LGBMRegressor(max_depth=4, verbose=-1)
Learner ml_m: LGBMRegressor(verbose=-1)
Out-of-sample Performance:
Regression:
Learner ml_l RMSE: [[10.77148372]]
Learner ml_m RMSE: [[10.86900956]]

------------------ Resampling        ------------------
No. folds: 5
No. repeated sample splits: 1

------------------ Fit summary       ------------------
       coef   std err           t  P>|t|     2.5 %   97.5 %
d  0.989565  0.002293  431.535933    0.0  0.985071  0.99406

import numpy as np
np.random.seed(3141)
n_obs = 500
n_vars = 100
theta = 3
X = np.random.normal(size=(n_obs, n_vars))
d = np.dot(X[:, :3], np.array([5, 5, 5])) + np.random.standard_normal(size=(n_obs,))
y = theta * d + np.dot(X[:, :3], np.array([5, 5, 5])) + np.random.standard_normal(size=(n_obs,))

dml_data_sim = DoubleMLData.from_arrays(X, y, d)
print(dml_data_sim)

================== DoubleMLData Object ==================

------------------ Data summary      ------------------
Outcome variable: y
Treatment variable(s): ['d']
Covariates: ['X1', 'X2', 'X3', 'X4', 'X5', 'X6', 'X7', 'X8', 'X9', 'X10', 'X11', 'X12', 'X13', 'X14', 'X15', 'X16', 'X17', 'X18', 'X19', 'X20', 'X21', 'X22', 'X23', 'X24', 'X25', 'X26', 'X27', 'X28', 'X29', 'X30', 'X31', 'X32', 'X33', 'X34', 'X35', 'X36', 'X37', 'X38', 'X39', 'X40', 'X41', 'X42', 'X43', 'X44', 'X45', 'X46', 'X47', 'X48', 'X49', 'X50', 'X51', 'X52', 'X53', 'X54', 'X55', 'X56', 'X57', 'X58', 'X59', 'X60', 'X61', 'X62', 'X63', 'X64', 'X65', 'X66', 'X67', 'X68', 'X69', 'X70', 'X71', 'X72', 'X73', 'X74', 'X75', 'X76', 'X77', 'X78', 'X79', 'X80', 'X81', 'X82', 'X83', 'X84', 'X85', 'X86', 'X87', 'X88', 'X89', 'X90', 'X91', 'X92', 'X93', 'X94', 'X95', 'X96', 'X97', 'X98', 'X99', 'X100']
Instrument variable(s): None
No. Observations: 500

------------------ DataFrame info    ------------------
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 500 entries, 0 to 499
Columns: 102 entries, X1 to d
dtypes: float64(102)
memory usage: 398.6 KB

from doubleml import DoubleMLPLR
np.random.seed(1)
dml = DoubleMLPLR(dml_data_sim, l, m)
dml.fit()
print(dml)

================== DoubleMLPLR Object ==================

------------------ Data summary      ------------------
Outcome variable: y
Treatment variable(s): ['d']
Covariates: ['X1', 'X2', 'X3', 'X4', 'X5', 'X6', 'X7', 'X8', 'X9', 'X10', 'X11', 'X12', 'X13', 'X14', 'X15', 'X16', 'X17', 'X18', 'X19', 'X20', 'X21', 'X22', 'X23', 'X24', 'X25', 'X26', 'X27', 'X28', 'X29', 'X30', 'X31', 'X32', 'X33', 'X34', 'X35', 'X36', 'X37', 'X38', 'X39', 'X40', 'X41', 'X42', 'X43', 'X44', 'X45', 'X46', 'X47', 'X48', 'X49', 'X50', 'X51', 'X52', 'X53', 'X54', 'X55', 'X56', 'X57', 'X58', 'X59', 'X60', 'X61', 'X62', 'X63', 'X64', 'X65', 'X66', 'X67', 'X68', 'X69', 'X70', 'X71', 'X72', 'X73', 'X74', 'X75', 'X76', 'X77', 'X78', 'X79', 'X80', 'X81', 'X82', 'X83', 'X84', 'X85', 'X86', 'X87', 'X88', 'X89', 'X90', 'X91', 'X92', 'X93', 'X94', 'X95', 'X96', 'X97', 'X98', 'X99', 'X100']
Instrument variable(s): None
No. Observations: 500

------------------ Score & algorithm ------------------
Score function: partialling out

------------------ Machine learner   ------------------
Learner ml_l: LGBMRegressor(max_depth=4, verbose=-1)
Learner ml_m: LGBMRegressor(verbose=-1)
Out-of-sample Performance:
Regression:
Learner ml_l RMSE: [[8.69278568]]
Learner ml_m RMSE: [[2.22238082]]

------------------ Resampling        ------------------
No. folds: 5
No. repeated sample splits: 1

------------------ Fit summary       ------------------
      coef   std err          t          P>|t|     2.5 %    97.5 %
d  3.48904  0.108446  32.172982  4.214560e-227  3.276489  3.701591