直交関数展開：ベクトルと関数の交差点

まとめ

Tip

ベクトル空間上の直交基底\(\{ \boldsymbol{e}_i \}\)の線形結合\(c_0 \boldsymbol{e}_0 + c_1 \boldsymbol{e}_e + \cdots + c_n \boldsymbol{e}_n\)であらゆるベクトルを表せるのと同様に、関数においても 完備な直交関数系による近似によって任意の関数を表現できる

その近似は直交関数系\(\{\phi_i(x)\}\)の線形結合\(c_0 \phi_0(x)+c_1 \phi_1(x)+\cdots+c_n \phi_n(x)\)なので、級数（\(\sum_{i=1}^{\infty} c_i \phi_i(x)\) など）で表現できる（→フーリエ級数）

直交関数

区間 \([a, b]\) 上の関数 \(f(x), g(x)\) が

\[ \int_a^b f(x) g(x) \mathrm{d} x=0 \]

のとき 直交する という。

関数 \(\phi_0(x), \phi_1(x), \ldots, \phi_n(x)\) が互いに直交するとき、すなわち

\[ \int_a^b \phi_i(x) \phi_j(x) \mathrm{d} x=0, \quad i \neq j \]

のとき、これらは区間\([a,b]\)上の 直交関数系 であるという。とくに\(\phi_i(x)\)が\(x\)の多項式なら、これを 直交多項式 という。

直交多項式の例：ルジャンドルの多項式

次の関数 \(P_n(x), n=0,1,2, \ldots\), は \(n\) 次の ルジャンドルの多項式 と呼ばれる。

\[\begin{split} \begin{aligned} P_0(x) &= 1 \\ P_1(x) &= x \\ P_2(x) &= \frac{1}{2}\left(3 x^2-1\right) \\ P_3(x) &= \frac{1}{2}\left(5 x^3-3 x\right) \\ P_4(x) &= \frac{1}{8}\left(35 x^4-30 x^2+3\right) \\ P_5(x) &= \frac{1}{8}\left(63 x^5-70 x^3+15 x\right) \\ P_6(x) &= \frac{1}{16}\left(231 x^6-315 x^4+105 x^2-5\right)\\ & \vdots \end{aligned} \end{split}\]

これらは区間 \([-1,1]\) 上の直交関数系であり, 次の直交関係が成立する.

\[\begin{split} \int_{-1}^1 P_n(x) P_m(x) \mathrm{d} x= \begin{cases}\frac{2}{2 n+1} & n=m \text { のとき } \\ 0 & n \neq m \text { のとき }\end{cases} \end{split}\]

\(P_n(x)\) の一般式が次式で表せることが知られている（ロドリゲスの公式）.

\[ P_n(x)=\frac{1}{2^n n!} \frac{\mathrm{d}^n\left(x^2-1\right)^n}{\mathrm{~d} x^n} \]

直交関数の例

\[ \frac{1}{2}, \cos k x, \sin k x,\quad k=1,2,3, \ldots \]

は区間 \([-\pi, \pi]\) 上の直交関数である。

（証明） \(\cos k x, \sin k x, k=1,2,3, \ldots\) は周期 \(2 \pi\) の周期関数であるから、 1 周期 に渡る積分 \(\int_{-\pi}^\pi \cos k x \mathrm{~d} x, \int_{-\pi}^\pi \sin k x \mathrm{~d} x\) は 0 である。このことから \(\frac{1}{2}\) と \(\cos k x\), \(\sin k x\) に対して次のようになる。

\[ \int_{-\pi}^\pi \frac{1}{2} \cos k x \mathrm{~d} x=\int_{-\pi}^\pi \frac{1}{2} \sin k x \mathrm{~d} x=0 \]

\(\cos k x, \sin l x\) に対しては次のようになる。

\[ \int_{-\pi}^\pi \cos k x \sin l x \mathrm{~d} x=\frac{1}{2} \int_{-\pi}^\pi(\sin (k+l) x-\sin (k-l) x) \mathrm{d} x=0 \]

\(k \neq l\) のとき \(\cos k x, \cos l x\) に対して次のようになる。

\[ \int_{-\pi}^\pi \cos k x \cos l x \mathrm{~d} x=\frac{1}{2} \int_{-\pi}^\pi(\cos (k+l) x+\cos (k-l) x) \mathrm{d} x=0 \]

\(k \neq l\) のとき \(\sin k x, \sin l x\) に対して次のようになる。

\[ \int_{-\pi}^\pi \sin k x \sin l x \mathrm{~d} x=-\frac{1}{2} \int_{-\pi}^\pi(\cos (k+l) x-\cos (k-l) x) \mathrm{d} x=0 \]

以上より \(\frac{1}{2}, \cos k x, \sin k x, k=1,2,3, \ldots\), が直交関数系であることが示された。

また次の関係も成り立つ。

\[\begin{split} \begin{gathered} \int_{-\pi}^\pi\left(\frac{1}{2}\right)^2 \mathrm{~d} x=\frac{\pi}{2} \\ \int_{-\pi}^\pi \cos ^2 k x \mathrm{~d} x=\frac{1}{2} \int_{-\pi}^\pi(1+\cos 2 k x) \mathrm{d} x=\pi \\ \int_{-\pi}^\pi \sin ^2 k x \mathrm{~d} x=\frac{1}{2} \int_{-\pi}^\pi(1-\cos 2 k x) \mathrm{d} x=\pi \end{gathered} \end{split}\]

最小二乗近似

区間\([a,b]\)上の直交関数系\(\{\phi_i(x)\}, i=0,1,\cdots,n\)の線形結合で関数\(f(x)\)を近似する事を考える

\[ f(x) \approx c_0 \phi_0(x)+c_1 \phi_1(x)+\cdots+c_n \phi_n(x) \]

このような近似は、画像や音声を表す信号を少量の数値のみで高速に伝送したり、メモリの記憶容量を削減するために用いられる。

近似の尺度として最小二乗法

\[ J=\frac{1}{2} \int_a^b\left(f(x)-c_0 \phi_0(x)-c_1 \phi_1(x)-\cdots-c_n \phi_n(x)\right)^2 \mathrm{~d} x \]

\[ \min_{c_0,\cdots,c_n} J \]

を用いると、各係数\(c_i\)は

\[ c_i=\frac{\int_a^b f(x) \phi_i(x) \mathrm{d} x}{\int_a^b \phi_i(x)^2 \mathrm{~d} x}, \quad i=0,1, \ldots, n \]

となる

証明

\[\begin{split} \begin{aligned} \frac{\partial J}{\partial c_i}= & -\int_a^b\left(f(x)-c_0 \phi_0(x)-c_1 \phi_1(x)-\cdots-c_n \phi_n(x)\right) \phi_i(x) \mathrm{d} x \\ = & -\left(\int_a^b f(x) \phi_i(x) \mathrm{d} x-c_0 \int_a^b \phi_0(x) \phi_i(x) \mathrm{d} x\right. \\ & \left.\quad-c_1 \int_a^b \phi_1(x) \phi_i(x) \mathrm{d} x-\cdots-c_n \int_a^b \phi_n(x) \phi_i(x) \mathrm{d} x\right) \\ & =-\left(\int_a^b f(x) \phi_i(x) \mathrm{d} x-c_i \int_a^b \phi_i(x)^2 \mathrm{~d} x\right) \end{aligned} \end{split}\]

これを0とおくと、係数が求まる

完備

定義（完備）

直交関数系の無限列 \(\left\{\phi_i\right\}, i=0,1,2, \cdots\) があり、任意の連続関数 \(f(x)\) の \(\phi_0(x), \phi_1(x), \phi_2(x), \cdots, \phi_n(x)\) による近似が \(n \rightarrow \infty\) のときに \(f(x)\) に収束するとき、 直交関数系 \(\left\{\phi_i\right\}\) は 完備 (complete) であるといい、 その収束する級数を関数 \(f(x)\) の \(\left\{\phi_i\right\}\) による 直交関数展開 という。

フーリエ級数

\[ \frac{1}{2}, \cos k x, \sin k x,\quad k=1,2,3, \ldots \]

は区間\([-\pi,\pi]\)上で完備であることが知られ、これらを用いる直交関数展開を フーリエ級数 (Fourier series) という。

関数\(f(x)\)の近似

\[ f(x) \approx \frac{a_0}{2}+a_1 \cos x+b_1 \sin x+a_2 \cos 2 x+b_2 \sin 2 x+a_3 \cos 3 x+b_3 \sin 3 x+\cdots \]

の係数\(a_n, b_n\)は次のようになる

\[ a_0=\frac{1}{\pi} \int_{-\pi}^\pi f(x) \mathrm{d} x, \quad a_k=\frac{1}{\pi} \int_{-\pi}^\pi f(x) \cos k x \mathrm{~d} x, \quad b_k=\frac{1}{\pi} \int_{-\pi}^\pi f(x) \sin k x \mathrm{~d} x \]

これらの係数を フーリエ係数 と呼ぶ。

例（フーリエ級数）

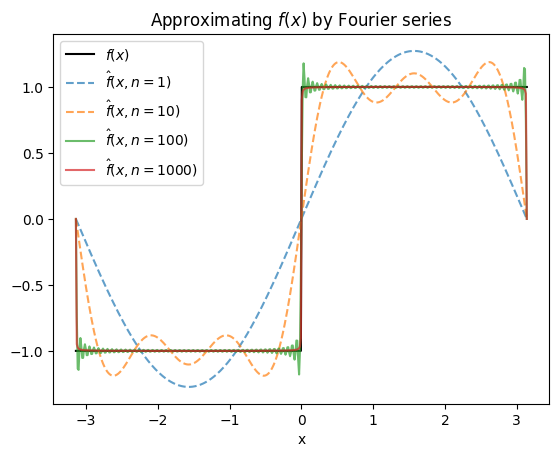
次の関数 \(f(x)\) を区間 \([-\pi, \pi]\) 上でフーリエ級数に展開せよ

\[\begin{split} f(x)=\begin{cases} 1 & 0 \leq x \leq \pi \text { のとき } \\ -1 & -\pi \leq x<0 \text { のとき } \end{cases} \end{split}\]

\[\begin{split} \begin{aligned} a_0 & =\frac{1}{\pi}\left(-\int_{-\pi}^0 \mathrm{~d} x+\int_0^\pi \mathrm{d} x\right)=\frac{-\pi+\pi}{\pi}=0 \\ a_k & =\frac{1}{\pi}\left(-\int_{-\pi}^0 \cos k x \mathrm{~d} x+\int_0^\pi \cos k x \mathrm{~d} x\right) \\ & =\frac{1}{\pi}\left(-\left[\frac{\sin k x}{k}\right]_{-\pi}^0+\left[\frac{\sin k x}{k}\right]_0^\pi\right)=0 \\ b_k & =\frac{1}{\pi}\left(-\int_{-\pi}^0 \sin k x \mathrm{~d} x+\int_0^\pi \sin k x \mathrm{~d} x\right)=\frac{1}{\pi}\left(\left[\frac{\cos k x}{k}\right]_{-\pi}^0-\left[\frac{\cos k x}{k}\right]_0^\pi\right) \\ & =\frac{1}{\pi}\left(\frac{1-\cos (-\pi) k}{k}-\frac{\cos \pi k-1}{k}\right)=\frac{2\left(1-(-1)^k\right)}{k \pi} \end{aligned} \end{split}\]

よって、次のようになる

\[ f(x)=\frac{4}{\pi} \sin x+\frac{4}{3 \pi} \sin 3 x+\frac{4}{5 \pi} \sin 5 x+\frac{4}{7 \pi} \sin 7 x+\cdots \]

この近似を \(\hat{f}(x, n) = \sum_{k=1}^n b_k \cdot \sin kx\) とおく。pythonで計算すると次の図のようになる

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

def f(x: np.array) -> np.array:
    y = np.zeros_like(x)
    y[(0 <= x) & (x <= np.pi)] = 1
    y[(-np.pi <= x) & (x < 0)] = -1
    return y

# a_0, a_k が 0なので、 b_k （sinの係数）のみが残る
def b(k):
    return (2 * (1 - (-1)**k)) / (k * np.pi)

def f_hat(x: np.array, n: int) -> np.array:
    approx = np.zeros_like(x)
    for k in range(1, n+1):
        approx += b(k) * np.sin(k * x)
    return approx


fig, ax = plt.subplots()
x = np.linspace(-np.pi, np.pi, 500)
ax.plot(x, f(x), label="$f(x)$", color="black")
ax.plot(x, f_hat(x, n=1), label=r"$\hat{f}(x, n=1)$", linestyle="--", alpha=0.7)
ax.plot(x, f_hat(x, n=5), label=r"$\hat{f}(x, n=5)$", linestyle="--", alpha=0.7)
ax.plot(x, f_hat(x, n=100), label=r"$\hat{f}(x, n=100)$", linestyle="--", alpha=0.7)
ax.plot(x, f_hat(x, n=1000), label=r"$\hat{f}(x, n=1000)$", linestyle="--", alpha=0.7)
ax.set(xlabel="x", title=r"Approximating $f(x)$ by Fourier series")
ax.legend()
fig.show()

直交展開

計量空間の元 \(e_1, e_2, \ldots, e_n\) が互いに直交するとき、すなわち

\[ \left(\boldsymbol{e}_i, \boldsymbol{e}_j\right)=0, \quad i \neq j \]

のとき、これらは 直交系 であるという。 特に、すべてがノルム \(1\left(\left\|\boldsymbol{e}_i\right\|=1\right.\), \(i=1, \ldots, n)\) のとき、これを 正規直交系 という。 式で書くと次のようになる。

\[ \left(\boldsymbol{e}_i, \boldsymbol{e}_j\right)=\delta_{i j} \]

ただし\(\delta_{i j}\)はクロネッカーのデルタである

線形結合による表現

計量空間\(L\)の直交系\(\{\boldsymbol{e}_i \}, i=1,\dots, n\)を用いて、任意の元\(u\in L\)を線形結合で

\[ \boldsymbol{u} \approx c_1 \boldsymbol{e}_1+c_2 \boldsymbol{e}_2+\cdots+c_n \boldsymbol{e}_n \]

と近似することを考える。

二乗誤差

\[ J=\frac{1}{2}\left\|\boldsymbol{u}-\left(c_1 \boldsymbol{e}_1+c_2 \boldsymbol{e}_2+\cdots+c_n \boldsymbol{e}_n\right)\right\|^2 \]

を用いて最小二乗法で近似すると、解は

\[ c_i=\frac{\left(\boldsymbol{u}, \boldsymbol{e}_i\right)}{\left\|\boldsymbol{e}_i\right\|^2} \quad i=1,\dots, n \]

となる。

証明

\[\begin{split} \begin{aligned} J &= \frac{1}{2} \left\|\boldsymbol{u}-\left(c_1 \boldsymbol{e}_1+c_2 \boldsymbol{e}_2+\cdots+c_n \boldsymbol{e}_n\right)\right\|^2 \\ &= \frac{1}{2} \left\|\boldsymbol{u}- \sum^n_{j=1} c_j \boldsymbol{e}_j \right\|^2 \\ &= \frac{1}{2} \left ( \boldsymbol{u}- \sum^n_{j=1} c_j \boldsymbol{e}_j, \boldsymbol{u}- \sum^n_{j=1} c_j \boldsymbol{e}_j \right) \end{aligned} \end{split}\]

内積の微分は

\[ \frac{d}{d x} \langle \boldsymbol{f}(x), \boldsymbol{g}(x) \rangle = \left \langle \frac{d \boldsymbol{f}(x)}{d x}, \boldsymbol{g}(x) \right \rangle +\left \langle \boldsymbol{f}(x), \frac{d \boldsymbol{g}(x)}{d x}\right \rangle \]

となるため、

\[\begin{split} \begin{aligned} \frac{\partial J}{\partial c_i} &=\frac{1}{2} \frac{\partial}{\partial c_i}\left(\boldsymbol{u}-\sum_{j=1}^n c_j \boldsymbol{e}_j, \boldsymbol{u}-\sum_{k=1}^n c_k \boldsymbol{e}_k\right) \\ &=\frac{1}{2}\left(-\boldsymbol{e}_i, \boldsymbol{u}-\sum_{j=1}^n c_j \boldsymbol{e}_j\right) +\frac{1}{2}\left(\boldsymbol{u}-\sum_{j=1}^n c_j \boldsymbol{e}_j,-\boldsymbol{e}_i\right) \\ &=\left(\boldsymbol{u}-\sum_{j=1}^n c_j \boldsymbol{e}_j,-\boldsymbol{e}_i\right) \quad (\because 内積の対称性) \\ &= \left(\boldsymbol{u}, -\boldsymbol{e}_i\right) - \left(\sum_{j=1}^n c_j \boldsymbol{e}_j, -\boldsymbol{e}_i\right) \quad \because内積の線形性\\ &= \left(\sum_{j=1}^n c_j \boldsymbol{e}_j, \boldsymbol{e}_i\right) -\left(\boldsymbol{u}, \boldsymbol{e}_i\right)\\ &= \sum_{j=1}^n c_j \left(\boldsymbol{e}_j, \boldsymbol{e}_i\right) -\left(\boldsymbol{u}, \boldsymbol{e}_i\right) \quad \because内積の線形性\\ & =\sum_{j=1}^n c_j \delta_{i j}\left\|\boldsymbol{e}_j\right\|^2-\left(\boldsymbol{u}, \boldsymbol{e}_i\right) \\ &=c_i\left\|\boldsymbol{e}_i\right\|^2-\left(\boldsymbol{u}, \boldsymbol{e}_i\right) \end{aligned} \end{split}\]

これを0とおいて解くと求まる

\[\begin{split} c_i \|\boldsymbol{e}_i\|^2 - (\boldsymbol{u}, \boldsymbol{e}_i) = 0 \\ \iff c_i \|\boldsymbol{e}_i\|^2 = (\boldsymbol{u}, \boldsymbol{e}_i)\\ \iff c_i = \frac{ (\boldsymbol{u}, \boldsymbol{e}_i) }{ \|\boldsymbol{e}_i\|^2 }\\ \end{split}\]

参考：内積の微分

内積の微分は

\[ \boldsymbol{f}(x) = (f_1(x), \cdots, f_n(x)) \boldsymbol{g}(x) = (g_1(x), \cdots, g_n(x)) \]

とすると

\[\begin{split} \begin{aligned} \frac{d}{d x} \langle \boldsymbol{f}(x), \boldsymbol{g}(x) \rangle &= \frac{d}{d x} \left( \sum_{i=1}^n f_i(x) g_i(x) \right)\\ &= \sum_{i=1}^n \frac{d}{d x} \left( f_i(x) g_i(x) \right)\\ &= \sum_{i=1}^n \left( \frac{d f_i(x)}{d x} g_i(x) + f_i(x) \frac{d g_i(x)}{d x} \right) \quad (積の微分公式) \\ &= \sum_{i=1}^n \frac{d f_i(x)}{d x} g_i(x) + \sum_{i=1}^n f_i(x) \frac{d g_i(x)}{d x} \\ &= \left \langle \frac{d \boldsymbol{f}(x)}{d x}, \boldsymbol{g}(x) \right \rangle +\left \langle \boldsymbol{f}(x), \frac{d \boldsymbol{g}(x)}{d x}\right \rangle \end{aligned} \end{split}\]

となる

大学物理のフットノート|物理数学|ベクトルの微分公式(基本編)

計量空間\(L\)の直交系\(\{\boldsymbol{e}_i \}, i=1,\dots, n\)を用いて、任意の元\(u\in L\)を線形結合で等号で

\[ \boldsymbol{u} = c_1 \boldsymbol{e}_1+c_2 \boldsymbol{e}_2+\cdots+c_n \boldsymbol{e}_n \]

と表される場合に、係数\(c_i\)は最小二乗法による近似と同じ解

\[ c_i = \frac{ (\boldsymbol{u}, \boldsymbol{e}_i) }{ \|\boldsymbol{e}_i\|^2 } \]

になる

証明

\[ \boldsymbol{u} = c_1 \boldsymbol{e}_1 + \cdots + c_n \boldsymbol{e}_n \]

の両辺と\(\boldsymbol{e}_i\)の内積をとると、

\[\begin{split} \begin{aligned} (\boldsymbol{u}, \boldsymbol{e}_i) &= c_1 (\boldsymbol{e}_1, \boldsymbol{e}_i) + \cdots + c_n (\boldsymbol{e}_n, \boldsymbol{e}_i)\\ &= c_i (\boldsymbol{e}_i, \boldsymbol{e}_i)\\ &= c_i \| \boldsymbol{e}_i \|^2\\ \end{aligned} \end{split}\]

よって

\[ c_i = \frac{ (\boldsymbol{u}, \boldsymbol{e}_i) }{ \|\boldsymbol{e}_i\|^2 } \]

直交射影

元\(\boldsymbol{u}\)を直交系\(\boldsymbol{e}_1, \boldsymbol{e}_2, \ldots, \boldsymbol{e}_n\)の線形結合の集合\(\mathcal{V}_n\)（\(\{\boldsymbol{e}_i\}\)の張る部分空間）で近似することを考える。

\[ \boldsymbol{u} \approx c_1 \boldsymbol{e}_1+c_2 \boldsymbol{e}_2+\cdots+c_n \boldsymbol{e}_n \]

最小二乗近似したものは

\[ c_i = \frac{ (\boldsymbol{u}, \boldsymbol{e}_i) }{ \|\boldsymbol{e}_i\|^2 } \]

より

\[ \hat{\boldsymbol{u}} = \sum_{i=1}^n \frac{ (\boldsymbol{u}, \boldsymbol{e}_i) }{ \|\boldsymbol{e}_i\|^2 } \boldsymbol{e}_i \]

と書くことができる。\(\hat{\boldsymbol{u}}\)の幾何学的な解釈としては、\(\boldsymbol{u}\)から\(\{\boldsymbol{e}_i\}\)の張る部分空間へと下ろした「垂線の足」となる。 このことから、\(\hat{\boldsymbol{u}}\)は\(\{\boldsymbol{e}_i\}\)の張る部分空間\(\mathcal{V}_n\)への （直交）射影 と呼ぶ。

直交基底

直交系\(\boldsymbol{e}_1, \boldsymbol{e}_2, \ldots, \boldsymbol{e}_n\)（\(n=\infty\)でもよい）による、計量空間\(\mathcal{L}\)の元\(\boldsymbol{u}\)の最小二乗近似\(\hat{\boldsymbol{u}}\)が\(\boldsymbol{u}\)に一致するとき（\(n=\infty\)のときは\(n\to \infty\)で\(\boldsymbol{u}\)に収束するとき）、\(\{\boldsymbol{e}_i\}\)は\(\mathcal{L}\)の 直交基底 であるという。

このとき\(\mathcal{L}\)は \(n\)次元計量空間 （\(n=\infty\)なら 無限次元計量空間 ）であるという。

直交基底の線形結合で表すことを 直交展開 という。

直交基底の例：ルジャンドルの多項式

ルジャンドルの多項式\(P_n(x)\)

\[ P_n(x)=\frac{1}{2^n n!} \frac{\mathrm{d}^n\left(x^2-1\right)^n}{\mathrm{~d} x^n} \]

は区間\([-1,1]\)上の連続関数の直交基底である

\[\begin{split} \int_{-1}^1 P_n(x) P_m(x) \mathrm{d} x= \begin{cases}\frac{2}{2 n+1} & n=m \text { のとき } \\ 0 & n \neq m \text { のとき }\end{cases} \end{split}\]

パーセバルの式

\(\mathcal{L}\)を計量空間とする。\(\boldsymbol{u}, \boldsymbol{v} \in \mathcal{L}\)について、正規直交基底\(\{\boldsymbol{e}_i\}, i=1,\dots,n\)で

\[\begin{split} \begin{aligned} \boldsymbol{u}&=c_1 \boldsymbol{e}_1+c_2 \boldsymbol{e}_2+\cdots+c_n \boldsymbol{e}_n \\ \boldsymbol{v}&=d_1 \boldsymbol{e}_1+d_2 e_2+\cdots+d_n \boldsymbol{e}_n \end{aligned} \end{split}\]

と表したとする。このとき、次の パーセバル（・プランシュレル）の式 が成り立つ（\(n=\infty\)でも成り立つ）

\[ (\boldsymbol{u}, \boldsymbol{v})=\sum_{i=1}^n c_i d_i, \quad\|\boldsymbol{u}\|^2=\sum_{i=1}^n c_i^2 \]

証明

\[\begin{split} \begin{aligned} (\boldsymbol{u}, \boldsymbol{v}) &= \left( \sum_{i=1}^n c_i \boldsymbol{e}_i, \sum_{j=1}^n d_j \boldsymbol{e}_j \right)\\ &= \sum_{i=1}^n c_i \left( \boldsymbol{e}_i, \sum_{j=1}^n d_j \boldsymbol{e}_j \right) \quad (\because 内積の線形性)\\ &= \sum_{i=1}^n \sum_{j=1}^n c_i d_j \left( \boldsymbol{e}_i, \boldsymbol{e}_j \right) \quad (\because 内積の線形性)\\ &= \sum_{i=1}^n \sum_{j=1}^n c_i d_j \delta_{ij} \quad (\because \boldsymbol{e}は 正規直交基底)\\ &= \sum_{i=1}^n c_i d_i \end{aligned} \end{split}\]

\[\begin{split} \begin{aligned} \|\boldsymbol{u}\|^2 &= (\boldsymbol{u}, \boldsymbol{u})\\ &= (\sum_{i=1}^n c_i \boldsymbol{e}_i, \sum_{j=1}^n c_j \boldsymbol{e}_j)\\ &= \sum_{i=1}^n \sum_{j=1}^n c_i c_j (\boldsymbol{e}_i, \boldsymbol{e}_j)\\ &= \sum_{i=1}^n \sum_{j=1}^n c_i c_j \delta_{ij}\\ &= \sum_{i=1}^n c_i^2\\ \end{aligned} \end{split}\]

参考

金谷健一. (2003). これなら分かる応用数学教室: 最小二乗法からウェーブレットまで.