FWL定理#
FWL定理
目的変数のベクトル\(Y \in \mathbb{R}^{n\times 1}\)、説明変数の行列\(X \in \mathbb{R}^{n\times d}\)と誤差項\(e \in \mathbb{R}^{n\times 1}\)による線形回帰モデル
があるとする。
説明変数を\(X = (X_1 | X_2)\)と2つのグループに分割し、回帰係数ベクトル\(\beta\)も合わせて\(\beta = (\beta_1 | \beta_2)^T\)と2つに分割して
と表す。
この回帰モデルの\(\beta_1\)は、残差回帰(residual regression)と呼ばれる以下の手順に従うことでも得ることができる。
\(X_1\)を\(X_2\)に回帰して残差\(\tilde{X}_1\)を得る:\(\tilde{X}_1 = X_1 - X_2 \hat{\delta}\)
\(Y\)を\(X_2\)に回帰して残差\(\tilde{Y}\)を得る:\(\tilde{Y} = Y - X_2 \hat{\gamma}\)
\(\tilde{Y}\)を\(\tilde{X}_1\)に回帰させる:\(\tilde{Y} = \tilde{X}_1 \beta_1\)
証明#
残差への回帰\(\tilde{Y} = \tilde{X}_1 \beta_1\)は
であり、
を代入するとそれぞれ
となる。
これらをそれぞれ被説明変数、説明変数として最小二乗推定すると
(\(I - X_2 (X_2^T X_2)^{-1} X_2^T\)は冪等で対称な行列のため2行目で計算が簡略化できている)
次に、すべての説明変数\(X\)を\(Y\)に回帰したとき
の\(X_1\)の係数\(\beta_1\)の推定量を求める。二乗誤差の最小化の解
の1階の条件は
となる。\(\hat{\beta}_2\)を消すためには、2つ目の式に左から\(-X_1^T X_2(X_2^T X_2)^{-1}\)を掛けて
これを第1式に足すと
となる。
これを変形すると
となり、残差回帰の解と一致する。
数値例#
import numpy as np
n = 100
d = 4
k = 1
np.random.seed(0)
beta = np.array(list(range(1, d + 1)))
print(f"{beta=}")
X = np.random.uniform(size=(n, d))
e = np.random.normal(size=n) * 0.1
Y = X @ beta + e
X1 = X[:, :k]
X2 = X[:, k:]
beta1 = beta[:k]
beta2 = beta[k:]
assert np.allclose(Y, X1 @ beta1 + X2 @ beta2 + e)
beta=array([1, 2, 3, 4])
# I - X_2 (X_2^T X_2)^{-1} X_2^T は冪等で対称な行列
I = np.eye(n)
M = (I - X2 @ np.linalg.inv(X2.T @ X2) @ X2.T)
assert np.allclose(M.T, M)
assert np.allclose(M, M @ M)
delta = np.linalg.inv(X2.T @ X2) @ X2.T @ X1
gamma = np.linalg.inv(X2.T @ X2) @ X2.T @ Y
Y_tilde = (Y - X2 @ gamma)
X_tilde = (X1 - X2 @ delta)
# 残差回帰
beta_hat2 = np.linalg.inv(X_tilde.T @ X_tilde) @ X_tilde.T @ Y_tilde
beta_hat2.round(1)
array([1.])
# 通常の線形回帰
beta_hat1 = np.linalg.inv(X.T @ X) @ X.T @ Y
beta_hat1.round(1)
array([1. , 2. , 2.9, 4. ])
残差の作図#

外生性・直交条件からの説明#
浅野・中村では誤差が直交することから証明するスタイルで、有斐閣の本はより直接的に証明している
OLSのPartialling out解釈#
というモデルの\(\beta_1\)は
\(y\)を\(x_1\)に回帰する:\(y = \beta_0 + \beta_1 x_1 + \beta_2 z_2 + \varepsilon\)
\(y\)を\(\tilde{x}_1\)に回帰する(ここで\(\tilde{x}_1\)は\(x_1\)を\(x_2\)に回帰した残差)
\(\tilde{y}\)を\(\tilde{x}_1\)に回帰する(ここで\(\tilde{y}\)は\(y\)を\(x_2\)に回帰した残差)
の3つの方法のいずれかで推定することができる
数値例#
import numpy as np
n = 1000
np.random.seed(0)
x0 = np.ones(shape=(n, ))
x2 = np.random.uniform(0, 1, size=n)
x1 = 3 * x2 + np.random.uniform(0, 1, size=n) + np.random.normal(0, 1, size=n)
X = np.array([ x0, x1, x2 ]).T
e = np.random.normal(0, 1, size=n)
beta = np.array([10, 5, 7]) # 真のbeta
y = X @ beta + e
np.corrcoef(X, rowvar=False)
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/numpy/lib/function_base.py:2897: RuntimeWarning: invalid value encountered in divide
c /= stddev[:, None]
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/numpy/lib/function_base.py:2898: RuntimeWarning: invalid value encountered in divide
c /= stddev[None, :]
array([[ nan, nan, nan],
[ nan, 1. , 0.64601675],
[ nan, 0.64601675, 1. ]])
class OLS:
def fit(self, X, y):
self.beta_ = np.linalg.inv(X.T @ X) @ X.T @ y
return self
def predict(self, X):
return X @ self.beta_
1. \(y\)を\(x_1\)に回帰する#
\(y = \beta_0 + \beta_1 x_1 + \beta_2 z_2 + \varepsilon\)
# 1. 𝑦 を 𝑥1 に回帰する
OLS().fit(X, y).beta_
array([9.98226817, 5.03640436, 6.80111723])
2. \(y\)を\(\tilde{x}_1\)に回帰する#
ここで\(\tilde{x}_1\)は\(x_1\)を\(x_2\)に回帰した残差
# 2. 𝑦 を 𝑥̃ 1 に回帰する
X_ = X[:, [0, 2]] # x0, x2だけのX
x1_res = x1 - OLS().fit(X_, x1).predict(X_)
# 切片を付けた場合
X_ = np.array([ x0, x1_res ]).T
OLS().fit(X_, y).beta_
array([23.29878836, 5.03640436])
# 切片を付けない場合
OLS().fit(x1_res.reshape(-1, 1), y).beta_
array([5.03640436])
3. \(\tilde{y}\)を\(\tilde{x}_1\)に回帰する#
ここで\(\tilde{y}\)は\(y\)を\(x_2\)に回帰した残差
# 3. 𝑦̃ を 𝑥̃ 1 に回帰する
X_ = X[:, [0, 2]] # x0, x2だけのX
y_res = y - OLS().fit(X_, y).predict(X_)
# 切片を付けない場合
OLS().fit(x1_res.reshape(-1, 1), y_res).beta_
array([5.03640436])
# 切片を付けた場合
X_ = np.array([ x0, x1_res ]).T
OLS().fit(X_, y_res).beta_
array([8.32667268e-17, 5.03640436e+00])
partialling out#
OLS推定では説明変数と残差の共分散はゼロになる。
というモデルがあったとき、説明変数\(x_j\)を他のすべての説明変数に回帰すると、その残差\(\tilde{x}_j\)は説明変数\(x_j\)の分散の情報を残す一方で他の説明変数とは無相関になる。
したがって\(y\)をこの残差\(\tilde{x}_j\)に回帰すると、その回帰係数\(\beta_j\)は\(y\)に対する\(x_j\)の影響のみを示す。
→他の変数の影響を排除(partialling out)できる
FWL定理の応用#
データの可視化#
元のモデルに\(d\)次元の説明変数があったとしても、\(\tilde{x}_j\)と\(y\)の関係へと次元を削減することができるため、グラフに表示しやすい。
statsmodelsで簡単に実行できる#
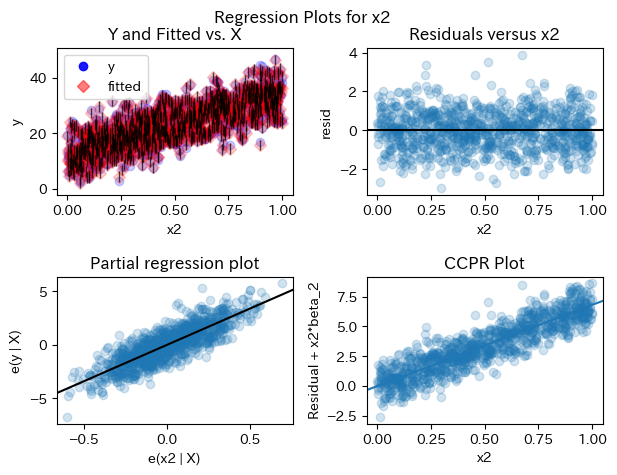
statsmodelsのplot_regress_exog関数は残差の分析に関する4つの図をまとめて出力でき、そのうちのひとつ「Partial regression plot」がpartialling outした残差同士の散布図になっている。
import statsmodels.api as sm
results = sm.OLS(y, X).fit()
fig = sm.graphics.plot_regress_exog(results, 'x2')
計算の高速化#
PyHDFEパッケージのような高次元データの分析において活用されているらしい
統計的因果推論#
Belloni et al. (2014)のpost-double selection
Chernozhukov et al. (2018)のDouble/debiased machine learning (DML)
などで用いられる。DMLはモデルの学習アルゴリズムに機械学習を許容するので、過学習や正則化によるバイアスに対処するためのcross-fittingという推定方法を提案している。
歴史:Yule-Frisch-Waugh-Lovell Theorem#
[2307.00369] The Yule-Frisch-Waugh-Lovell Theorem
FWLの前にYuleがいたらしい
通常、Frisch and Waugh (1933) と Lovell (1963) の名前をとって Frisch-Waugh-Lovell Theoremと呼ぶ。しかしこの論文によれば Yule (1907) も重要な貢献をしており、計量経済学では知名度がないものの統計学分野では注目されているため、FWL定理ではなくYFWL定理と呼ぶことを提案している。
参考文献#
FWL
Frisch, R., & Waugh, F. V. (1933). Partial time regressions as compared with individual trends. Econometrica: Journal of the Econometric Society, 387-401.
Lovell, M. C. (1963). Seasonal adjustment of economic time series and multiple regression analysis. Journal of the American Statistical Association, 58(304), 993-1010.
(考察)再帰的なpartialling outで任意のパラメータを任意の次元で推定できないか?#
→ できなかった
うまくいってAdditive modelとのつながりが見えれば面白かったんだが
import numpy as np
# データを生成
n = 1000
np.random.seed(0)
x0 = np.ones(shape=(n, ))
x2 = np.random.uniform(0, 1, size=n)
x3 = np.random.uniform(0, 1, size=n)
x1 = x2 + x3 + np.random.normal(0, 1, size=n)
X = np.array([ x0, x1, x2, x3 ]).T
e = np.random.normal(0, 1, size=n)
beta = np.array([10, 5, 7, 3]) # 真のbeta
y = X @ beta + e
class OLS:
def fit(self, X, y):
self.beta_ = np.linalg.inv(X.T @ X) @ X.T @ y
return self
def predict(self, X):
return X @ self.beta_
1. \(y\)を\(x_1\)に回帰する#
\(y = \beta_0 + \beta_1 x_1 + \beta_2 z_2 + \varepsilon\)
# 1. 𝑦 を 𝑥1 に回帰する
OLS().fit(X, y).beta_
array([9.95538609, 5.03200117, 6.87766976, 3.05740035])
2. \(y\)を\(\tilde{x}_1\)に回帰する#
ここで\(\tilde{x}_1\)は\(x_1\)を残りの説明変数に回帰した残差
# 2. 𝑦 を 𝑥̃ 1 に回帰する
X_ = X[:, [0, 2, 3]]
x1_res = x1 - OLS().fit(X_, x1).predict(X_)
# 切片を付けない場合
OLS().fit(x1_res.reshape(-1, 1), y).beta_
array([5.03200117])
import matplotlib.pyplot as plt
plt.scatter(x1_res, x1)
<matplotlib.collections.PathCollection at 0x7fa3ba08b010>

from scipy.stats import pearsonr
pearsonr(x1_res, x1).statistic.round(3)
0.933
説明変数1つずつでpartialling outできないか?
\(\tilde{x}_1 = x_1 - \hat{\beta}_0 x_0\)
\(\tilde{x}_1 = \tilde{x}_1 - \hat{\beta}_2 x_2\)
\(\tilde{x}_1 = \tilde{x}_1 - \hat{\beta}_3 x_3\)
for all nuisance parameter indices \(j \in J\)
\(\newcommand{\argmin}{\mathop{\arg\min}} \hat{\beta}_j = \argmin_{\beta_j} E[(y - \beta_j x_j)^2]\)
\(\tilde{x}_j = y - \hat{\beta}_j x_j\)
# 2. 𝑦 を 𝑥̃ 1 に回帰する
x1_res = x1.copy()
nuisance_indices = [0, 2, 3]
for i in nuisance_indices:
X_ = X[:, [i]]
x1_res = x1_res - OLS().fit(X_, x1_res).predict(X_)
print(f"corr(x1_res, x1): {pearsonr(x1_res, x1).statistic:.3f}")
print(f"beta1 : {OLS().fit(x1_res.reshape(-1, 1), y).beta_[0]:.3f}")
OLS().fit(x1_res.reshape(-1, 1), y).beta_
corr(x1_res, x1): 1.000
beta1 : 5.750
corr(x1_res, x1): 0.998
beta1 : 3.435
corr(x1_res, x1): 0.998
beta1 : 2.925
array([2.92542108])
# 2. 𝑦 を 𝑥̃ 1 に回帰する
x1_res = x1.copy()
nuisance_indices = [0, 2, 3]
for i in nuisance_indices[::-1]:
X_ = X[:, [i]]
x1_res = x1_res - OLS().fit(X_, x1_res).predict(X_)
print(f"corr(x1_res, x1): {pearsonr(x1_res, x1).statistic:.3f}")
print(f"beta1 : {OLS().fit(x1_res.reshape(-1, 1), y).beta_[0]:.3f}")
OLS().fit(x1_res.reshape(-1, 1), y).beta_
corr(x1_res, x1): 0.887
beta1 : 7.193
corr(x1_res, x1): 0.876
beta1 : 2.998
corr(x1_res, x1): 0.876
beta1 : 4.613
array([4.61310126])