フーリエ解析
フーリエ解析(Fourier analysis):信号を異なる周波数の正弦波(sin)の重ね合わせとして表現すること
例えば画像を周波数の表現にして、周波数をフーリエ解析で分解したりする。
フーリエ級数
幅\(T\)の区間\([-T/2, T/2]\)における連続関数\(f(t)\)はフーリエ級数に展開できる
\[
f(t)=\frac{a_0}{2}+\sum_{k=1}^{\infty}\left(a_k \cos k \omega_o t+b_k \sin k \omega_o t\right), \quad-\frac{T}{2} \leq t \leq \frac{T}{2}
\]
フーリエ係数は
\[
a_k=\frac{2}{T} \int_{-T / 2}^{T / 2} f(t) \cos k \omega_o t \mathrm{~d} t, \quad b_k=\frac{2}{T} \int_{-T / 2}^{T / 2} f(t) \sin k \omega_o t \mathrm{~d} t
\]
である。
ここで
\[
\omega_o=\frac{2 \pi}{T}
\]
である。これを 基本周波数 といい、フーリエ級数は関数\(f(t)\)を\(\omega_o\)の整数倍の周波数の正弦波の重ね合わせとして表現する。
\(a_0/2\)を 直流成分 と呼び、\(\omega_o\)の\(k\)倍の周波数の振動を第\(k\) 高調波 と呼ぶ。以下では\(t\)を「時刻」とみなし、\(f(t)\)を「信号」と呼ぶ。
Tip
基本周波数 \(\omega_0 = 2\pi / T\)は、幅\(T\)、区間\([-2/T, 2/T]\)を1周期とする振動の周波数である。
例えば\(\sin(x)\)は1周期が\(2\pi\)なので\(\omega_0 = 1\)となる
複素数の指数関数
複素数
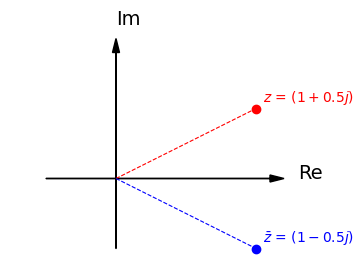
複素数とは \(z=x+i y\) のように 実(数)部 \(x\) に 虚(数)部 \(y\) の \(i\) 倍を足したもの
\(i\) は 虚数単位 と呼ばれ、 \(i^2=-1\) となる数と約束したもの。
\(x\)軸を実部 \(x=\operatorname{Re} z\)、\(y\)軸を 虚部 \(y=\operatorname{Im} z\)にとった平面を 複素平面 と呼ぶ
共役複素数
複素数 \(z=x+i y\) に対して, \(\bar{z}=x-i y\) をその 共役(きょうやく)複素数 といい、 \(z, \bar{z}\) は 互いに複素共役である という。
これらは複素平面上で \(x\) 軸に関して対称な位置にある。
この定義から
\[
x=\frac{z+\bar{z}}{2}, \quad y=\frac{z-\bar{z}}{2 i}
\]
となる。また重要な関係として
\[
z \bar{z}=(x+i y)(x-i y)=x^2+y^2=|z|^2
\]
が成り立つ。
オイラーの式
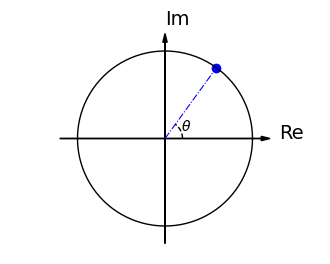
指数部が虚数の指数関数 \(e^{i \theta}\) を次の複素数と定義する。
\[
e^{i \theta}=\cos \theta+i \sin \theta
\]
これは オイラーの式 と呼ばれる式で、複素平面の単位円上の実軸から角度\(\theta\)の点を表す。
定理
\[
e^{i \theta} e^{i \phi}=e^{i(\theta+\phi)}
\]
が成り立つ。
定義より次のように変形できる
\[\begin{split}
\begin{aligned}
e^{i \theta} e^{i \phi} & =(\cos \theta+i \sin \theta)(\cos \phi+i \sin \phi) \\
& =(\cos \theta \cos \phi-\sin \theta \sin \phi)+i(\cos \theta \sin \phi+\sin \theta \cos \phi)\\
e^{i(\theta+\phi)} &=\cos (\theta+\phi)+i \sin (\theta+\phi)\\
\end{aligned}
\end{split}\]
両者が等しいことは、三角関数の加法定理
\[\begin{split}
\begin{aligned}
\cos (\theta+\phi) &=\cos \theta \cos \phi-\sin \theta \sin \phi\\
\sin (\theta+\phi) &=\cos \theta \sin \phi+\sin \theta \cos \phi
\end{aligned}
\end{split}\]
よりわかる
定理
\[
\cos \theta=\frac{e^{i \theta}+e^{-i \theta}}{2}
, \quad
\sin \theta=\frac{e^{i \theta}-e^{-i \theta}}{2 i}
\]
が成り立つ。
オイラーの式 およびその式の \(\theta\) を \(-\theta\) に置き換えた式
\[
e^{i \theta}=\cos \theta+i \sin \theta
, \quad
e^{-i \theta}=\cos \theta-i \sin \theta
\]
を使うと、
\[
e^{i \theta} + e^{-i \theta}
= \cos \theta + i \sin \theta + \cos \theta-i \sin \theta
= 2 \cos \theta
\]
より
\[
\cos \theta=\frac{e^{i \theta}+e^{-i \theta}}{2}
\]
が得られる。また
\[
e^{i \theta} - e^{-i \theta}
= \cos \theta + i \sin \theta - \cos \theta + i \sin \theta
= 2i \sin \theta
\]
より
\[
\sin \theta=\frac{e^{i \theta}-e^{-i \theta}}{2 i}
\]
が得られる。
フーリエ級数の複素表示
\[
\cos \theta=\frac{e^{i \theta}+e^{-i \theta}}{2}, \quad \sin \theta=\frac{e^{i \theta}-e^{-i \theta}}{2 i}
\]
を使うと、フーリエ級数は以下のように表すことができる。
\[\begin{split}
\begin{aligned}
f(t) & =\frac{a_0}{2}+\sum_{k=1}^{\infty}\left(a_k \frac{e^{i k \omega_o t}+e^{-i k \omega_o t}}{2}+b_k \frac{e^{i k \omega_o t}-e^{-i k \omega_o t}}{2 i}\right) \\
& =\frac{a_0}{2}+\frac{1}{2} \sum_{k=1}^{\infty}\left(\left(a_k-i b_k\right) e^{i k \omega_o t}+\left(a_k+i b_k\right) e^{-i k \omega_o t}\right)\\
& =\sum_{k=-\infty}^{\infty} C_k e^{i k \omega_o t}
\end{aligned}
\end{split}\]
ただし
\[\begin{split}
C_k=\left\{\begin{array}{cc}
\left(a_k-i b_k\right) / 2 & k>0 \\
a_0 / 2 & k=0 \\
\left(a_{-k}+i b_{-k}\right) / 2 & k<0
\end{array}\right.
\end{split}\]
である
また、\(C_k\)の各式は次のように変形できる
\[\begin{split}
\begin{aligned}
\frac{a_k-i b_k}{2} & =\frac{2}{T} \int_{-T / 2}^{T / 2} f(t) \frac{\cos k \omega_o t-i \sin k \omega_o t}{2} \mathrm{~d} t=\frac{1}{T} \int_{-T / 2}^{T / 2} f(t) e^{-i k \omega_o t} \mathrm{~d} t \\
\frac{a_0}{2} & =\frac{1}{T} \int_{-T / 2}^{T / 2} f(t) \mathrm{d} t \\
\frac{a_{-k}+i b_{-k}}{2} & =\frac{2}{T} \int_{-T / 2}^{T / 2} f(t) \frac{\cos \left(-k \omega_o t\right)+i \sin \left(-k \omega_o t\right)}{2} \mathrm{~d} t \\
& =\frac{1}{T} \int_{-T / 2}^{T / 2} f(t)\left(\cos k \omega_o t-i \sin k \omega_o t\right) \mathrm{d} t=\frac{1}{T} \int_{-T / 2}^{T / 2} f(t) e^{-i k \omega_o t} \mathrm{~d} t
\end{aligned}
\end{split}\]
\[
f(t)=\sum_{k=-\infty}^{\infty} C_k e^{i k \omega_o t}, \quad C_k=\frac{1}{T} \int_{-T / 2}^{T / 2} f(t) e^{-i k \omega_o t} \mathrm{~d} t
\]
この\(C_k\)を (複素)フーリエ係数 と呼ぶ。
フーリエ変換
フーリエ級数
\[
f(t)=\sum_{k=-\infty}^{\infty} C_k e^{i k \omega_o t}, \quad C_k=\frac{1}{T} \int_{-T / 2}^{T / 2} f(t) e^{-i k \omega_o t} \mathrm{~d} t
\]
において
\[
\omega_k=k \omega_o, \quad k=0, \pm 1, \pm 2, \ldots
\]
とおき、
\[
\Delta \omega=\omega_{k+1}-\omega_k=\omega_o=\frac{2 \pi}{T}, \quad C_k=\frac{F\left(\omega_k\right)}{T}
\]
と書くと、
\[
f(t)=\frac{1}{2 \pi} \sum_{k=-\infty}^{\infty} F\left(\omega_k\right) e^{i \omega_k t} \Delta \omega, \quad F\left(\omega_k\right)=\int_{-T / 2}^{T / 2} f(t) e^{-i \omega_k t} \mathrm{~d} t
\]
となる。周期\(T\to\infty\)とすると、\(\Delta \omega \to 0\)となり、積分として表すことができる。
\[
F(\omega)=\int_{-\infty}^{\infty} f(t) e^{-i \omega t} \mathrm{~d} t
\]
を信号\(f(t)\)の フーリエ変換 と呼び、
\[
f(t)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) e^{i \omega t} \mathrm{~d} \omega
\]
を 逆フーリエ変換 と呼ぶ。
フーリエ変換
\[
F(\omega)=\int_{-\infty}^{\infty} f(t) e^{-i \omega t} \mathrm{~d} t
\]
逆フーリエ変換
\[
f(t)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) e^{i \omega t} \mathrm{~d} \omega
\]
逆フーリエ変換は信号\(f(t)\)をあらゆる周波数(すべての実数の\(\omega\))の振動の重ね合わせで表す。
\(F(\omega)\)は周波数\(\omega\)の成分\(e^{i \omega t}\)の大きさを表し、\(f(t)\)の スペクトル (フランス語: spectre、英語: spectrum)と呼ばれる。(光をプリズムに通して各色のスペクトルに分けるイメージ)
\(|\omega|\)が大きい成分は 高周波成分 、小さい成分は 低周波成分 と呼ばれる。とくに\(\omega=0\)の成分は定数であり、 直流成分 と呼ばれる。
図:フーリエ変換のイメージ。\(F(\omega)\)は一般に複素数なのでグラフに書けない → 絶対値をとる
例:矩形窓
次の関数は幅\(W\)の 矩形窓(rectangular window) と呼ばれる
\[\begin{split}
w(t)=\left\{\begin{array}{cc}
1 / 2 W & -W \leq t \leq W \\
0 & \text { それ以外 }
\end{array}\right.
\end{split}\]
このフーリエ変換は
\[\begin{split}
\begin{aligned}
W(\omega)
&=\frac{1}{2 W} \int_{-W}^W e^{-i \omega t} \mathrm{~d} t \\
&=\frac{1}{2 W} \int_{-W}^W(\cos \omega t-i \sin \omega t) \mathrm{d} t \quad (オイラーの式より e^{-i \omega t} = \cos \omega t-i \sin \omega t)\\
&=\frac{1}{2 W} \left( \int_{-W}^W \cos \omega t ~\mathrm{d} t - \int_{-W}^W i \sin \omega t ~\mathrm{d} t \right)
\quad (\because 積分の線形性)
\\
&=\frac{1}{2W} \int_{-W}^W \cos \omega t ~ \mathrm{d} t
\quad (\because \sinは奇関数すなわち \sin(-\theta) = -\sin(\theta) であり、-Wから+Wまで積分したら0になるため消える )
\\
&=\frac{1}{W} \int_0^W \cos \omega t \mathrm{~d} t
\quad (\because \int_{-W}^W \cos \omega t ~ \mathrm{d} t = 2 \int_{0}^W \cos \omega t ~ \mathrm{d} t )
\\
&=\frac{1}{W}\left[ \frac{\sin \omega t}{\omega} \right]_0^W
\quad (\because \int \cos (\omega t) d t=\frac{\sin (\omega t)}{\omega} )
\\
&=\frac{1}{W} \left( \frac{\sin \omega W}{\omega} - \frac{\sin 0}{\omega} \right)
\\
&=\frac{\sin W \omega}{W \omega}
\quad (\because \sin 0 = 0)
\\
&=\operatorname{sinc} \frac{W}{\pi} \omega
\end{aligned}
\end{split}\]
となる。ただし、
\[
\operatorname{sinc} x :=\frac{\sin \pi x}{\pi x}
\]
と定義する。
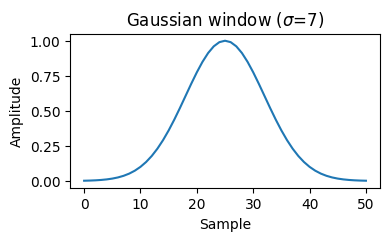
次の関数\(w(t)\) を幅\(\sigma\)の ガウス窓(Gaussian window) という。
\[
w(t)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-t^2 / 2 \sigma^2}
\]
このフーリエ変換は
\[\begin{split}
\begin{aligned}
W(\omega)
&= \int_{-\infty}^{\infty} w(t) e^{-i \omega t} \mathrm{~d} t \\
&= \frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^{\infty} e^{-t^2 / 2 \sigma^2} e^{-i \omega t} \mathrm{~d} t \\
&= \frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^{\infty}
e^{-( \frac{t^2}{2 \sigma^2} + i \omega t)} \mathrm{~d} t
\quad ( 指数法則 a^{n}a^m=a^{n+m})\\
&= \frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^{\infty} e^{-\left(t+i \sigma^2 \omega\right)^2 / 2 \sigma^2-\sigma^2 \omega^2 / 2} \mathrm{~d} t
\quad (平方完成したり色々いじるとこうなる)
\\
&= \left(\frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^{\infty} e^{-\left(t+i \sigma^2 \omega\right)^2 / 2 \sigma^2} \mathrm{~d} t\right) e^{-\sigma^2 \omega^2 / 2}
\end{aligned}
\end{split}\]
ここで \(z=t+i \sigma^2 \omega\)と変数変換すると
\[\begin{split}
\begin{aligned}
W(\omega)
& =\left(\frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^{\infty} e^{-z^2 / 2 \sigma^2} \mathrm{~d} z\right) e^{-\sigma^2 \omega^2 / 2} \\
& =e^{-\sigma^2 \omega^2 / 2}\\
&=\frac{\sqrt{2 \pi}}{\sigma}\left(\frac{1}{\sqrt{2 \pi} \sigma^{-1}} e^{-\omega^2 / 2 \sigma^{-2}}\right)
\end{aligned}
\end{split}\]
となる
(出典:gaussian — SciPy v1.14.1 Manual )
畳み込み積分
たたみこみ積分
次の積分を信号 \(f(t), g(t)\) の たたみこみ積分 (convolution) または 合成積 と呼ぶ
\[
f(t) * g(t)=\int_{-\infty}^{\infty} f(s) g(t-s) \mathrm{d} s
\]
(左辺の積分における\(f\)と\(g\)の変数の和が\(s + t-s = t\)となっている)
畳み込み積分は分配法則、交換法則、結合法則が成り立つ
分配法則: \(f(t) *(a g(t)+b h(t))=a f(t) * g(t)+b f(t) * h(t)\)
交換法則:\(f(t) * g(t)=g(t) * f(t)\)
結合法則:\((f(t) * g(t)) * h(t)=f(t) *(g(t) * h(t))\)
定理(信号の合成積はフーリエ変換の積)
信号 \(f(t), g(t)\) のフーリエ変換をそれぞれ \(F(\omega), G(\omega)\) とするとき、 \(f(t) * g(t)\) のフーリエ変換は \(F(\omega) G(\omega)\) である
\(f(t) * g(t)\)のフーリエ変換は次のようになる
\[\begin{split}
\begin{aligned}
\int_{-\infty}^{\infty} f(t) * g(t) e^{-i \omega t} \mathrm{~d} t & =\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty} f(s) g(t-s) \mathrm{d} s\right) e^{-i \omega t} \mathrm{~d} t \\
& =\int_{-\infty}^{\infty} f(s)\left(\int_{-\infty}^{\infty} g(t-s) e^{-i \omega t} \mathrm{~d} t\right) \mathrm{d} s \\
& =\int_{-\infty}^{\infty} f(s)\left(\int_{-\infty}^{\infty} g\left(t^{\prime}\right) e^{-i \omega\left(t^{\prime}+s\right)} \mathrm{d} t^{\prime}\right) \mathrm{d} s \\
& =\int_{-\infty}^{\infty} f(s)\left(\int_{-\infty}^{\infty} g\left(t^{\prime}\right) e^{-i \omega t^{\prime}} \mathrm{d} t^{\prime}\right) e^{-i \omega s} \mathrm{~d} s \\
& =\left(\int_{-\infty}^{\infty} f(s) e^{-i \omega s} \mathrm{~d} s\right)\left(\int_{-\infty}^{\infty} g\left(t^{\prime}\right) e^{-i \omega t^{\prime}} \mathrm{d} t^{\prime}\right) \\
& =F(\omega) G(\omega)
\end{aligned}
\end{split}\]
(積分の順序を入れ換え、 \(t^{\prime}=t-s\) と変数変換し、 \(t=t^{\prime}+s\) を代入した)
一般に、ある集合に要素間の演算が定義されているものを 代数系 と呼ぶ。そして2つの異なる集合での演算が同じ規則に従うとき、2つの代数系は 同型 であるという。
関数の和\(+\)と畳み込み積分\(*\)に関する演算は、そのフーリエ変換の和\(+\)と積\(\times\)に関する演算と同じであり、両方の代数系が同型である。
フィルター
信号 \(f(t)\) の値を時刻 \(t\) をはさむ幅 \(2 W\) の区間で平均し、これを \(\tilde{f}(t)\) と定義する。
\[
\tilde{f}(t) := \frac{1}{2 W} \int_{-W}^W f(t-s) \mathrm{d} s
\]
矩形窓やガウス窓\(w(t)\)を使うと、次のように書き直すことができる
\[
\tilde{f}(t)=\int_{-\infty}^{\infty} w(s) f(t-s) \mathrm{d} s=w(t) * f(t)
\]
これにより、関数\(w(t)\)を様々な関数に変えれば信号\(f(t)\)の様々な変換ができる。このような操作を関数\(w(t)\)による フィルター という。
\(w(t), f(t)\)のフーリエ変換をそれぞれ\(W(\omega), F(\omega)\)とおけば、畳み込み積分の定理により\(\tilde{f}(t) = w(t)*f(t)\)のフーリエ変換は
\[
\tilde{F}(\omega) = W(\omega) F(\omega)
\]
と書くことができる。
もし\(|\omega|\)が小さい部分で\(|W(\omega)|\)が大きく、\(|\omega|\)が大きい部分で\(|W(\omega)|\)が小さくなる場合、\(w(t)\)によるフィルターは低周波成分を増幅し、高周波成分を減衰させる。このようなフィルターを ローパスフィルター ( 低域フィルター )と呼ぶ。その逆のフィルターを ハイパスフィルター ( 高域フィルター )と呼ぶ。
その中間として、特定の\(|\omega|\)の付近を増幅し、それ以外を減衰させるフィルターは 帯域フィルター ( バンドパスフィルター )と呼ぶ。
小まとめ
信号\(f(t)\)をフーリエ変換
\[
F(\omega)=\int_{-\infty}^{\infty} f(t) e^{-i \omega t} \mathrm{~d} t
\]
して、個々の\(\omega\)に対応するスペクトル(周波数\(\omega\)の影響度の強さ)\(F(\omega)\)を得ることができ、またそれにより\(f(t)\)に含まれる周波数ごとの正弦波\(e^{i\omega t}\)も分解できる。
そして窓関数\(w(t)\)による畳み込み
\[
\tilde{f}(t) = w(t) * f(t) = \int_{-\infty}^{\infty} w(s) f(t-s) \mathrm{d} s
\]
をすることで、特定の周波数をカットするなどの変換を行って信号を変換することができる。
一つの身近な具体例は画像に対するガウシアンフィルタ(ガウシアン平滑化・ガウシアンブラー)によるぼかし
パワースペクトル
パーセバル(・プランシュレル)の式
信号 \(f(t), g(t)\) のフーリエ変換をそれぞれ \(F(\omega), G(\omega)\) とする。
このとき、以下の パーセバル(・プランシュレル)の式 が成り立つ
\[\begin{split}
\int_{-\infty}^{\infty} f(t) \overline{g(t)} ~\mathrm{d} t
=\frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) \overline{G(\omega)} ~\mathrm{d} \omega
\\
\int_{-\infty}^{\infty}|f(t)|^2 \mathrm{~d} t
=\frac{1}{2 \pi} \int_{-\infty}^{\infty}|F(\omega)|^2 \mathrm{~d} \omega
\end{split}\]
\[
\int_{-\infty}^{\infty} f(t) \overline{g(t)} ~\mathrm{d} t
=\frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) \overline{G(\omega)} ~\mathrm{d} \omega
\]
については、
\[\begin{split}
\begin{aligned}
\int_{-\infty}^{\infty} f(t) \overline{g(t)} \mathrm{d} t
& =\int_{-\infty}^{\infty} f(t)\left(\frac{1}{2 \pi} \int_{-\infty}^{\infty} \overline{G(\omega)} e^{-i \omega t} \mathrm{~d} \omega\right) \mathrm{d} t \\
& =\frac{1}{2 \pi} \int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty} f(t) e^{-i \omega t} \mathrm{~d} t\right) \overline{G(\omega)} \mathrm{d} \omega \\
& =\frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) \overline{G(\omega)} \mathrm{d} \omega
\end{aligned}
\end{split}\]
\(g(t) = f(t)\)とすると
\[
\int_{-\infty}^{\infty}|f(t)|^2 \mathrm{~d} t
=\frac{1}{2 \pi} \int_{-\infty}^{\infty}|F(\omega)|^2 \mathrm{~d} \omega
\]
が得られる
信号\(f(t)\)が時間\(t\)とともに変動する振動を表すとき、\(|f(t)|^2\)はその振動の単位時間あたりの エネルギー とみなすことができる。
パーセバルの第2式
\[
\int_{-\infty}^{\infty}|f(t)|^2 \mathrm{~d} t
=\frac{1}{2 \pi} \int_{-\infty}^{\infty} |F(\omega)|^2 \mathrm{~d} \omega
\]
はエネルギーがすべての\(\omega\)にわたる\(|F(\omega)|^2\)の積分で表されることを意味する。
これを パワースペクトル と呼び、
\[
P(\omega) = |F(\omega)|^2
\]
は周波数\(\omega\)の振動成分のもつエネルギーであると解釈できる。
フーリエ変換\(F(\omega)\)は一般に複素数だが、その絶対値は実数になりグラフに描くことができる。
フーリエ変換は共役\(F(-\omega) = \overline{F(\omega)}\)であり\(|F(-\omega)| = |\overline{F(\omega)}|\)だから、パワースペクトルはグラフにすると原点を中心に左右対称になる。
複素計量空間(ユニタリ空間)とのつながり
信号\(f,g\)の内積を
\[
(f, g) := \int_{-\infty}^{\infty} f(t) \overline{g(t)} ~\mathrm{d} t
\]
と定義すれば、ノルムも
\[
\|f\| = \sqrt{(f,f)}
\]
と定義でき、フーリエ変換も
\[
(F, G):=\frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) \overline{G(\omega)} \mathrm{d} \omega
\]
とおけば
\[
\|F\|=\sqrt{\frac{1}{2 \pi} \int_{-\infty}^{\infty}|F(\omega)|^2 \mathrm{~d} \omega}
\]
となり、パーセバルの式は
\[
(f, g)=(F, G), \quad\|f\|^2=\|F\|^2
\]
とシンプルでエレガントな表記にすることができる。
この内積は計量ベクトル空間の内積の公理のうち対称性\((f,g) = (g,f)\)を満たさないが、ユニタリ空間におけるエルミート対称性\((f,g) = \overline{(g,f)}\)は満たす。つまり、ユニタリ空間上で考えるなら上のシンプルな表記が可能。
(エルミート)内積
スカラとして複素数を取る線形空間\(\mathcal{L}\)を 複素線形空間 といい、任意の元\(\boldsymbol{u},\boldsymbol{v} \in \mathcal{L}\)について次の性質を満たす複素数\((\boldsymbol{u},\boldsymbol{v})\)が定義されるとき、それを (エルミート)内積 という。
任意の \(\boldsymbol{u} \in \mathcal{L}\) に対して \((\boldsymbol{u}, \boldsymbol{u}) \geq 0\). 等号が成り立つのは \(\boldsymbol{u}=\mathbf{0}\) のときのみ ( 正値性 )
任意の \(\boldsymbol{u}, \boldsymbol{v} \in \mathcal{L}\) に対して \((\boldsymbol{u}, \boldsymbol{v})=\overline{(\boldsymbol{v}, \boldsymbol{u})}\) ( エルミート対称性 )
任意の複素数 \(c_1, c_2\) と任意の \(\boldsymbol{u}, \boldsymbol{v}_1, \boldsymbol{v}_2 \in \mathcal{L}\) に対して \(\left(c_1 \boldsymbol{u}_1+c_2 \boldsymbol{u}_2, \boldsymbol{v}\right)=c_1\left(\boldsymbol{u}_1, \boldsymbol{v}\right)+\) \(c_2\left(u_2, \boldsymbol{v}\right)\) ( 線形性 )
(ユニタリ)ノルム
\(\mathcal{L}\) を複素線形空間とする。 \(\boldsymbol{u} \in \mathcal{L}\) の (ユニタリ)ノルム を次のように定義する
\[
\|\boldsymbol{u}\| = \sqrt{(\boldsymbol{u},\boldsymbol{u})}
\]
ユニタリ空間(複素計量空間)
上記のような内積とノルムが定義されている複素線形空間\(\mathcal{L}\)を ユニタリ空間 または 複素計量空間 という。
自己相関関数
自己相関関数
次の関数 \(R(\tau)\) を信号 \(f(t)\) の 自己相関関数 と呼ぶ。
\[
R(\tau)=\int_{-\infty}^{\infty} f(t) \overline{f(t-\tau)} ~\mathrm{d} t
\]
\(R(0)\) は信号 \(f(t)\) のエネルギー \(\int_{-\infty}^{\infty}|f(t)|^2 \mathrm{~d} t\) に等しく、通常は大きな値をとる。
\(|\tau|\) が大きくなると \(R(\tau)\) は急速に減衰する。
なぜ自己相関関数と呼ぶのか
実数の信号 \(f(t), g(t)\) の内積 \(\int_{-\infty}^{\infty} f(t) g(t) \mathrm{d} t\) の場合、\(f(t)\)と\(g(t)\)が無関係なら\(f(t)g(t)\)はそれぞれプラスとマイナスで打ち消し合ったりして小さい値になるが、\(f(t)\)と\(g(t)\)が似てるなら\(f(t)g(t)\approx f(t)^2 \geq 0\)となり、積分すると大きな値になる。
複素数の信号の場合はエルミート内積\(\int_{-\infty}^{\infty} f(t) \overline{g(t)} \mathrm{d} t\)を考えると、もし\(f(t)\)と\(g(t)\)が似てるなら\(f(t)g(t) \approx f(t)\overline{f(t)} \approx |f(t)|^2 \geq 0\)となり、積分すると大きな値になる。
このように、内積・エルミート内積は類似度の尺度となり、 (相互)相関 と呼ばれる。
\(f(t)\) と、それを\(\tau\)だけ平行移動した \(f(t-\tau)\) の類似度なので自己相関と呼ばれる。
自己相関関数の性質
\[
R(-\tau)=\overline{R(\tau)}
, \quad|R(-\tau)|=|R(\tau)|
\]
第1式は
\[\begin{split}
\begin{aligned}
R(-\tau) &=\int_{-\infty}^{\infty} f(t) \overline{f(t+\tau)} \mathrm{d} t\\
&=\int_{-\infty}^{\infty} f\left(t^{\prime}-\tau\right) \overline{f\left(t^{\prime}\right)} \mathrm{d} t^{\prime} \\
&=\overline{\int_{-\infty}^{\infty} f\left(t^{\prime}\right) \overline{f\left(t^{\prime}-\tau\right)} \mathrm{d} t^{\prime}}=\overline{R(\tau)}
\end{aligned}
\end{split}\]
で示される。また共役複素数をとっても絶対値は変化しないため第2式が成り立つ。
ウィーナー・ヒンチンの定理
ウィーナー・ヒンチンの定理
自己相関関数のフーリエ変換はパワースペクトルに等しい。
\[
P(\omega)=\int_{-\infty}^{\infty} R(\tau) e^{-i \omega \tau} \mathrm{~d} \tau
\]
よってパワースペクトルを算出するには、2通りの方法がある
信号\(f(t)\)のフーリエ変換\(F(\omega)\)を計算して絶対値の2乗を取る
自己相関関数\(R(\tau)\)を計算してフーリエ変換する
信号を精度よく積分するのは難しいため、自己相関関数で算出するほうが実用上は便利らしい
それっぽいやつやってみたがうまくPが一致しない
そもそもホワイトノイズのPは1のはず…
サンプリング定理
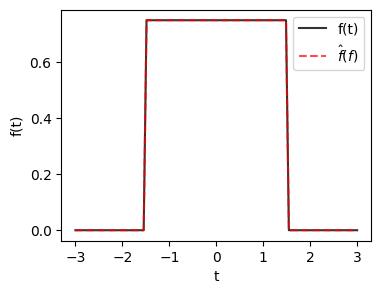
信号 \(f(t)\) の離散的な点 \(\left\{t_k\right\}, k=0, \pm 1, \pm 2, \pm 3, \ldots\) での値 \(\left\{f_k\right\}\) を サンプル点 \(\left\{t_k\right\}\) での サンプル値 と呼ぶ。
サンプル点 \(\left\{t_k\right\}\) の間隔 \(\tau\) を サンプル間隔 と呼ぶ。サンプル値 \(\left\{f_k\right\}\) のみから連続関数を再現することを 補間 という。
次の性質を持つ関数 \(\phi(t)\) をサンプル間隔 \(\tau\) の 補間関数 と呼ぶ
\[\begin{split}
\phi(t)= \begin{cases}1 & t=0 \\ 0 & t= \pm \tau, \pm 2 \tau, \pm 3 \tau, \ldots\end{cases}
\end{split}\]
補間関数の例は\(\operatorname{sinc}\)(cardinal sine)関数
\[
\operatorname{sinc}(x) =\frac{\sin \pi x}{\pi x}
\]
\[
\hat{f}(t)=\sum_{k=-\infty}^{\infty} f_k \phi\left(t-t_k\right)
\]
はすべてのサンプル点\(t_i\)でサンプルの値\(f_i\)をとる
定義:帯域制限
信号\(f(t)\)のフーリエ変換を\(F(\omega)\)とするとき、
\[
|\omega| \geq W \implies F(\omega)=0
\]
であれば、信号\(f(t)\)は 帯域幅 \(W\) に 帯域制限 されているという
サンプリング間隔\(\tau\)を半周期(波1つ分。sinなら\(\pi\)の幅)とする振動は各周波数\(W=\pi/\tau\)を持つ
サンプリング定理
帯域幅 \(W\) に帯域制限された信号 \(f(t)\) はサンプル間隔
\[
\tau=\frac{\pi}{W}
\]
のサンプル点 \(\left\{t_k\right\}\) でのサンプル値 \(\left\{f_k\right\}\) のみから次のように再現される
\[
f(t)=\sum_{k=-\infty}^{\infty} f_k \operatorname{sinc} \frac{t-t_k}{\tau}
\]
信号\(f(t)\)のフーリエ変換は
\[
f(t)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) e^{i \omega t} \mathrm{~d} \omega, \quad F(\omega)=\int_{-\infty}^{\infty} f(t) e^{-i \omega t} \mathrm{~d} t
\]
となる。\(F(\omega)\)は区間\([-W,W]\)でフーリエ級数に展開できる
\[
F(\omega)=\sum_{k=-\infty}^{\infty} C_k e^{i \pi k \omega / W}, \quad C_k=\frac{1}{2 W} \int_{-W}^W F(\omega) e^{-i \pi k \omega / W} \mathrm{~d} \omega
\]
区間 \([-W, W]\) の外では \(F(\omega)=0\) であるから、 \(C_k\) は次のように計算できる。
\[\begin{split}
\begin{aligned}
C_k & =\frac{1}{2 W} \int_{-\infty}^{\infty} F(\omega) e^{-i \pi k \omega / W} \mathrm{~d} \omega\\
&=\frac{\pi}{W} \frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) e^{i \omega(-\pi k / W)} \mathrm{d} \omega \\
& =\frac{\pi}{W} f\left(-\frac{\pi k}{W}\right)=\tau f(-k \tau)=\tau f_{-k}
\end{aligned}
\end{split}\]
よって\(F(\omega)\)は区間\([-W,W]\)で
\[\begin{split}
\begin{aligned}
F(\omega) & =\sum_{k=-\infty}^{\infty} \tau f_{-k} e^{i \pi k \omega / W}=\tau \sum_{k=-\infty}^{\infty} f_k e^{-i \pi k \omega / W} \\
& =\tau \sum_{k=-\infty}^{\infty} f_k e^{-i k \tau \omega}=\tau \sum_{k=-\infty}^{\infty} f_k e^{-i t_k \omega}
\end{aligned}
\end{split}\]
となる。
まとめると、
\[\begin{split}
\begin{aligned}
f(t) & =\frac{1}{2 \pi} \int_{-W}^W F(\omega) e^{i \omega t} \mathrm{~d} \omega\\
& =\frac{1}{2 \pi} \int_{-W}^W\left(\tau \sum_{k=-\infty}^{\infty} f_k e^{-i t_k \omega}\right) e^{i \omega t} \mathrm{~d} \omega \\
& =\frac{\tau}{2 \pi} \sum_{k=-\infty}^{\infty} f_k \int_{-W}^W e^{i\left(t-t_k\right) \omega} \mathrm{d} \omega \\
& =\frac{\tau}{2 \pi} \sum_{k=-\infty}^{\infty} f_k \int_{-W}^W\left(\cos \left(t-t_k\right) \omega+i \sin \left(t-t_k\right) \omega\right) \mathrm{d} \omega \\
& =\frac{\tau}{\pi} \sum_{k=-\infty}^{\infty} f_k \int_0^W \cos \left(t-t_k\right) \omega \mathrm{d} \omega \\
& =\frac{1}{W} \sum_{k=-\infty}^{\infty} f_k \int_0^W \cos \left(t-t_k\right) \omega \mathrm{d} \omega
\quad (\because \tau = \pi/W) \\
& =\frac{1}{W} \sum_{k=-\infty}^{\infty} f_k\left[\frac{\sin \left(t-t_k\right) \omega}{\left(t-t_k\right)}\right]_0^W\\
& =\sum_{k=-\infty}^{\infty} f_k \frac{\sin W\left(t-t_k\right)}{W\left(t-t_k\right)} \\
& =\sum_{k=-\infty}^{\infty} f_k \operatorname{sinc} \frac{W\left(t-t_k\right)}{\pi}\\
& =\sum_{k=-\infty}^{\infty} f_k \operatorname{sinc} \frac{t-t_k}{\tau}
\end{aligned}
\end{split}\]
一定の条件を満たす間隔で得られたサンプルと、一定の条件を満たす信号は、 離散的なサンプルからもとの連続的な信号を再現できる というのがサンプリング定理。
音声などの信号に限らず、デジタル画像などアナログ(連続値)なものをデジタル(離散値)にサンプリングする分野で広く応用されている。
間隔\(\tau\)でサンプリングすると\(W=\pi/\tau\)以上の周波数の信号は捉えられない。\(W=\pi/\tau\)をサンプリング間隔\(\tau\)に対する ナイキスト周波数 とよぶ。
周期\(T\)が\(T=2\tau\)なら、周波数が\(\omega=2\pi/T=\pi/\tau=W\)
1周期が\(T = 2\tau = 2\pi\)のsinに対してサンプリング間隔が\(\tau = \pi\)だとナイキスト周波数であり、もとの信号が復元できない様子。\(\omega = 2\pi/T = 2\pi/2\pi = 1\)…?