DoubleMLパッケージによるDMLのシミュレーション#
参考：Python: Basics of Double Machine Learning — DoubleML documentation
import warnings
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
from lightgbm import LGBMRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.base import clone
from doubleml import DoubleMLData
from doubleml import DoubleMLPLR
from doubleml.datasets import make_plr_CCDDHNR2018
face_colors = sns.color_palette('pastel')
edge_colors = sns.color_palette('dark')
warnings.filterwarnings("ignore")
np.random.seed(1234)
n_rep = 1000
n_obs = 500
n_vars = 5
alpha = 0.5
data = list()
for i_rep in range(n_rep):
(x, y, d) = make_plr_CCDDHNR2018(alpha=alpha, n_obs=n_obs, dim_x=n_vars, return_type='array')
data.append((x, y, d))
naiive estimator#
\[
\hat{\theta}_0 = \left(\frac{1}{n} \sum_{i\in I} D_i^2\right)^{-1} \frac{1}{n} \sum_{i\in I} D_i (Y_i - \hat{g}_0(X_i)).
\]
def non_orth_score(y, d, l_hat, m_hat, g_hat, smpls):
u_hat = y - g_hat
psi_a = -np.multiply(d, d)
psi_b = np.multiply(d, u_hat)
return psi_a, psi_b
なお、\(\hat{g}_0(X)\)は直接推定できないため間接的に推定している
np.random.seed(1111)
ml_l = LGBMRegressor(n_estimators=300, learning_rate=0.1)
ml_m = LGBMRegressor(n_estimators=300, learning_rate=0.1)
ml_l = RandomForestRegressor(n_estimators=100, max_features=10, max_depth=5, min_samples_leaf=5)
ml_m = RandomForestRegressor(n_estimators=200, max_features=10, max_depth=5, min_samples_leaf=5)
ml_g = clone(ml_l)
theta_nonorth = np.full(n_rep, np.nan)
se_nonorth = np.full(n_rep, np.nan)
for i_rep in range(n_rep):
print(f'Replication {i_rep+1}/{n_rep}', end='\r')
(x, y, d) = data[i_rep]
# choose a random sample for training and estimation
i_train, i_est = train_test_split(np.arange(n_obs), test_size=0.5, random_state=42)
# fit the ML algorithms on the training sample
ml_l.fit(x[i_train, :], y[i_train])
ml_m.fit(x[i_train, :], d[i_train])
psi_a = -np.multiply(d[i_train] - ml_m.predict(x[i_train, :]), d[i_train] - ml_m.predict(x[i_train, :]))
psi_b = np.multiply(d[i_train] - ml_m.predict(x[i_train, :]), y[i_train] - ml_l.predict(x[i_train, :]))
theta_initial = -np.nanmean(psi_b) / np.nanmean(psi_a)
ml_g.fit(x[i_train, :], y[i_train] - theta_initial * d[i_train])
# create out-of-sample predictions
l_hat = ml_l.predict(x[i_est, :])
m_hat = ml_m.predict(x[i_est, :])
g_hat = ml_g.predict(x[i_est, :])
external_predictions = {
'd': {
'ml_l': l_hat.reshape(-1, 1),
'ml_m': m_hat.reshape(-1, 1),
'ml_g': g_hat.reshape(-1, 1)
}
}
obj_dml_data = DoubleMLData.from_arrays(x[i_est, :], y[i_est], d[i_est])
obj_dml_plr_nonorth = DoubleMLPLR(obj_dml_data,
ml_l, ml_m, ml_g,
n_folds=2,
score=non_orth_score)
obj_dml_plr_nonorth.fit(external_predictions=external_predictions)
theta_nonorth[i_rep] = obj_dml_plr_nonorth.coef[0]
se_nonorth[i_rep] = obj_dml_plr_nonorth.se[0]
fig_non_orth, ax = plt.subplots(constrained_layout=True);
ax = sns.histplot((theta_nonorth - alpha)/se_nonorth,
color=face_colors[0], edgecolor = edge_colors[0],
stat='density', bins=30, label='Non-orthogonal ML');
ax.axvline(0., color='k');
xx = np.arange(-5, +5, 0.001)
yy = stats.norm.pdf(xx)
ax.plot(xx, yy, color='k', label='$\\mathcal{N}(0, 1)$');
ax.legend(loc='upper right', bbox_to_anchor=(1.2, 1.0));
ax.set_xlim([-6., 6.]);
ax.set_xlabel('$(\hat{\\theta}_0 - \\theta_0)/\hat{\sigma}$');
plt.show()
Replication 1/1000
Replication 2/1000
Replication 3/1000
Replication 4/1000
Replication 5/1000
Replication 6/1000
Replication 7/1000
Replication 8/1000
Replication 9/1000
Replication 10/1000
Replication 11/1000
Replication 12/1000
Replication 13/1000
Replication 14/1000
Replication 15/1000
Replication 16/1000
Replication 17/1000
Replication 18/1000
Replication 19/1000
Replication 20/1000
Replication 21/1000
Replication 22/1000
Replication 23/1000
Replication 24/1000
Replication 25/1000
Replication 26/1000
Replication 27/1000
Replication 28/1000
Replication 29/1000
Replication 30/1000
Replication 31/1000
Replication 32/1000
Replication 33/1000
Replication 34/1000
Replication 35/1000
Replication 36/1000
Replication 37/1000
Replication 38/1000
Replication 39/1000
Replication 40/1000
Replication 41/1000
Replication 42/1000
Replication 43/1000
Replication 44/1000
Replication 45/1000
Replication 46/1000
Replication 47/1000
Replication 48/1000
Replication 49/1000
Replication 50/1000
Replication 51/1000
Replication 52/1000
Replication 53/1000
Replication 54/1000
Replication 55/1000
Replication 56/1000
Replication 57/1000
Replication 58/1000
Replication 59/1000
Replication 60/1000
Replication 61/1000
Replication 62/1000
Replication 63/1000
Replication 64/1000
Replication 65/1000
Replication 66/1000
Replication 67/1000
Replication 68/1000
Replication 69/1000
Replication 70/1000
Replication 71/1000
Replication 72/1000
Replication 73/1000
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
Cell In[3], line 27
25 psi_b = np.multiply(d[i_train] - ml_m.predict(x[i_train, :]), y[i_train] - ml_l.predict(x[i_train, :]))
26 theta_initial = -np.nanmean(psi_b) / np.nanmean(psi_a)
---> 27 ml_g.fit(x[i_train, :], y[i_train] - theta_initial * d[i_train])
29 # create out-of-sample predictions
30 l_hat = ml_l.predict(x[i_est, :])
File /usr/local/lib/python3.10/site-packages/sklearn/base.py:1473, in _fit_context.<locals>.decorator.<locals>.wrapper(estimator, *args, **kwargs)
1466 estimator._validate_params()
1468 with config_context(
1469 skip_parameter_validation=(
1470 prefer_skip_nested_validation or global_skip_validation
1471 )
1472 ):
-> 1473 return fit_method(estimator, *args, **kwargs)
File /usr/local/lib/python3.10/site-packages/sklearn/ensemble/_forest.py:489, in BaseForest.fit(self, X, y, sample_weight)
478 trees = [
479 self._make_estimator(append=False, random_state=random_state)
480 for i in range(n_more_estimators)
481 ]
483 # Parallel loop: we prefer the threading backend as the Cython code
484 # for fitting the trees is internally releasing the Python GIL
485 # making threading more efficient than multiprocessing in
486 # that case. However, for joblib 0.12+ we respect any
487 # parallel_backend contexts set at a higher level,
488 # since correctness does not rely on using threads.
--> 489 trees = Parallel(
490 n_jobs=self.n_jobs,
491 verbose=self.verbose,
492 prefer="threads",
493 )(
494 delayed(_parallel_build_trees)(
495 t,
496 self.bootstrap,
497 X,
498 y,
499 sample_weight,
500 i,
501 len(trees),
502 verbose=self.verbose,
503 class_weight=self.class_weight,
504 n_samples_bootstrap=n_samples_bootstrap,
505 missing_values_in_feature_mask=missing_values_in_feature_mask,
506 )
507 for i, t in enumerate(trees)
508 )
510 # Collect newly grown trees
511 self.estimators_.extend(trees)
File /usr/local/lib/python3.10/site-packages/sklearn/utils/parallel.py:74, in Parallel.__call__(self, iterable)
69 config = get_config()
70 iterable_with_config = (
71 (_with_config(delayed_func, config), args, kwargs)
72 for delayed_func, args, kwargs in iterable
73 )
---> 74 return super().__call__(iterable_with_config)
File /usr/local/lib/python3.10/site-packages/joblib/parallel.py:1918, in Parallel.__call__(self, iterable)
1916 output = self._get_sequential_output(iterable)
1917 next(output)
-> 1918 return output if self.return_generator else list(output)
1920 # Let's create an ID that uniquely identifies the current call. If the
1921 # call is interrupted early and that the same instance is immediately
1922 # re-used, this id will be used to prevent workers that were
1923 # concurrently finalizing a task from the previous call to run the
1924 # callback.
1925 with self._lock:
File /usr/local/lib/python3.10/site-packages/joblib/parallel.py:1847, in Parallel._get_sequential_output(self, iterable)
1845 self.n_dispatched_batches += 1
1846 self.n_dispatched_tasks += 1
-> 1847 res = func(*args, **kwargs)
1848 self.n_completed_tasks += 1
1849 self.print_progress()
File /usr/local/lib/python3.10/site-packages/sklearn/utils/parallel.py:136, in _FuncWrapper.__call__(self, *args, **kwargs)
134 config = {}
135 with config_context(**config):
--> 136 return self.function(*args, **kwargs)
File /usr/local/lib/python3.10/site-packages/sklearn/ensemble/_forest.py:192, in _parallel_build_trees(tree, bootstrap, X, y, sample_weight, tree_idx, n_trees, verbose, class_weight, n_samples_bootstrap, missing_values_in_feature_mask)
189 elif class_weight == "balanced_subsample":
190 curr_sample_weight *= compute_sample_weight("balanced", y, indices=indices)
--> 192 tree._fit(
193 X,
194 y,
195 sample_weight=curr_sample_weight,
196 check_input=False,
197 missing_values_in_feature_mask=missing_values_in_feature_mask,
198 )
199 else:
200 tree._fit(
201 X,
202 y,
(...)
205 missing_values_in_feature_mask=missing_values_in_feature_mask,
206 )
File /usr/local/lib/python3.10/site-packages/sklearn/tree/_classes.py:472, in BaseDecisionTree._fit(self, X, y, sample_weight, check_input, missing_values_in_feature_mask)
461 else:
462 builder = BestFirstTreeBuilder(
463 splitter,
464 min_samples_split,
(...)
469 self.min_impurity_decrease,
470 )
--> 472 builder.build(self.tree_, X, y, sample_weight, missing_values_in_feature_mask)
474 if self.n_outputs_ == 1 and is_classifier(self):
475 self.n_classes_ = self.n_classes_[0]
KeyboardInterrupt:
Overcoming regularization bias by orthogonalization#
orthogonalized regressor \(V=D-m(X)\)を用いる推定量
\[
\check{\theta}_0 = \left(\frac{1}{n} \sum_{i\in I} \hat{V}_i D_i\right)^{-1} \frac{1}{n} \sum_{i\in I} \hat{V}_i (Y_i - \hat{g}_0(X_i)).
\]
np.random.seed(2222)
theta_orth_nosplit = np.full(n_rep, np.nan)
se_orth_nosplit = np.full(n_rep, np.nan)
for i_rep in range(n_rep):
print(f'Replication {i_rep+1}/{n_rep}', end='\r')
(x, y, d) = data[i_rep]
# fit the ML algorithms on the training sample
ml_l.fit(x, y)
ml_m.fit(x, d)
psi_a = -np.multiply(d - ml_m.predict(x), d - ml_m.predict(x))
psi_b = np.multiply(d - ml_m.predict(x), y - ml_l.predict(x))
theta_initial = -np.nanmean(psi_b) / np.nanmean(psi_a)
ml_g.fit(x, y - theta_initial * d)
l_hat = ml_l.predict(x)
m_hat = ml_m.predict(x)
g_hat = ml_g.predict(x)
external_predictions = {
'd': {
'ml_l': l_hat.reshape(-1, 1),
'ml_m': m_hat.reshape(-1, 1),
'ml_g': g_hat.reshape(-1, 1)
}
}
obj_dml_data = DoubleMLData.from_arrays(x, y, d)
obj_dml_plr_orth_nosplit = DoubleMLPLR(obj_dml_data,
ml_l, ml_m, ml_g,
score='IV-type')
obj_dml_plr_orth_nosplit.fit(external_predictions=external_predictions)
theta_orth_nosplit[i_rep] = obj_dml_plr_orth_nosplit.coef[0]
se_orth_nosplit[i_rep] = obj_dml_plr_orth_nosplit.se[0]
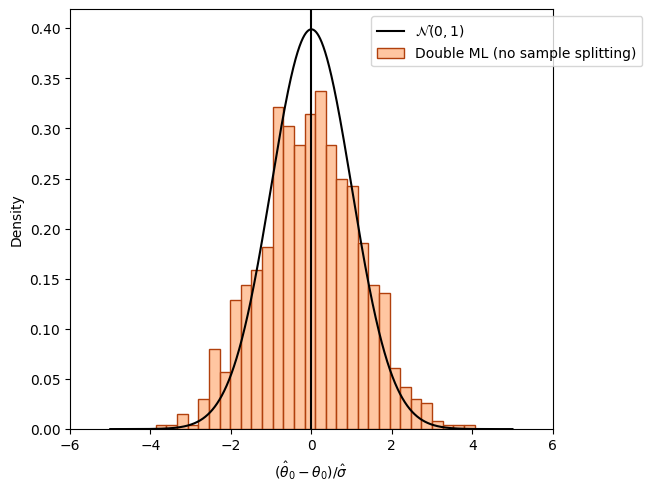
fig_orth_nosplit, ax = plt.subplots(constrained_layout=True);
ax = sns.histplot((theta_orth_nosplit - alpha)/se_orth_nosplit,
color=face_colors[1], edgecolor = edge_colors[1],
stat='density', bins=30, label='Double ML (no sample splitting)');
ax.axvline(0., color='k');
xx = np.arange(-5, +5, 0.001)
yy = stats.norm.pdf(xx)
ax.plot(xx, yy, color='k', label='$\\mathcal{N}(0, 1)$');
ax.legend(loc='upper right', bbox_to_anchor=(1.2, 1.0));
ax.set_xlim([-6., 6.]);
ax.set_xlabel('$(\hat{\\theta}_0 - \\theta_0)/\hat{\sigma}$');
plt.show()
Replication 1000/1000
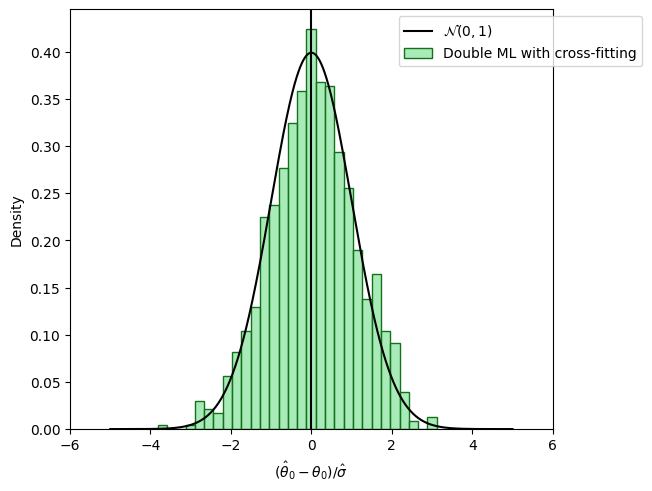
Sample splitting to remove bias induced by overfitting#
np.random.seed(3333)
theta_dml = np.full(n_rep, np.nan)
se_dml = np.full(n_rep, np.nan)
for i_rep in range(n_rep):
print(f'Replication {i_rep+1}/{n_rep}', end='\r')
(x, y, d) = data[i_rep]
obj_dml_data = DoubleMLData.from_arrays(x, y, d)
obj_dml_plr = DoubleMLPLR(obj_dml_data,
ml_l, ml_m, ml_g,
n_folds=2,
score='IV-type')
obj_dml_plr.fit()
theta_dml[i_rep] = obj_dml_plr.coef[0]
se_dml[i_rep] = obj_dml_plr.se[0]
fig_dml, ax = plt.subplots(constrained_layout=True);
ax = sns.histplot((theta_dml - alpha)/se_dml,
color=face_colors[2], edgecolor = edge_colors[2],
stat='density', bins=30, label='Double ML with cross-fitting');
ax.axvline(0., color='k');
xx = np.arange(-5, +5, 0.001)
yy = stats.norm.pdf(xx)
ax.plot(xx, yy, color='k', label='$\\mathcal{N}(0, 1)$');
ax.legend(loc='upper right', bbox_to_anchor=(1.2, 1.0));
ax.set_xlim([-6., 6.]);
ax.set_xlabel('$(\hat{\\theta}_0 - \\theta_0)/\hat{\sigma}$');
plt.show()
Replication 1000/1000
