相関係数

相関係数#

ピアソンの積率相関係数#

ピアソンの積率相関係数

r = \frac{Cov (X, Y)}{σ_{Y} σ_{Y}}

$Cov (X, Y)$ ：XとYの共分散
$σ_{Y}, σ_{Y}$ ：XとYの標準偏差

ピアソンの積率相関係数（標本レベル）

\hat{r} = \frac{\sum (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\sum {(x_{i} - \bar{x})}^{2}} \sqrt{\sum {(y_{i} - \bar{y})}^{2}}}

$\hat{r}$ ：相関係数。 $r \in [- 1, 1]$
$x_{i}$ ：標本における変数 $x$ の値
$\bar{x}$ ：変数 $x$ の値の平均
$y_{i}$ ：標本における変数 $y$ の値
$\bar{y}$ ：変数 $y$ の値の平均

どうやって $[- 1, 1]$ の範囲に収まるよう正規化しているのか？#

結論：コーシー・シュワルツの不等式を確率変数にあてはめている。

前提：内積#

ベクトル空間（要素間の和と定数倍が定義された集合であり、和と定数倍の結果もまた集合の要素であるような集合）における内積について触れておく。

（参考）内積の定義

$R$ 上のベクトル空間 $V$ において、任意の2つのベクトル $a, b$ に対して実数 $⟨ a, b ⟩$ が定まり、次の(1)～(4)を満たすとき、 $⟨ a, b ⟩$ を $a$ と $b$ の内積という。

(1) $⟨ a, b ⟩ = ⟨ b, a ⟩$

(2) $⟨ a + b, c ⟩ = ⟨ a, c ⟩ + ⟨ b, c ⟩$

(3) $⟨ k a, b ⟩ = k ⟨ a, b ⟩ (k \in R)$

(4) $⟨ a, a ⟩ ≧ 0$ で， $⟨ a, a ⟩ = 0 ⟺ a = 0$

また、内積 $⟨ a, b ⟩$ とノルム $‖ a ‖ = \sqrt{⟨ a, a ⟩}$ についての定理のひとつで コーシー・シュワルツの不等式

\begin{array}{r} \begin{aligned} | ⟨ a, b ⟩ | \leq ‖ a ‖ \cdot ‖ b ‖ \\ ⟺ & - ‖ a ‖ \cdot ‖ b ‖ \leq ⟨ a, b ⟩ \leq ‖ a ‖ \cdot ‖ b ‖ \\ ⟺ & - 1 \leq \frac{⟨ a, b ⟩}{‖ a ‖ \cdot ‖ b ‖} \leq 1 \end{aligned} \end{array}

というものが存在する。

なお、 $\frac{⟨ a, b ⟩}{‖ a ‖ \cdot ‖ b ‖}$ は コサイン類似度 と呼ばれ、ベクトル間の類似性を示すのでデータサイエンスの世界でよく使われる。

具体的な内積の例#

実数空間 $R$ 上のベクトル空間における内積の定義を満たす関数の例は次の通り。 $x, y \in R^{n}$ に対し、

⟨ x, y ⟩ = \sum_{i = 1}^{n} x_{i} y_{i}

標本レベルの話#

$n$ 個の観測値からなるベクトル $x = (x_{1}, x_{2}, \dots, x_{n})^{⊤}$ と $y = (y_{1}, y_{2}, \dots, y_{n})^{⊤}$ があるとする。

またそれらから平均値 $\bar{x}, \bar{y}$ を引いたベクトルを $\bar{x} = (x_{1} - \bar{x}, x_{2} - \bar{x}, \dots, x_{n} - \bar{x})^{⊤}$ 、 $\bar{y} = (y_{1} - \bar{y}, y_{2} - \bar{y}, \dots, y_{n} - \bar{y})^{⊤}$ とする。

標本共分散 $\hat{Cov}$ は

\hat{Cov} = \frac{1}{N} \sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y}) = \frac{1}{N} ⟨ \bar{x}, \bar{y} ⟩

$x, y$ それぞれの標本標準偏差は

\begin{array}{r} \begin{aligned} {\hat{σ}}_{x} & = \sqrt{\frac{1}{N} \sum_{i = 1}^{n} (x_{i} - \bar{x})^{2}} = \sqrt{\frac{1}{N} \sum_{i = 1}^{n} {\bar{x}}^{2}} = \sqrt{\frac{1}{N} ⟨ \bar{x}, \bar{x} ⟩} \\ {\hat{σ}}_{y} & = \sqrt{\frac{1}{N} \sum_{i = 1}^{n} (y_{i} - \bar{y})^{2}} = \sqrt{\frac{1}{N} \sum_{i = 1}^{n} {\bar{y}}^{2}} = \sqrt{\frac{1}{N} ⟨ \bar{y}, \bar{y} ⟩} \end{aligned} \end{array}

よって

\hat{r} = \frac{\hat{Cov}}{{\hat{σ}}_{x} {\hat{σ}}_{y}} = \frac{\frac{1}{N} ⟨ \bar{x}, \bar{y} ⟩}{\sqrt{\frac{1}{N} ⟨ \bar{x}, \bar{x} ⟩} \sqrt{\frac{1}{N} ⟨ \bar{y}, \bar{y} ⟩}} = \frac{⟨ \bar{x}, \bar{y} ⟩}{‖ \bar{x} ‖ \cdot ‖ \bar{y} ‖}

したがってコーシー・シュワルツの定理

- 1 \leq \frac{⟨ a, b ⟩}{‖ a ‖ \cdot ‖ b ‖} \leq 1

より、相関係数の範囲は $[- 1, 1]$ に収まる。

期待値と内積#

つづいて母集団レベルの話。

確率変数 $X, Y$ を $L^{2}$ 空間の要素（確率空間上の二乗可積分な関数）とすると、その積の期待値 $E [X Y]$ は内積の性質を満たす。

(1) $⟨ X, Y ⟩ = E [X Y] = E [Y X] = ⟨ Y, X ⟩$

(2) $⟨ X + Y, Z ⟩ = ⟨ X, Z ⟩ + ⟨ Y, Z ⟩$

(3) $⟨ k X, Y ⟩ = k ⟨ X, Y ⟩ (k \in R)$

(4) $⟨ X, X ⟩ = E [X^{2}] ≧ 0$ かつ $E [X^{2}] = 0 ⟺ X = 0 a.s.$

相関係数の導出#

コーシー・シュワルツの不等式の内積 $⟨ a, b ⟩$ を確率変数 $A, B$ の積の期待値 $E [A B]$ に置き換える。ノルムは例えば確率変数 $X$ について $‖ X ‖ = \sqrt{⟨ X, X ⟩} = E [X^{2}]$ と置き換える。こうしてコーシー・シュワルツの不等式を置き換えた

| E [A B] |^{2} \leq E [A^{2}] E [B^{2}]

を用いる。

A = (X - E [X]), B = (Y - E [Y])

とおくと

\begin{array}{r} \begin{matrix} | E [(X - E [X]) (Y - E [Y])] |^{2} \leq E [(X - E [X])^{2}] E [(Y - E [Y])^{2}] \\ ⟺ | Cov (X, Y) |^{2} \leq Var (X) Var (Y) \\ ⟺ - 1 \leq \frac{Cov (X, Y)}{\sqrt{Var (X)} \sqrt{Var (Y)}} \leq 1 \end{matrix} \end{array}

幾何学的解説#

（出所：Pearson correlation coefficient - Wikipedia）

注意点#

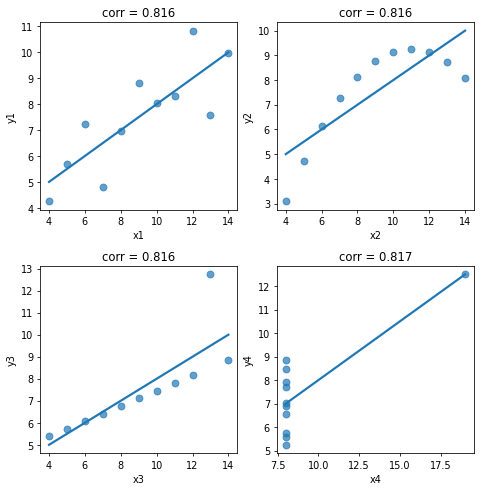
データの関係性をざっくり表すのが相関係数の良さだが、散布図でみると全然異なるデータであってもたまたま同じ相関係数になることがある。また外れ値にひっぱられる特性もある。

下の図はアンスコムの例と呼ばれる、線形回帰をしたときに同じ傾き係数になるデータセット。相関係数だと線形回帰と違って切片部分がないため係数は若干異なるがだいたい同じになる。

../_images/eb74a7dc27c8ee0544701ccf4007eb5cdd322b852637dfe47d6654ae3946b0db.png