NOTEARS#
NOTEARS(Zheng et al., 2018) は、因果探索を“勾配最適化”として解くことに成功した画期的な手法であり、伝統的な PC(制約ベース)や GES(スコアベース)とは異なる第3のアプローチとして注目されている。
従来の因果探索は
PC:条件付き独立性検定
GES:BIC などのスコアによる組合せ探索
のように 離散最適化 をベースにして因果探索を行う。
NOTEARS はこれを捨て、
“DAG である”という制約そのものを連続最適化できるようにした。
モデル:線形 SEM#
NOTEARS は、次の線形構造方程式モデル(SEM)を仮定する
\(W\) の非ゼロ要素 \(W_{ij}\) がエッジ \(j \rightarrow i\) の因果効果を表す
\(W\) を推定することが、因果グラフを推定することに相当する
DAGを連続最適化問題へ転換#
DAG とはサイクルのない有向グラフであるが、サイクル存在の有無は離散的であり、最適化には扱いにくい。
NOTEARS はこれを 微分可能な制約として次のように表す。
\(e^{A}\) は行列指数
\(W\circ W\) は アダマール積(要素ごとの積)
\(h(W)=0\) が W が DAG を表すための必要十分条件となる
この \(h(W)\) は滑らかであり、微分可能であるため、通常の連続最適化(L-BFGS, Adam 等)で扱える。
最適化#
最適化するパラメータは \(W\) であり、目的関数は次のように与えられる。
最初の項は 再構成誤差(平方誤差)
\(\lambda \|W\|_1\) は スパース化のための L1 正則化
\(h(W)=0\) が DAG 制約
したがって NOTEARS は
「誤差を最小化しつつ DAG を保つ \(W\)」
を連続最適化の枠組みで求める手法である。
実践#
gCastle パッケージにはNOTEARSの計算を効率化させたGOLEMの実装がある
from castle.common import GraphDAG
from castle.metrics import MetricsDAG
from castle.datasets import load_dataset
from castle.algorithms import GOLEM
X, true_dag, _ = load_dataset(name='IID_Test')
algo = GOLEM()
algo.learn(X)
# plot DAG
GraphDAG(algo.causal_matrix, true_dag)
# calc Metrics
met = MetricsDAG(algo.causal_matrix, true_dag)
print(met.metrics)
2025-12-09 22:41:34,080 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/backend/__init__.py[line:36] - INFO: You can use `os.environ['CASTLE_BACKEND'] = backend` to set the backend(`pytorch` or `mindspore`).
2025-12-09 22:41:34,110 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/__init__.py[line:36] - INFO: You are using ``pytorch`` as the backend.
2025-12-09 22:41:34,117 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/datasets/simulator.py[line:270] - INFO: Finished synthetic dataset
2025-12-09 22:41:34,505 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:119] - INFO: GPU is available.
2025-12-09 22:41:35,734 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:190] - INFO: Started training for 100000 iterations.
2025-12-09 22:41:35,794 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 0] score=67.199, likelihood=67.199, h=0.0e+00
2025-12-09 22:41:41,158 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 5000] score=50.079, likelihood=49.589, h=5.0e-04
2025-12-09 22:41:46,999 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 10000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:41:52,102 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 15000] score=50.070, likelihood=49.577, h=3.9e-04
2025-12-09 22:41:58,330 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 20000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:42:11,319 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 25000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:42:14,703 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 30000] score=50.070, likelihood=49.577, h=3.7e-04
2025-12-09 22:42:20,293 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 35000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:42:25,940 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 40000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:42:30,515 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 45000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:42:36,018 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 50000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:42:41,082 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 55000] score=50.070, likelihood=49.577, h=3.9e-04
2025-12-09 22:42:46,971 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 60000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:42:51,895 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 65000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:42:55,574 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 70000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:43:00,584 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 75000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:43:06,060 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 80000] score=50.070, likelihood=49.577, h=3.7e-04
2025-12-09 22:43:20,247 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 85000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:43:23,749 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 90000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:43:28,990 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 95000] score=50.070, likelihood=49.577, h=3.8e-04
2025-12-09 22:43:34,254 - /home/mitama/notes/.venv/lib/python3.10/site-packages/castle/algorithms/gradient/notears/torch/golem.py[line:203] - INFO: [Iter 100000] score=50.070, likelihood=49.577, h=3.6e-04
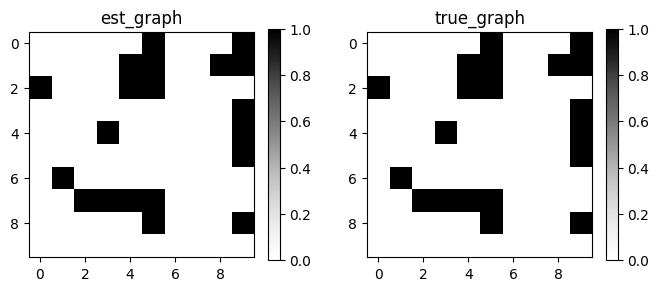
{'fdr': 0.0, 'tpr': 1.0, 'fpr': 0.0, 'shd': 0, 'nnz': 20, 'precision': 1.0, 'recall': 1.0, 'F1': 1.0, 'gscore': 1.0}