ロジカルシンキング

ロジカルシンキング#

ロジカルシンキング（Logical Thinking） は物事を論理的に筋道立てて考え、矛盾のない結論を導く思考法のこと。

論理展開の基本パターン#

帰納法#

個別の観察事実やデータから事例の共通点を取り出して一般的な法則・仮説を導く推論。

形式

  • 観察1：Aは性質Xをもつ（例：「このカラスは黒い」）

  • 観察2：Bは性質Xをもつ（例：「このカラスは黒い」）

  • 観察3：Cは性質Xをもつ（例：「このカラスは黒い」）

  • 結論：すべて（多く）の対象は性質Xをもつだろう（例：「すべてのカラスは黒いだろう」）

特徴

  • 結論は確率的・暫定的（反例で覆る可能性あり）

    • 例：アルビノの白いカラスもいるため「すべてのカラスが黒」という推論は誤り

  • 仮説生成や探索に向く

演繹法#

一般的な法則・前提から、個別の結論を必然的に導く推論。

形式

  • 前提1：すべてのAはBである（例：「すべての人間は死ぬ」）

  • 前提2：CはAである（例：「ソクラテスは人間である」）

  • 結論：CはBである（例：「ソクラテスは死ぬ」）

特徴

  • 論理的・形式的

  • 前提が正しければ、結論は必ず正しい

  • 検証・説明に向く

情報の整理・構造化のフレームワーク#

フレームワーク としてはロジックツリーないしピラミッドストラクチャーがよく用いられる

ロジックツリー#

問題を木構造に分割して整理する。

例：「売上を上げる方法」

→ 売上 = 客数 × 客単価 × 購買頻度、と構成要素を分解していき、各要素に対する施策を検討。

Hide code cell source

 
import base64
from IPython.display import Image, display

def mm_ink(graphbytes):
    """Mermaid形式のグラフ（バイト列）から、画像生成用のURLを返す。"""
    base64_bytes = base64.b64encode(graphbytes)
    base64_string = base64_bytes.decode("utf-8")
    return "https://mermaid.ink/img/" + base64_string

def mm_display(graphbytes):
    """Mermaid形式のグラフ（バイト列）を受け取り、画像として表示する。"""
    display(Image(url=mm_ink(graphbytes)))

def mm(graph):
    """Mermaid形式のグラフ文字列を受け取り、画像として表示する。"""
    graphbytes = graph.encode("utf-8")  # ← 日本語対応
    mm_display(graphbytes)

def mm_link(graph):
    """Mermaid形式のグラフ文字列から、表示用のURLを返す。"""
    graphbytes = graph.encode("utf-8")  # ← 日本語対応
    return mm_ink(graphbytes)

def mm_path(path):
    """Mermaid形式のグラフを含むファイルを読み込み、画像として表示する。"""
    with open(path, 'rb') as f:
        graphbytes = f.read()
    mm_display(graphbytes)

mm("""
graph LR;
    A["利益"] --> B["売上"]
    A --> C["費用"]
    B --> D["販売数量"]
    B --> E["単価"]
    C --> F["変動費"]
    C --> G["固定費"]
""")

ロジックツリー作成のポイント

  1. 同じレイヤーは同じカテゴリや同じ粒度の概念に揃える

  2. 100%ルール

    • 分割した子ノードを足し合わせたら親ノードと合致するか？親ノードを抜け漏れなく分解できているか？を確認する

    • 「その他」の子ノードを適度に活用する（濫用はいけないが、細かい要素も全部挙げていったらキリがない）

  3. 7 x 7 ルール

    • 深さは最大7まで、枝も最大で7個までにする

ロジックツリーの軸の切り方の観点

🧩構成要素で分ける / 🔢数式で分ける

構成要素で分ける

  • 例：顧客タイプ（個人 / 法人）

KPIなど数式で構成要素を表せるものは特に分けやすい

  • 例：売上

    • 売上＝客数 × 客単価

      • 客数＝来店数 × 成約率

      • 客単価＝単価 × 購入点数

  • 例：生産性

    • 生産性＝アウトプット量 / インプット量

🌍️空間で分ける

  • 例：

    • 地域（東日本 / 西日本）

⏱️時系列・手順

  • 時系列性・順序性がある要素で分ける

  • 例：

    • 業務フローの手順

    • プロジェクトのフェーズ（データ収集 → 前処理 → 分析 → レポート）

    • 顧客行動プロセス（認知 → 検討 → 購入 → 継続）など

MECE（ミーシー）#

MECE（Mutually Exclusive, Collectively Exhaustive） ：漏れがなく、重複もないこと。

ある物事を考えるときにロジックツリーを使う場合、漏れなくダブりなく要素を分解する必要がある。
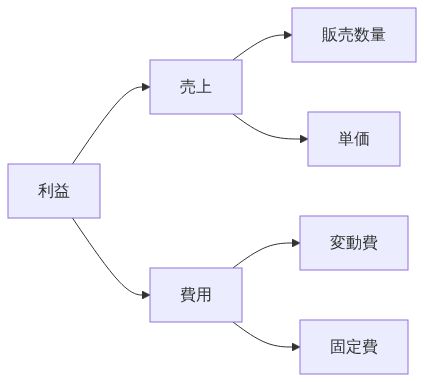
例えば「利益」を構成する枝は「売上」「費用」なら妥当だが（利益 = 売上 - 費用のため）、費用が欠けていたり、「売上」「費用」「コスト」と重複があっても不適切

ピラミッドストラクチャー#

ピラミッドストラクチャー ：結論をトップに置き、その下に理由・根拠を階層的に整理。

So What／Why So

ピラミッドストラクチャーをセルフチェックするための問い

So What（だからなんなのか） ：前提を元に導かれる結論を考えるための問い
Why So（なぜそう言えるのか） ：結論が導かれる道筋を確かめるための問い

伝え方 - ロジカルコミュニケーション#

ロジカルシンキングに相手の視点（相手が持っている情報、相手が考える前提）も考慮して、論理的に伝える技法がロジカルコミュニケーション。

PREP法#

P（Point：結論）→ R（Reason：理由）： → E（Example：具体例） → P（Point：再度結論）

の流れで話す方法。

例:
結論（P）：この提案を採用すべきです。
理由（R）：コストを30％削減できるからです。
具体例（E）：同様の施策を行ったA社では、年間2億円のコスト削減に成功しています。
再結論（P）：したがって、当社でも導入を進めるべきです。
Contents