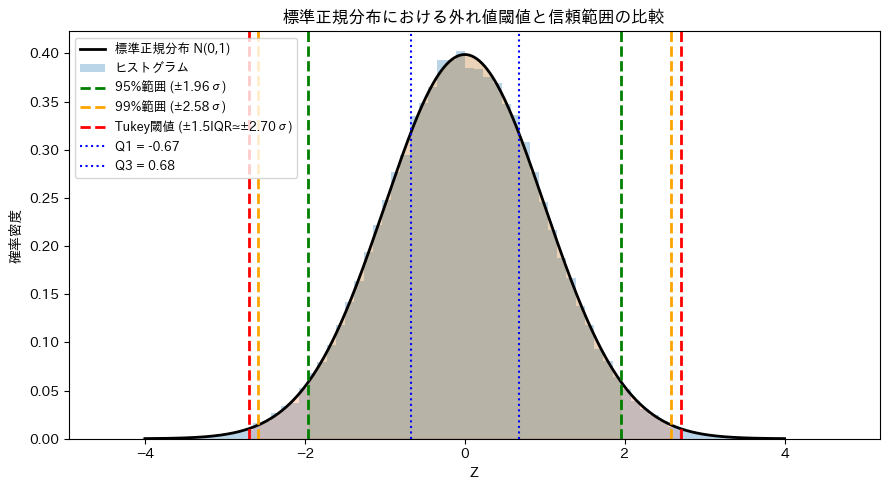
import numpy as np
import matplotlib_fontja
import matplotlib.pyplot as plt
import scipy.stats as st
# 標準正規分布データ
rng = np.random.default_rng(0)
data = rng.normal(0, 1, 100_000)
# 四分位数とIQR
q1, q3 = np.percentile(data, [25, 75])
iqr = q3 - q1
lower = q1 - 1.5 * iqr
upper = q3 + 1.5 * iqr
# 各範囲
limits = {
"95%範囲 (±1.96σ)": (-1.96, 1.96),
"99%範囲 (±2.58σ)": (-2.58, 2.58),
"Tukey閾値 (±1.5IQR≃±2.70σ)": (lower, upper),
}
# 確率密度
x = np.linspace(-4, 4, 500)
pdf = st.norm.pdf(x)
# 図を描画
plt.figure(figsize=(9, 5))
plt.plot(x, pdf, 'k-', lw=2, label="標準正規分布 N(0,1)")
plt.hist(data, bins=80, density=True, alpha=0.3, label="ヒストグラム")
# 範囲線の描画
colors = {"95%範囲 (±1.96σ)": "green", "99%範囲 (±2.58σ)": "orange", "Tukey閾値 (±1.5IQR≃±2.70σ)": "red"}
for label, (lo, hi) in limits.items():
plt.axvline(lo, color=colors[label], linestyle='--', lw=2)
plt.axvline(hi, color=colors[label], linestyle='--', lw=2, label=label)
plt.fill_between(x, 0, pdf, where=(x >= lo) & (x <= hi), color=colors[label], alpha=0.1)
# 四分位数線
plt.axvline(q1, color='blue', linestyle=':', lw=1.5, label=f"Q1 = {q1:.2f}")
plt.axvline(q3, color='blue', linestyle=':', lw=1.5, label=f"Q3 = {q3:.2f}")
plt.title("標準正規分布における外れ値閾値と信頼範囲の比較")
plt.xlabel("Z")
plt.ylabel("確率密度")
plt.legend(loc="upper left", fontsize=9)
plt.tight_layout()
plt.show()
# 数値表示
print(f"Q1 = {q1:.3f}, Q3 = {q3:.3f}, IQR = {iqr:.3f}")
print(f"Tukey下限 = {lower:.3f}, 上限 = {upper:.3f}")