LiNGAM#
LiNGAM(Linear Non-Gaussian Acyclic Model) は関数因果モデルに基づく因果探索の代表的な手法で、
構造方程式モデル(線形モデル)で
誤差項が非ガウスに従う
非巡回(Acyclic)グラフを推定する
といった前提をおく手法(Shimizu et al., 2006)
誤差項が非ガウスだとどうなるのか#
例えば観測変数\(X, Y\)と誤差変数\(\varepsilon, \varepsilon_Y\)があり、\(X\to Y\)なのか\(X\leftarrow Y\)なのかを特定したいとする。 それぞれの方向についての線形回帰モデル \(Y = b X + \varepsilon\) と \(X= b_Y Y + \varepsilon_Y\) を構築して残差を計算して違いを見るとする。 誤差項がガウス分布に従うとき(Case1)は、残差が左右対称で2つのモデルで違いがわからない。しかし一様分布(Case2)などでは残差の分布に差が出てくる。
LiNGAMではこの非対称性を利用して因果の方向を探索していく。
ガウス分布は平均ベクトルと分散共分散行列が決まると分布の形が一意に決まる特殊な分布。そのため非ガウスであればLiNGAMは適用可能。
LiNGAMのアルゴリズム#
大きく4つのステップになる
セミパラメトリックなSEMの構築
独立成分分析
因果的順序の定義
因果関係・因果効果の推定
1. セミパラメトリックなSEMの構築#
LiNGAMではSEM(構造方程式モデリング、線形回帰モデルや因子分析などを一般化した線形モデル)で記述する。つまり、関数形として線形モデルを仮定する。
モデル#
OutcomeもTreatmentもCovariatesも区別無く、変数を全部\(x_i\)で表現する。
ここで\(b_{ij}\)は因果効果を表す係数で、\(\varepsilon_i\)は誤差項。
行列で表すと:
ここで\(B\)は因果効果を表す係数の行列。
※非巡回の制約があるため、因果の流れの通りに(最上流を\(x_1\)、最下流を\(x_3\)に)変数を並べると係数行列\(B\)が下三角行列になる
例:outcomeを\(x_3\)とし、\(x_1, x_2\)をTreatmentとする。
この構造方程式モデルを行列表記にすると
となる。係数行列を\(B\)とおき、それ以外もベクトルにすると
となる。
セミパラメトリックとは#
セミパラメトリックとは、関数形には仮定をおく一方で外生変数の分布には仮定を置かないという意味。LiNGAMは外生変数(誤差変数)は非ガウスと仮定はするが、具体的な分布型については仮定を置かない(ガウス分布以外ならなんでもいい)のでセミパラメトリックモデルに分類される。
非ガウス性をどう確かめるか#
一般的な方法は:
データをヒストグラムなどに可視化して観察する
尖度と歪度の計算(ガウス分布の場合、尖度は3、歪度は0)
統計的検定の実施(シャピロ・ウィルク検定、コルモゴロフ-スミルノフ検定など)
2. 独立成分分析#
係数行列の推定のために、独立成分分析を使う。
モデルの変形#
を変形すると
(ここで\(I\)は単位行列)
\(A := (I - B)^{-1}\) とおくと
となるので、この\(A\)を求めれば良い。\(A\)の推定では独立成分分析を使用する。
求めたら、\(A^{-1} = I - B\) なので \(B= I - A^{-1}\) を計算して\(B\)を求める
独立成分分析#
主成分分析はもとのデータを各変数の相関が0になるような新しい変数に変換する手法。
ガウス分布に従うデータなら、主成分分析で変数間の関係が独立になる。
非ガウス分布に従うデータだと相関は0になるが独立にはならない。
独立成分分析は主成分分析の結果\(x_{pca}\)に対して線形変換を施して新たな変数\(x_{ica}\)を作成する。
という分解ができるため、LiNGAMではこれを使う。
ただし、\(B\)が下三角行列なので、\(A^{-1}\)は対角成分が1で、対角成分より上側のすべての要素が0である必要があり、独立成分分析の後にそうした後処理が必要になる
3. 因果的順序の推定#
ICA は独立成分の順序を決めないため、誤差成分の順序(=因果順序)を復元する必要がある。
LiNGAM では次の条件を満たすように並べ替える。
\(B = I - A^{-1}\) が下三角行列(あるいは下三角に近い構造)になるように、列(成分の順序)を並べ替える。
これは、DAG の性質(因果順序が存在し、上から下へ流れる)を利用したものである。
より具体的には:
\(A^{-1}\) の対角成分がすべて非零となるように列順序を変更し
\(B = I - A^{-1}\) が非巡回的(下三角)になるような順序を探索する
ここが LiNGAM 特有のステップであり、ICA の識別性のギャップを埋める働きをする。
LiNGAMの計算手順のイメージ#
※ 小川(2020)と同じように実装したはずだが、一部符号が反転してて、あまりうまくいかなかった
1.データを生成
# 適当にデータを生成する
import numpy as np
import pandas as pd
def gen_data():
n = 1000
np.random.seed(0)
# 非ガウスの誤差
e1 = np.random.uniform(size=n)
e2 = np.random.uniform(size=n)
e3 = np.random.uniform(size=n)
# 係数行列
B = np.array([
[0, 0, 0],
[3, 0, 0],
[4, 5, 0],
])
# 各変数の生成
x1 = e1
x2 = B[1, 0]*x1 + e2
x3 = B[2, 0]*x1 + B[2, 1]*x2 + e3
# DFにする
df = pd.DataFrame({"x1": x1, "x2": x2, "x3": x3})
return df, B
df, B = gen_data()
2.独立成分分析
ここではscikit-learnのFastICAを使ってみる。
from sklearn.decomposition import FastICA
ica = FastICA(random_state=0, max_iter=1000).fit(df)
# ICAで求めた行列A
A_ica = ica.mixing_
A_ica_inv = np.linalg.inv(A_ica)
A_ica_inv.round(1)
array([[ 13.8, 17.5, -3.5],
[ 2.9, -0.7, 0.1],
[-10.1, 3.3, 0. ]])
3.因果的順序の推定
\(A_{ica}^{-1}\)に対して
行の順番を変換
行の大きさを調整
して対角成分が1で対角成分より上側の要素が全部0な行列になるようにする
munkresパッケージのハンガリアンアルゴリズムという対角成分の和を最小にする問題を解く
# 1. 行の順番を変換
# 絶対値の逆数にして、対角成分の和を最小化する問題に置き換える
A_ica_inv_small = 1 / np.abs(A_ica_inv)
# 対角成分の和を最小にする行の入れ替えを行う
from munkres import Munkres
m = Munkres()
ixs = np.vstack(m.compute(A_ica_inv_small))
# 順番の入れ替え
ixs = ixs[np.argsort(ixs[:, 0]), :]
ixs_perm = ixs[:, 1]
A_ica_inv_perm = np.zeros_like(A_ica_inv)
A_ica_inv_perm[ixs_perm] = A_ica_inv
# 2. 行の大きさを調整
# 対角成分が1になるよう調整
A_ica_inv_perm_adjusted = A_ica_inv_perm / np.diag(A_ica_inv_perm)
A_ica_inv_perm_adjusted.round(1)
array([[ 1. , -0.2, -0. ],
[-3.5, 1. , -0. ],
[ 4.8, 5.3, 1. ]])
\(A^{-1} = I - B\)なので\(B= I - A^{-1}\)として\(B\)を求める
I = np.eye(3)
B = I - A_ica_inv_perm_adjusted
B.round(1)
array([[ 0. , 0.2, 0. ],
[ 3.5, 0. , 0. ],
[-4.8, -5.3, 0. ]])
gCastleパッケージで実装#
gCastleパッケージには ICAベースのLiNGAMも実装されている
from castle.common import GraphDAG
from castle.metrics import MetricsDAG
from castle.datasets import load_dataset
from castle.algorithms import ICALiNGAM
X, true_dag, _ = load_dataset(name='IID_Test')
algo = ICALiNGAM()
algo.learn(X)
# plot DAG
GraphDAG(algo.causal_matrix, true_dag)
# calc Metrics
met = MetricsDAG(algo.causal_matrix, true_dag)
print(met.metrics)
2026-03-11 22:11:44,662 - /home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/castle/backend/__init__.py[line:36] - INFO: You can use `os.environ['CASTLE_BACKEND'] = backend` to set the backend(`pytorch` or `mindspore`).
2026-03-11 22:11:44,829 - /home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/castle/algorithms/__init__.py[line:36] - INFO: You are using ``pytorch`` as the backend.
2026-03-11 22:11:44,833 - /home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/castle/datasets/simulator.py[line:270] - INFO: Finished synthetic dataset
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/sklearn/decomposition/_fastica.py:127: ConvergenceWarning: FastICA did not converge. Consider increasing tolerance or the maximum number of iterations.
warnings.warn(
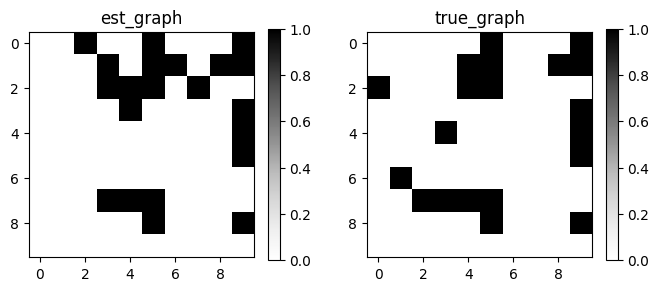
{'fdr': 0.2857, 'tpr': 0.75, 'fpr': 0.24, 'shd': 7, 'nnz': 21, 'precision': 0.7143, 'recall': 0.75, 'F1': 0.7317, 'gscore': 0.45}
lingamパッケージで実践#
Pythonだとlingamパッケージがある
独立成分分析を使う元祖のLiNGAMは実装されておらず、その高速板のDirectLiNGAMや、時期列要素を加味したVAR-LiNGAMなど派生手法が提供されている
Tutorial: DirectLiNGAM — LiNGAM 1.8.2 documentation
df, true_B = gen_data()
import lingam
model = lingam.DirectLiNGAM()
model.fit(df)
# adjacency_matrix_ で推定した係数行列Bを見ることができる
print("Estimate:")
print(model.adjacency_matrix_.round(1))
print("True:")
print(true_B)
Estimate:
[[0. 0. 0. ]
[3. 0. 0. ]
[3.9 5. 0. ]]
True:
[[0 0 0]
[3 0 0]
[4 5 0]]
LiNGAMの派生手法#
ICA-LiNGAM (Shimizu et al., 2006) :元祖 LiNGAM。ICA による分離と順序復元で因果推定。
DirectLiNGAM (Shimizu et al., 2011) :独立性の強さに基づき、直接因果順序を特定する高速版。
ParceLiNGAM (Tashiro et al., 2014) :未観測の共通原因(潜在変数)を考慮して因果構造を推定。
GroupLiNGAM (Shimizu et al., 2011) :変数がグループ構造を持つ場合の因果推定。
VAR-LiNGAM (Hyvärinen et al., 2010) :時系列(VAR)データ向けの因果推定。
Bayesian LiNGAM (Matsui et al., 2012) :ベイズ推論により不確実性を扱う LiNGAM。
Kernel LiNGAM (Kano & Shimizu, 2003 → LiNGAM 系に応用) :カーネル法で非線形因果を扱う。
Robust LiNGAM (Shimizu & Bollen, 2014) :外れ値・重い尾分布にロバストな LiNGAM。
参考文献#
小川雄太郎. (2020). つくりながら学ぶ! Python による因果分析. マイナビ出版.
清水昌平(2017)統計的因果探索
-
NTTコミュニケーションズの教材。理論面含めて詳しい話がある