MIC（Maximal Information Coefficient）

MIC（Maximal Information Coefficient）#

Reshef, et al. (2011). Detecting novel associations in large data sets. で提案されたMIC（Maximal Information Coefficient）は、相互情報量を用いてデータの非線形な関連性を評価できる係数。

「21世紀の相関係数（A Correlation for the 21st Century）」としてScience誌に紹介され、話題になった。

相互情報量（Mutual Information; MI）#

確率分布 \(p(x,y)\) による一般の非線形依存関係の強さを測る。

定義式#

離散確率変数の場合：

\[ I(X ; Y)=\sum_{y \in \mathcal{Y}} \sum_{x \in \mathcal{X}} p(x, y) \log \frac{p(x, y)}{p(x) p(y)} \]

連続確率変数の場合：

\[ I(X ; Y)=\int_{\mathcal{Y}} \int_{\mathcal{X}} p(x, y) \log \frac{p(x, y)}{p(x) p(y)} d x d y \]

特徴#

  • \(I(X;Y)=0\) なら 独立

  • 線形・非線形を問わずあらゆる依存を検出

  • ただし値域が固定されておらず、相関係数のように簡単には解釈できない

  • 推定には KDE, kNN などが必要

Hide code cell source

 
import numpy as np
from sklearn.metrics import mutual_info_score # 離散型確率変数の相互情報量

def discretized_mi(x, y, bins=20):
    # 連続変数を離散化して簡易的に相互情報量を求める
    # x, y を bins 個の等幅ビンに離散化
    x_binned = np.digitize(x, np.histogram_bin_edges(x, bins=bins))
    y_binned = np.digitize(y, np.histogram_bin_edges(y, bins=bins))
    
    # 離散化した値で MI を計算
    return mutual_info_score(x_binned, y_binned)

import matplotlib.pyplot as plt
fig, axes = plt.subplots(figsize=[10, 2.5], ncols=3)

true_r = 0
mu = np.array([0.0, 0.0])
Sigma = np.array([[1.0, true_r], [true_r, 1.0]])
samples = np.random.multivariate_normal(mu, Sigma, size=100)
x = samples[:, 0]
y = samples[:, 1]
axes[0].scatter(x, y)
axes[0].set_title(f"Mutual Info = {discretized_mi(x, y):.3f}")

x = np.linspace(-10, 10, 15)
y = 1 / (1 + np.exp(-x))
axes[1].scatter(x, y)
axes[1].set_title(f"Mutual Info = {discretized_mi(x, y):.3f}")

x = np.linspace(-3.14,3.14, 100)
y = x**2 + np.random.random(len(x))
axes[2].scatter(x, y)
axes[2].set_title(f"Mutual Info = {discretized_mi(x, y):.3f}")

%matplotlib inline
../../../_images/a0c5d68af08fa79798c23ec7eb5c12118438c0d1c091dce0852b2383da8f3c68.png

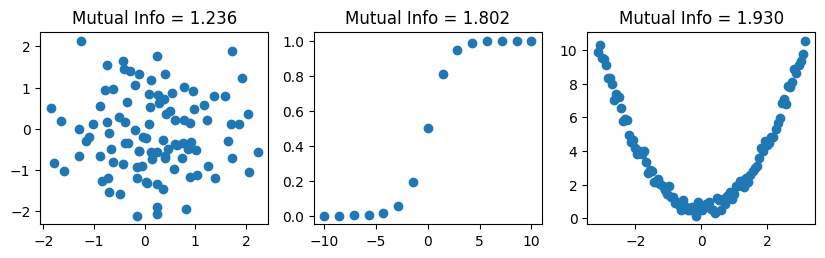
MIC（Maximal Information Coefficient）#

概念的な定義#

散布図をさまざまな格子分割 \((x,y)\) に切り、各ビンの相対頻度から 相互情報量 を計算し、その最大値をスケール正規化したもの。

MIC は相互情報量を複数グリッドで最大化し、

\[ 0 \le \mathrm{MIC} \le 1 \]

となるように正規化した指標。

特徴#

  • 単調・非単調のどちらも検出

  • 関係の形状が分からない探索フェーズに強い

  • 計算はやや重いが実務では十分使える

参考#

Contents