ベクトル自己回帰（VAR）モデル#
VARはARモデルの拡張版であり、VAR(\(p\))モデルは\(y_t\)を定数と自身の\(p\)次のラグ（\(p\)期の過去の値）に回帰したモデル。
モデル#
変数が\(n\)次元、ラグの次数が\(p\)だとする。（例えば時点\(t\)の観測値は \(y_{1,t}, y_{2,t}, \dots, y_{n,t}\) となる。）
VAR(\(p\)) では、各変数 \(y_{i,t}\) は、すべての変数の過去 \(p\) 期分の線形結合で表される。
VAR(\(p\))
\[
y_{i,t}
=
c_{i}
+
\sum_{k=1}^{p}
\sum_{j=1}^{n}
\phi_{ij}^{(k)} \, y_{j,t-k}
+
\varepsilon_{i,t}
\quad
(i = 1,\dots,n)
\]
\(\phi_{ij}^{(k)}\)：変数 \(j\) の \(k\) 期前」が「変数 \(i\) の現在」に与える影響
\(\varepsilon_{i,t}\)：変数 \(i\) に対応する誤差項
もう少しベクトルや行列を使って表すと、
VAR(\(p\)) （行列を使った表現）
\[
\mathbf{y}_t
= \mathbf{c} + \sum_{k=1}^p \boldsymbol{\Phi}_k \mathbf{y}_{t-k}+\varepsilon_t
,\quad \varepsilon_t \sim \text { W.N.} (\boldsymbol{\Sigma})
\]
\(\mathbf{c}\in\mathbb{R}^{n\times 1}\)
\(\boldsymbol{\Phi}_k \in\mathbb{R}^{n\times n}\)
例：2変量VAR(1)モデル
\[\begin{split}
\begin{aligned}
& \left\{\begin{array}{l}
y_{1 t}=c_1+\phi_{11} y_{1, t-1}+\phi_{12} y_{2, t-1}+\varepsilon_{1 t} \\
y_{2 t}=c_2+\phi_{21} y_{1, t-1}+\phi_{22} y_{2, t-1}+\varepsilon_{2 t}
\end{array}, \quad\binom{\varepsilon_{1 t}}{\varepsilon_{2 t}} \sim\right. \text { W.N. } \\
& \mathbf{\Sigma}=\left(\begin{array}{cc}
\sigma_1^2 & \rho \sigma_1 \sigma_2 \\
\rho \sigma_1 \sigma_2 & \sigma_2^2
\end{array}\right)
\end{aligned}
\end{split}\]
ここで \(\rho=\operatorname{Corr}\left(\varepsilon_{1 t}, \varepsilon_{2 t}\right)\)
状態ベクトル \(\mathbf{y}_t \in \mathbb{R}^n\) 、 ラグ \(k\) の係数行列 \(\boldsymbol{Phi}_k \in \mathbb{R}^{n \times n}\)、 誤差ベクトル \(\boldsymbol{\varepsilon}_t\) をそれぞれ
\[\begin{split}
\mathbf{y}_t
=
\begin{pmatrix}
y_{1,t} \\
y_{2,t} \\
\vdots \\
y_{n,t}
\end{pmatrix}
,\quad
\mathbf{\Phi}_k
=
\begin{pmatrix}
\phi_{11}^{(k)} & \phi_{12}^{(k)} & \cdots & \phi_{1n}^{(k)} \\
\phi_{21}^{(k)} & \phi_{22}^{(k)} & \cdots & \phi_{2n}^{(k)} \\
\vdots & \vdots & \ddots & \vdots \\
\phi_{n1}^{(k)} & \phi_{n2}^{(k)} & \cdots & \phi_{nn}^{(k)}
\end{pmatrix}
,\quad
\boldsymbol{\varepsilon}_t
=
\begin{pmatrix}
\varepsilon_{1,t} \\
\varepsilon_{2,t} \\
\vdots \\
\varepsilon_{n,t}
\end{pmatrix}
\end{split}\]
とおくと、VAR(\(p\)) は次のように表現できる。
VAR(\(p\)) （行列を使った表現）
\[
\mathbf{y}_t
=
\sum_{k=1}^{p}
\mathbf{\Phi}_k \mathbf{y}_{t-k}
+
\boldsymbol{\varepsilon}_t
\]
※切片を含めた表現もされる
\[
\mathbf{y}_t
=
\mathbf{c}
+
\sum_{k=1}^{p}
\mathbf{\Phi}_k \mathbf{y}_{t-k}
+
\boldsymbol{\varepsilon}_t
\]
パラメータ推定#
VARは一見複雑だが、本質的には各変数を同じ説明変数で回帰しているだけ（多変量回帰）である。例えばVAR(1) は \(\mathbf{y}_t = \mathbf{\Phi}_1 \mathbf{y}_{t-1} + \boldsymbol{\varepsilon}_t\) 。
サンプルサイズを \(T\) とする（初期 \(p\) 個は捨てる）。
目的変数行列を\(\mathbf{Y}\)、説明変数行列を\(\mathbf{Z}\)、係数行列をまとめたものを\(\mathbf{B}\)とおく。
\[\begin{split}
\mathbf{Y}
=
\begin{pmatrix}
\mathbf{y}_{p+1}^\top \\
\mathbf{y}_{p+2}^\top \\
\vdots \\
\mathbf{y}_T^\top
\end{pmatrix}
\in \mathbb{R}^{(T-p)\times n}
,\quad
\mathbf{Z}
=
\begin{pmatrix}
\mathbf{y}_{p}^\top & \mathbf{y}_{p-1}^\top & \cdots & \mathbf{y}_{1}^\top \\
\mathbf{y}_{p+1}^\top & \mathbf{y}_{p}^\top & \cdots & \mathbf{y}_{2}^\top \\
\vdots & \vdots & & \vdots \\
\mathbf{y}_{T-1}^\top & \mathbf{y}_{T-2}^\top & \cdots & \mathbf{y}_{T-p}^\top
\end{pmatrix}
,\quad
\mathbf{B}
=
\begin{pmatrix}
\mathbf{\Phi}_1^\top \\
\mathbf{\Phi}_2^\top \\
\vdots \\
\mathbf{\Phi}_p^\top
\end{pmatrix}
\end{split}\]
VARはOLSで推定可能
\[
\hat{\mathbf{B}}
=
(\mathbf{Z}^\top \mathbf{Z})^{-1}
\mathbf{Z}^\top \mathbf{Y}
\]
実装#
Vector Autoregressions tsa.vector_ar - statsmodels 0.14.6
import numpy as np
import pandas
import statsmodels.api as sm
from statsmodels.tsa.api import VAR
mdata = sm.datasets.macrodata.load_pandas().data
# prepare the dates index
dates = mdata[['year', 'quarter']].astype(int).astype(str)
quarterly = dates["year"] + "Q" + dates["quarter"]
from statsmodels.tsa.base.datetools import dates_from_str
quarterly = dates_from_str(quarterly)
mdata = mdata[['realgdp', 'realcons']]
mdata.index = pandas.DatetimeIndex(quarterly)
data = np.log(mdata).diff().dropna()
# data
display(data.tail())
# make a VAR model
model = VAR(data)
results = model.fit(2)
results.summary()
| realgdp | realcons | |
|---|---|---|
| 2008-09-30 | -0.006781 | -0.008948 |
| 2008-12-31 | -0.013805 | -0.007843 |
| 2009-03-31 | -0.016612 | 0.001511 |
| 2009-06-30 | -0.001851 | -0.002196 |
| 2009-09-30 | 0.006862 | 0.007265 |
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/statsmodels/tsa/base/tsa_model.py:473: ValueWarning: No frequency information was provided, so inferred frequency QE-DEC will be used.
self._init_dates(dates, freq)
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Fri, 02, Jan, 2026
Time: 16:14:49
--------------------------------------------------------------------
No. of Equations: 2.00000 BIC: -20.0648
Nobs: 200.000 HQIC: -20.1630
Log likelihood: 1465.40 FPE: 1.63813e-09
AIC: -20.2297 Det(Omega_mle): 1.55920e-09
--------------------------------------------------------------------
Results for equation realgdp
==============================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------------
const 0.001024 0.000971 1.055 0.291
L1.realgdp -0.096477 0.087307 -1.105 0.269
L1.realcons 0.571453 0.102953 5.551 0.000
L2.realgdp -0.038461 0.081226 -0.474 0.636
L2.realcons 0.352325 0.109914 3.205 0.001
==============================================================================
Results for equation realcons
==============================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------------
const 0.004668 0.000843 5.538 0.000
L1.realgdp 0.051847 0.075826 0.684 0.494
L1.realcons 0.194414 0.089414 2.174 0.030
L2.realgdp 0.013699 0.070545 0.194 0.846
L2.realcons 0.181398 0.095460 1.900 0.057
==============================================================================
Correlation matrix of residuals
realgdp realcons
realgdp 1.000000 0.603188
realcons 0.603188 1.000000
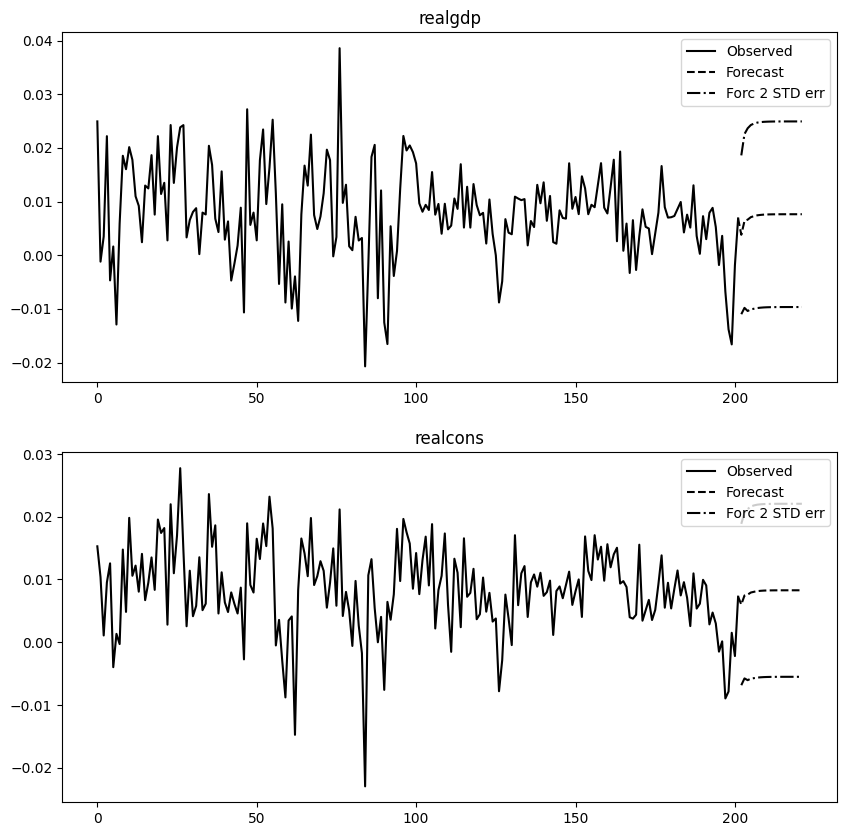
_ = results.plot_forecast(steps=20)
