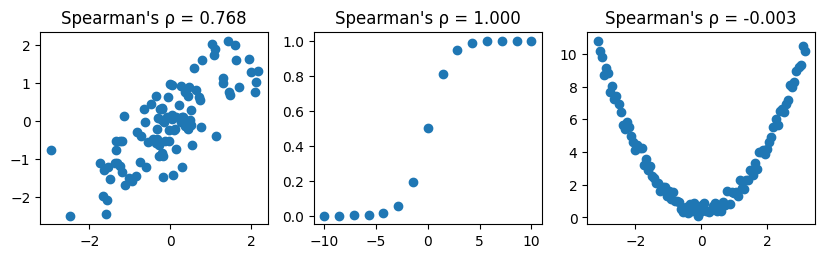
Spearman の順位相関係数（Spearman’s ρ）

Contents

Spearman の順位相関係数（Spearman’s ρ）#

Spearmanの順位相関係数はデータの順位（rank）に基づき、単調な非線形関係を検出できる。

定義式#

\[ \rho = 1 - \frac{6\sum_{i=1}^{n} d_i^2}{n(n^2 - 1)} \]

ここで

  • \(d_i\) は \(i\) 番目の観測における \(x\) と \(y\) の順位の差

  • \(n\) はサンプルサイズ

特徴#

  • 単調（増加・減少）であれば非線形も検出できる

  • 値域は \([-1,1]\)

  • 外れ値にやや強い

Hide code cell source

 
from scipy.stats import spearmanr
import matplotlib.pyplot as plt
import numpy as np

fig, axes = plt.subplots(figsize=[10, 2.5], ncols=3)

true_r = 0.75
mu = np.array([0.0, 0.0])
Sigma = np.array([[1.0, true_r], [true_r, 1.0]])
samples = np.random.multivariate_normal(mu, Sigma, size=100)
x = samples[:, 0]
y = samples[:, 1]
axes[0].scatter(x, y)
axes[0].set_title(f"Spearman's ρ = {spearmanr(x, y).statistic:.3f}")

x = np.linspace(-10, 10, 15)
y = 1 / (1 + np.exp(-x))
axes[1].scatter(x, y)
axes[1].set_title(f"Spearman's ρ = {spearmanr(x, y).statistic:.3f}")

x = np.linspace(-3.14,3.14, 100)
y = x**2 + np.random.random(len(x))
axes[2].scatter(x, y)
axes[2].set_title(f"Spearman's ρ = {spearmanr(x, y).statistic:.3f}")

%matplotlib inline
../../../_images/19a8db2d019280569a67c08dbd92f282227a5d2516f4a7aeaabe1838c9d7173c.png
Contents