ロジスティックモデル

ロジスティックモデル#

正規累積モデルは累積分布関数を使うため、コンピュータで積分計算をするのがやや難しいという問題がある。そこでロジスティック分布に置き換えたものが使われる。

ロジスティック分布の確率密度関数と累積分布関数は

\[ f(x)=\frac{\exp (-x)}{[1+\exp (-x)]^2}, \quad F(x)=\frac{1}{1+\exp (-x)} \]

となる。とくに\(x\)を約1.7倍したロジスティック分布は累積分布関数が正規分布と非常に近くなることが知られている。

Hide code cell source

 
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, logistic
x = np.linspace(-10, 10, 1000)

fig, axes = plt.subplots(figsize=[12, 3], dpi=90, ncols=2)
ax = axes[0]
ax.plot(x, norm.pdf(x), 'k-', label='Normal Distribution')
ax.plot(x, logistic.pdf(x),  'orange', alpha=0.9, label='Logistic Distribution')

ax.set_title('Normal Distribution vs Logistic Distribution')
ax.set_xlabel('x')
ax.set_ylabel('Probability Density')
ax.legend()
ax.grid(True)

ax = axes[1]
ax.plot(x, norm.cdf(x), 'k-', label=r'CDF of $Normal(x)$')
ax.plot(x, logistic.cdf(x), 'orange', alpha=0.9, label=r'CDF of $Logistic(x)$')
ax.plot(x, logistic.cdf(x * 1.704), 'red', alpha=0.9, label=r'CDF of $Logistic(1.7 x)$')
ax.set_title('Normal Distribution vs Logistic Distribution (CDF)')
ax.set_xlabel('x')
ax.set_ylabel('Probability')
ax.legend()
ax.grid(True)
plt.show()
../../../_images/be1480d3d184ef42d63b818995b7efdef53b7fb5a1b31b8b494df28edcfe3682.png

1PLモデル（ラッシュモデル）#

正規分布の代わりにロジスティック分布を使った 1パラメータ・ロジスティック（1PL）モデル は以下のように表される。

1PLモデル

\[ P(y_{ij} = 1) = \frac{1}{1+ \exp(-D a ( \theta_i - b_j))} \]

  • \(a\)：識別力（全項目で共通）

    • \(a=1\)とおく定義もある

  • \(b_j\)：項目困難度

※なお\(D\)はロジスティック・シグモイド関数を正規累積モデルの関数に近づけるための定数（通常は\(D=1.7\)か\(D=1\)にする）なので、正規累積モデルと比較する必要がなければ不要（\(D=1\)でいい）。

1PLモデルは ラッシュモデル（Rasch model） とも呼ばれる。Raschという人がIRTとは独立に1PLモデルを提案していたため。

2PLモデル#

正規分布の代わりにロジスティック分布を使った 2パラメータロジスティック（2PL）モデル は以下のように表される。

2PLモデル

\[ P(y_{ij} = 1) = \frac{1}{1+ \exp(-D a_j ( \theta_i - b_j))} \]

  • \(a_j\)：項目識別力

  • \(b_j\)：項目困難度

Hide code cell source

 
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
theta = np.linspace(-4, 4, 1000)

fig, axes = plt.subplots(figsize=[8, 2], ncols=2)

def icc(theta, a, b):
    z = 1.7 * a * (theta - b)
    return 1 / (1 + np.exp(-z))

a = 1
for b in [-1, 0, 1]:
    axes[0].plot(theta, icc(theta, a, b), label=r"$b$ = " + f"{b}")
axes[0].set(xlabel=r"$\theta_i$", ylabel=r"$P(y_{ij} = 1)$", xticklabels=[], yticklabels=[])
axes[0].legend()
axes[0].grid(True)

b = 0
for a in [0.5, 1, 2]:
    axes[1].plot(theta, icc(theta, a, b), label=r"$a$ = " + f"{a}")
axes[1].set(xlabel=r"$\theta_i$", ylabel=r"$P(y_{ij} = 1)$", xticklabels=[], yticklabels=[])
axes[1].legend()
axes[1].grid(True)
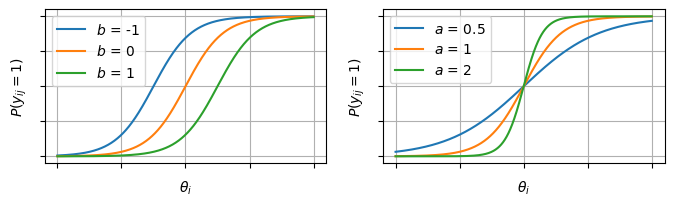
../../../_images/5cb25378f36b687235691ca9818161112b826d835a70bbd85a638b9dfab64736.png

3PLモデル#

例えば4択問題では、正解がわからなくて適当に選んだとしても1/4は当たることになる。こうした影響を「当て推量」パラメータ\(c_j\)として取り入れたモデル。

3PLモデル

\[ P(y_{ij} = 1) = c_j + \frac{1 - c_j}{1 - \exp\big(-a_j ( \theta_i - b_j) \big)} \]

  • \(a_j\)：項目識別力

  • \(b_j\)：項目困難度

  • \(c_j\)：当て推量

\(c_j\)は項目特性曲線の下限となる。\(\theta_i\)がどんなに低い人でも必ず\(c_j\)以上の\(P(y_{ij} = 1)\)になるということ。

4PLモデル#

項目特性曲線の上限を表すパラメータ\(d_j\)を追加したもの。\(\theta_i\)がどんなに高い人でも100%の正答率にはできない高難度な状況（運ゲー）を想定したモデル。

4PLモデル

\[ P(y_{ij} = 1) = c_j + \frac{d_j - c_j}{1 - \exp\big(-a_j ( \theta_i - b_j) \big)} \]

  • \(a_j\)：項目識別力

  • \(b_j\)：項目困難度

  • \(c_j\)：当て推量。項目特性曲線の下限

  • \(d_j\)：項目特性曲線の上限

4PLMになるとかなりモデルが複雑になりパラメータの推定も不安定になるので、1~3PLMほど一般的ではない。対応していないライブラリも多い。

5PLモデル#

「非対称性」のパラメータ\(e_j\)を追加したもの。4PLまでは項目特性曲線の動き方が0.5を中心に対称になっている。5PLでは「最初は\(\theta_i\)があがるほど急激に\(P(y_{ij}=1)\)が上がるが、徐々に上がりにくくなる」などの状況を表すことができる。

5PLモデル

\[ P(y_{ij} = 1) = c_j + \frac{d_j - c_j}{\left[ 1 - \exp\big(-a_j ( \theta_i - b_j) \big) \right]^{e_j}} \]

  • \(a_j\)：項目識別力

  • \(b_j\)：項目困難度

  • \(c_j\)：当て推量。項目特性曲線の下限

  • \(d_j\)：項目特性曲線の上限

  • \(e_j\)：非対称性

実装例#

# サンプルデータの生成
import numpy as np
import pandas as pd

def simulate_2pl(
    N=1000,  # 受験者数
    J=20,    # 項目数
    mu_a=0.0,
    sigma_a=0.3,
    mu_b=0.0,
    sigma_b=1.0,
    seed=42,
):
    rng = np.random.default_rng(seed)
    theta = rng.normal(0, 1, size=N)
    a = rng.lognormal(mean=mu_a, sigma=sigma_a, size=J)
    b = rng.normal(mu_b, sigma_b, size=J)
    eta = a[None, :] * (theta[:, None] - b[None, :])
    p = 1 / (1 + np.exp(-eta))
    U = rng.binomial(1, p) # 反応行列
    return {
        "U": U,
        "theta": theta,
        "a": a,
        "b": b,
        "p": p,
    }

num_users = 1000
num_items = 20
data = simulate_2pl(N=num_users, J=num_items)

df = pd.DataFrame(data["U"],
                  index=[f"user_{i+1}" for i in range(num_users)],
                  columns=[f"question_{j+1}" for j in range(num_items)])

df.head()
question_1 question_2 question_3 question_4 question_5 question_6 question_7 question_8 question_9 question_10 question_11 question_12 question_13 question_14 question_15 question_16 question_17 question_18 question_19 question_20
user_1 0 1 0 1 1 1 1 0 0 1 1 0 0 0 1 1 0 1 0 0
user_2 0 0 1 0 1 0 1 1 1 0 0 0 0 1 0 0 0 1 1 1
user_3 1 1 0 1 1 1 1 0 1 0 0 1 1 0 0 0 0 1 1 0
user_4 1 1 1 1 1 1 1 0 0 0 0 1 0 1 0 1 1 1 1 1
user_5 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 
import matplotlib.pyplot as plt
import seaborn as sns

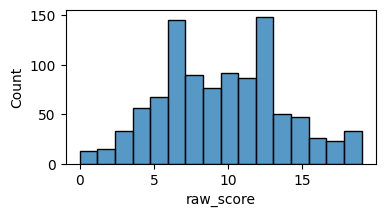
df["raw_score"] = df.sum(axis=1)

fig, ax = plt.subplots(figsize=[4,2])
sns.histplot(data=df, x="raw_score", ax=ax)

<Axes: xlabel='raw_score', ylabel='Count'>
../../../_images/3fa37f8266ff4e7b961e33723f59446a94571420058879b567d02baa5f36fcb3.png 
df["raw_score_cat"] = pd.qcut(df["raw_score"], q=5, duplicates="drop")

item_col = "question_1"
d = df.groupby("raw_score_cat")[item_col].mean().reset_index()
d["raw_score_cat"] = d["raw_score_cat"].cat.codes
fig, ax = plt.subplots(figsize=[4,2])
sns.lineplot(x="raw_score_cat", y=item_col, data=d, ax=ax)

del df["raw_score"]
del df["raw_score_cat"]

/tmp/ipykernel_10247/2308563096.py:4: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  d = df.groupby("raw_score_cat")[item_col].mean().reset_index()
../../../_images/2ba10373f6817b9c44d4f7cb719ce23924b1d3d88d305847f1840597ddacf7af.png 
# 縦持ちへ変換
df_long = pd.melt(
    df.reset_index(),
    id_vars="index",
    var_name="item",
    value_name="response",
).rename(columns={"index": "user"})
df_long.head()
user item response
0 user_1 question_1 0
1 user_2 question_1 0
2 user_3 question_1 1
3 user_4 question_1 1
4 user_5 question_1 0

モデルの定義#

注意点として、\(a\)に非負制約をかけないとMCMCが収束しにくい（\(\theta-b\)の値と\(a\)の値次第で同値の尤度が出てきて一意に決まらないので）

pm.LogNormal(mu=0.0, sigma=np.sqrt(0.5)) や pm.HalfNormal などが使われる事が多い様子

# indexと値の取得
user_idx, users = pd.factorize(df_long["user"])
item_idx, items = pd.factorize(df_long["item"])
responses = df_long["response"].to_numpy()

import pymc as pm
coords = {"user": df.index, "item": df.columns}
model = pm.Model(coords=coords)
with model:
    # 観測値の配列
    response_obs = pm.Data("responses", responses)
    # 2PLM
    a = pm.LogNormal("a", mu=0.0, sigma=np.sqrt(0.5), dims="item")
    b = pm.Normal("b", mu=0.0, sigma=1.0, dims="item")
    theta = pm.Normal("theta", mu=0.0, sigma=1.0, dims="user")
    obs = pm.Bernoulli("obs", p=pm.math.sigmoid(a[item_idx] * (theta[user_idx] - b[item_idx])), observed=response_obs)

g = pm.model_to_graphviz(model)
g
../../../_images/c558f79388dc0da0b5198494f94fec094acab1801a6ca7c04bef8796b173e1a8.svg

推定#

%%time
with model:
    idata = pm.sample(random_seed=0, draws=1000)

Initializing NUTS using jitter+adapt_diag...

Multiprocess sampling (2 chains in 2 jobs)

NUTS: [a, b, theta]



---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
File <timed exec>:2

File ~/work/notes/notes/.venv/lib/python3.10/site-packages/pymc/sampling/mcmc.py:957, in sample(draws, tune, chains, cores, random_seed, progressbar, progressbar_theme, step, var_names, nuts_sampler, initvals, init, jitter_max_retries, n_init, trace, discard_tuned_samples, compute_convergence_checks, keep_warning_stat, return_inferencedata, idata_kwargs, nuts_sampler_kwargs, callback, mp_ctx, blas_cores, model, compile_kwargs, **kwargs)
    953 t_sampling = time.time() - t_start
    955 # Packaging, validating and returning the result was extracted
    956 # into a function to make it easier to test and refactor.
--> 957 return _sample_return(
    958     run=run,
    959     traces=trace if isinstance(trace, ZarrTrace) else traces,
    960     tune=tune,
    961     t_sampling=t_sampling,
    962     discard_tuned_samples=discard_tuned_samples,
    963     compute_convergence_checks=compute_convergence_checks,
    964     return_inferencedata=return_inferencedata,
    965     keep_warning_stat=keep_warning_stat,
    966     idata_kwargs=idata_kwargs or {},
    967     model=model,
    968 )

File ~/work/notes/notes/.venv/lib/python3.10/site-packages/pymc/sampling/mcmc.py:1042, in _sample_return(run, traces, tune, t_sampling, discard_tuned_samples, compute_convergence_checks, return_inferencedata, keep_warning_stat, idata_kwargs, model)
   1040 # Pick and slice chains to keep the maximum number of samples
   1041 if discard_tuned_samples:
-> 1042     traces, length = _choose_chains(traces, tune)
   1043 else:
   1044     traces, length = _choose_chains(traces, 0)

File ~/work/notes/notes/.venv/lib/python3.10/site-packages/pymc/backends/base.py:624, in _choose_chains(traces, tune)
    622 lengths = [max(0, len(trace) - tune) for trace in traces]
    623 if not sum(lengths):
--> 624     raise ValueError("Not enough samples to build a trace.")
    626 idxs = np.argsort(lengths)
    627 l_sort = np.array(lengths)[idxs]

ValueError: Not enough samples to build a trace.













EAP推定量#






post_mean = idata.posterior.mean(dim=["chain", "draw"])

# 項目パラメータのEAP推定量
params_EAP = pd.DataFrame({
    "item": coords["item"],
    "a": post_mean["a"],
    "b": post_mean["b"],
})
params_EAP.head()













  
    

      
      item
      a
      b
    

  
  
    

      0
      question_1
      1.026006
      0.351814
    

    

      1
      question_2
      0.995702
      0.360068
    

    

      2
      question_3
      0.674935
      0.582219
    

    

      3
      question_4
      1.062443
      0.673847
    

    

      4
      question_5
      0.993870
      -2.049681
    

  













Hide code cell source





fig, axes = plt.subplots(figsize=[12,4], ncols=3)

ax = axes[0]
ax.scatter(data["theta"], post_mean["theta"])
ax.plot(data["theta"], data["theta"], color="gray")
_ = ax.set(xlabel="true_theta", ylabel="theta_hat")

ax = axes[1]
ax.scatter(data["a"], post_mean["a"])
ax.plot(data["a"], data["a"], color="gray")
_ = ax.set(xlabel="true_a", ylabel="a_hat")

ax = axes[2]
ax.plot(data["b"], data["b"], color="gray")
ax.scatter(data["b"], post_mean["b"])
_ = ax.set(xlabel="true_b", ylabel="b_hat")










../../../_images/9147b80ec04bedce09c76817e5d34d268e81185209e24f2a7789de21b02d5572.png











    
    

                

              

              
              
              
              
                
              
            

            
            
              
                



  

  

     Contents