メトロポリス・ヘイスティング（MH）法#
Metropolis–Hastings（MH）は、比較的単純な MCMC（Markov Chain Monte Carlo） アルゴリズム。
基本アイデア
現在の状態 \(\theta\) から 提案分布（proposal） \(q(\theta' \mid \theta)\) により候補 \(\theta'\) を生成
\(\theta'\) を 確率的に受理 or 棄却
この操作を繰り返すことで、極限的に \(p(\theta \mid y)\) に従うマルコフ連鎖を得る
Metropolis–Hastings アルゴリズム
1. 初期化
初期値 \(\theta^{(0)}\) を適当に選ぶ。
\(t = 1, \dots, T\)について以下を繰り返す：
2. 提案ステップ
現在の状態 \(\theta^{(t)}\) の提案分布 \(q(\theta' \mid \theta^{(t)})\) から乱数を生成：
\[
\theta' \sim q(\theta' \mid \theta^{(t)})
\]
例：ランダムウォーク提案 \(\theta' = \theta^{(t)} + \varepsilon,\quad \varepsilon \sim \mathcal{N}(0, s^2)\)
3. 受理確率の計算
受理確率 \(r(\theta^{(t)}, \theta')\) を
\[
r(\theta^{(t)}, \theta')
=
\min\left(
1,\;
\frac{
p(\theta' \mid y)\, q(\theta^{(t)} \mid \theta')
}{
p(\theta^{(t)} \mid y)\, q(\theta' \mid \theta^{(t)})
}
\right)
\]
と定義する。
※事後分布の定義 \(p(\theta \mid y) \propto p(y \mid \theta)\, p(\theta)\) を代入すると
\[
r
=
\min\left(
1,\;
\frac{
p(y \mid \theta')\, p(\theta')\, q(\theta^{(t)} \mid \theta')
}{
p(y \mid \theta^{(t)})\, p(\theta^{(t)})\, q(\theta' \mid \theta^{(t)})
}
\right)
\]
ここで正規化定数は完全に相殺される。
4. 確率\(r\)で受理or棄却
一様乱数 \(u \sim \mathrm{Uniform}(0,1)\) を生成し、
\(u < r\) なら 受理： \(\theta^{(t+1)} = \theta'\)
それ以外は 棄却： \(\theta^{(t+1)} = \theta^{(t)}\)
"""
Metropolis-Hastings
- モデル: y_i ~ Normal(mu, sigma^2), 既知sigma
- 事前: mu ~ Normal(0, tau^2)
→ 事後 p(mu|y) を MCMC でサンプリング
ポイント:
- 正規化定数は不要（log事後の差だけ使う）
- 受理率(acceptance rate)と提案分布幅(step)で挙動が変わる
"""
import numpy as np
import matplotlib.pyplot as plt
# -----------------------------
# 1) データ生成（学習用に真値から作る）
# -----------------------------
rng = np.random.default_rng(0)
mu_true = 1.5
sigma = 1.0
n = 50
y = rng.normal(loc=mu_true, scale=sigma, size=n)
# 事前（mu ~ N(0, tau^2)）
tau = 3.0
# -----------------------------
# 2) log事後（正規化定数は捨ててOK）
# log p(mu|y) = log p(y|mu) + log p(mu) + const
# -----------------------------
def log_posterior(mu: float, y: np.ndarray, sigma: float, tau: float) -> float:
# log likelihood: sum_i log N(y_i | mu, sigma^2)
# 定数項 -0.5*log(2πσ^2) は差分で消えるので省略して良い
ll = -0.5 * np.sum(((y - mu) / sigma) ** 2)
# log prior: log N(mu | 0, tau^2) も定数は省略して良い
lp = -0.5 * ((mu / tau) ** 2)
return ll + lp
# -----------------------------
# 3) Metropolis-Hastings（ランダムウォーク提案）
# mu' = mu + Normal(0, step^2)
# -----------------------------
def metropolis_hastings(
y: np.ndarray,
sigma: float,
tau: float,
n_samples: int = 20_000,
burn_in: int = 2_000,
step: float = 0.5,
init: float = 0.0,
seed: int = 123,
):
rng = np.random.default_rng(seed)
samples = np.empty(n_samples, dtype=float)
mu = float(init)
logp = log_posterior(mu, y, sigma, tau)
accepted = 0
for t in range(n_samples):
# 提案
mu_prop = mu + rng.normal(0.0, step)
logp_prop = log_posterior(mu_prop, y, sigma, tau)
# 受理確率: alpha = min(1, exp(logp_prop - logp))
# 数値安定のため、log空間で比較する
log_alpha = logp_prop - logp
if np.log(rng.random()) < log_alpha:
mu = mu_prop
logp = logp_prop
accepted += 1
samples[t] = mu
acc_rate = accepted / n_samples
# burn-in を捨てて返す
post = samples[burn_in:]
return post, samples, acc_rate
# -----------------------------
# 4) 実行
# -----------------------------
post, trace, acc_rate = metropolis_hastings(
y=y,
sigma=sigma,
tau=tau,
n_samples=30_000,
burn_in=3_000,
step=0.6, # ←ここを変えると挙動が変わる（重要）
init=0.0,
seed=42,
)
print(f"acceptance rate = {acc_rate:.3f}")
print(f"posterior mean = {post.mean():.3f}")
print(f"posterior sd = {post.std(ddof=1):.3f}")
# -----------------------------
# 5) 可視化（トレース & ヒストグラム）
# -----------------------------
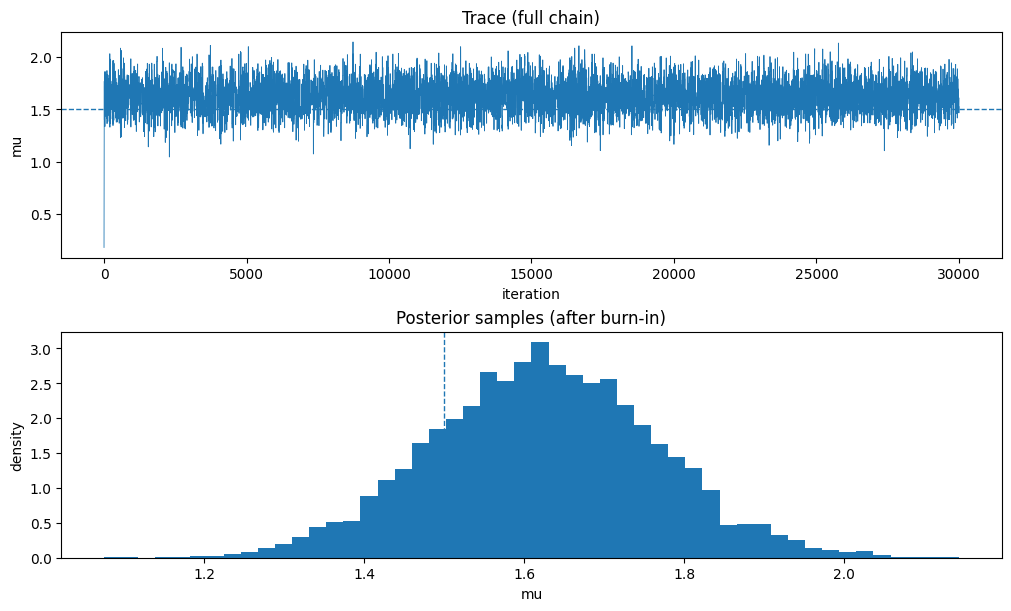
fig, ax = plt.subplots(2, 1, figsize=(10, 6), constrained_layout=True)
ax[0].plot(trace, linewidth=0.6)
ax[0].axhline(mu_true, linestyle="--", linewidth=1.0)
ax[0].set_title("Trace (full chain)")
ax[0].set_xlabel("iteration")
ax[0].set_ylabel("mu")
ax[1].hist(post, bins=50, density=True)
ax[1].axvline(mu_true, linestyle="--", linewidth=1.0)
ax[1].set_title("Posterior samples (after burn-in)")
ax[1].set_xlabel("mu")
ax[1].set_ylabel("density")
plt.show()
acceptance rate = 0.279
posterior mean = 1.624
posterior sd = 0.140
