t分布#
概要#
t分布（Student’s t-distribution）は、正規母集団からの小標本に基づく推測に用いられる連続確率分布である。正規分布に似た釣鐘型の形状をもつが、裾が重い（heavy-tailed）のが特徴である。
William Sealy Gosset が「Student」というペンネームで発表したことに由来する。自由度が大きくなるにつれて標準正規分布に近づく。
確率密度関数#
\(Z \sim N(0,1)\)と\(W \sim \chi^2_{(n)}\)が独立のとき、
\[
T = \frac{Z}{\sqrt{W/n}}
\]
は自由度\(n\)のt分布に従う。その確率密度関数は
\[
f(x \mid n) = \frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{n\pi}\,\Gamma\left(\frac{n}{2}\right)} \left(1 + \frac{x^2}{n}\right)^{-\frac{n+1}{2}}, \quad -\infty < x < \infty
\]
\(n\): 自由度（degrees of freedom, 正の整数）
累積分布関数#
\[
F(x) = \frac{1}{2} + x \frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{n\pi}\,\Gamma\left(\frac{n}{2}\right)} {}_2F_1\left(\frac{1}{2}, \frac{n+1}{2}; \frac{3}{2}; -\frac{x^2}{n}\right)
\]
ここで\({}_2F_1\)はガウスの超幾何関数である。閉じた簡潔な形では表せない。
期待値・分散#
\[
E[X] = 0 \quad (n > 1)
\]
\[
V[X] = \frac{n}{n-2} \quad (n > 2)
\]
\(n \leq 1\)のとき期待値は存在せず、\(n \leq 2\)のとき分散は存在しない（無限大）。自由度が大きくなると分散は\(1\)に近づき、標準正規分布の分散に一致する。
図#
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import t, norm
x = np.linspace(-5, 5, 300)
fig, axes = plt.subplots(1, 2, figsize=[8, 3])
for df in [1, 3, 10, 30]:
axes[0].plot(x, t.pdf(x, df=df), label=f"df={df}")
axes[1].plot(x, t.cdf(x, df=df), label=f"df={df}")
axes[0].plot(x, norm.pdf(x), 'k--', label=r"$N(0,1)$", alpha=0.7)
axes[1].plot(x, norm.cdf(x), 'k--', label=r"$N(0,1)$", alpha=0.7)
axes[0].set(title="PDF", xlabel="x", ylabel="f(x)")
axes[0].legend(fontsize=8)
axes[1].set(title="CDF", xlabel="x", ylabel="F(x)")
axes[1].legend(fontsize=8)
fig.tight_layout()
fig.show()
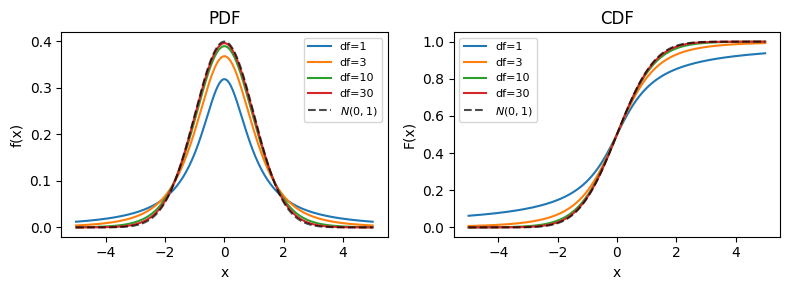
性質#
\(x=0\)に関して対称な分布である
\(n \to \infty\)で標準正規分布\(N(0,1)\)に収束する
\(n=1\)のときコーシー分布に一致する（期待値・分散が存在しない）
正規分布よりも裾が重く、外れ値に対してロバスト
正規母集団\(N(\mu, \sigma^2)\)からの標本平均\(\bar{X}\)と標本分散\(S^2\)を用いると、\(\frac{\bar{X}-\mu}{S/\sqrt{n}} \sim t_{(n-1)}\)
応用例#
t検定: 母平均に関する仮説検定（1標本t検定、2標本t検定、対応のあるt検定）
母平均の信頼区間の構成（母分散未知の場合）
回帰係数の有意性検定
ベイズ統計における裾の重い事前分布としての利用