二項分布

二項分布#

概要#

ベルヌーイ試行を独立に\(n\)回行ったときの「成功」の回数の分布。最も基本的な離散確率分布の一つであり、品質管理、医学統計、マーケティングなど幅広い分野で利用される。

確率質量関数#

\[ P(X=k \mid n, p) = \binom{n}{k} p^k (1-p)^{n-k}, \quad k=0,1,\dots,n \]

パラメータ:

  • \(n\): 試行回数（自然数）

  • \(p\): 各試行での成功確率 (\(0 \leq p \leq 1\))

  • \(\binom{n}{k} = \frac{n!}{k!(n-k)!}\): 二項係数

導出#

\(i=1,2,\dots,n\)に対して確率変数\(X_i\)を成功のとき1、失敗のとき0をとるものとすると、「成功」の回数は\(Y=\sum^n_{i=1}X_i\)と表すことができる。

\(Y=k\)となる確率は以下のようになる。

\[ P(Y=k) = \binom{n}{k} p^k (1 - p)^{n-k} \]

例：\(Y=2\)となる確率の場合

成功が2回、失敗が\(n-2\)回とする。

「成功」の事象を\(A_i\)、「失敗」の事象を\(A_i^c\)とすると、最初の2回が「成功」となる事象の確率は

\[ P(A_1 \cap A_2 \cap A_3^c \cap \cdots \cap A_n^c) \]

と表すことができる。

試行の独立性と\(P(A_i)=p, P(A_i^c)=1-p\)から

\[\begin{split} \begin{align} &P(A_1 \cap A_2 \cap A_3^c \cap \cdots \cap A_n^c)\\ &= P(A_1)P(A_2)P(A_3^c)\times\cdots\times P(A_n^c)\\ &= p^2(1-p)^{n-2} \end{align} \end{split}\]

と書くことができる。

\(n\)回試行して2回成功する事象の組み合わせは\(A_1 \cap A_2^c \cap A_3 \cap \cdots \cap A_n^c\)や\(A_1^c \cap A_2^c \cap A_3 \cap \cdots \cap A_n\)など他にも考えられ、その場合の数は組み合わせの数になるため\(\binom{n}{2}\)となる。

したがって、\(Y=2\)となる確率は

\[ P(Y=2) = \binom{n}{2} p^2 (1 - p)^{n-2} \]

となり、この\(2\)を\(k\)にすれば上記のものになる。

累積分布関数#

\[ F(k) = P(X \leq k) = \sum_{i=0}^{k} \binom{n}{i} p^i (1-p)^{n-i} \]

二項分布の累積分布関数には閉じた形の式は存在しない。正則化不完全ベータ関数を用いて

\[ F(k; n, p) = I_{1-p}(n - k, k + 1) \]

と表すこともできる。

期待値・分散#

\[ E[X] = np \]
\[ V[X] = np(1-p) \]

導出#

\(X = \sum_{i=1}^n X_i\) （\(X_i \sim \text{Bernoulli}(p)\)が互いに独立）と表せることを利用する。

ベルヌーイ分布の期待値は\(E[X_i] = p\)、分散は\(V[X_i] = p(1-p)\)であるから、期待値の線形性より

\[ E[X] = E\left[\sum_{i=1}^n X_i\right] = \sum_{i=1}^n E[X_i] = np \]

\(X_i\)が互いに独立であるため、分散についても

\[ V[X] = V\left[\sum_{i=1}^n X_i\right] = \sum_{i=1}^n V[X_i] = np(1-p) \]

が成り立つ。

Hide code cell source

 
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import binom

fig, axes = plt.subplots(1, 2, figsize=[8, 3])

# PMF
params = [(10, 0.3), (10, 0.5), (10, 0.7), (20, 0.5)]
for n, p in params:
    k = np.arange(0, n + 1)
    pmf = binom.pmf(k, n=n, p=p)
    axes[0].plot(k, pmf, 'o-', markersize=4, label=f"n={n}, p={p}")

axes[0].set(title="PMF", xlabel="k", ylabel="P(X=k)")
axes[0].legend()

# CDF
for n, p in params:
    k = np.arange(0, n + 1)
    cdf = binom.cdf(k, n=n, p=p)
    axes[1].step(k, cdf, where='mid', label=f"n={n}, p={p}")

axes[1].set(title="CDF", xlabel="k", ylabel="F(k)")
axes[1].legend()
fig.tight_layout()
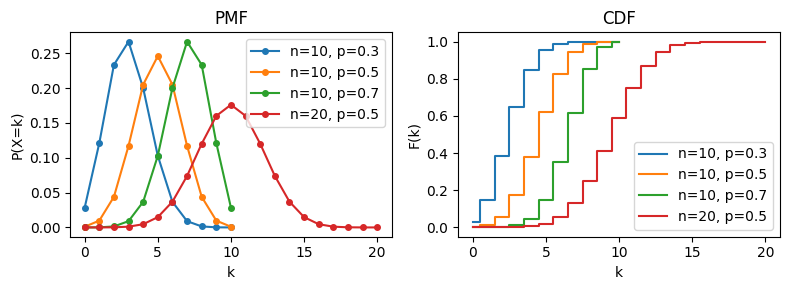
../../../_images/495260fc42470df188b1cb6d7acb1830bfd416fc869aa9df3fedccdfc368b212.png

性質#

  • \(n=1\)のときベルヌーイ分布に一致

  • 再生性：\(X_1 \sim B(n_1, p), X_2 \sim B(n_2, p)\)が独立なら\(X_1+X_2 \sim B(n_1+n_2, p)\)

  • \(n\)が大きく\(p\)が小さいとき、ポアソン分布\(\text{Poi}(np)\)で近似可（ポアソンの小数の法則）

  • \(np\)と\(n(1-p)\)がともに十分大きいとき、正規分布\(N(np, np(1-p))\)で近似可（中心極限定理）

  • 最頻値は\(\lfloor (n+1)p \rfloor\)または\(\lfloor (n+1)p \rfloor - 1\)

応用例#

  • 品質管理における不良品数のモデリング

  • 臨床試験における治療成功数

  • A/Bテストでのコンバージョン数

  • 選挙における得票数の予測

参考文献#

Contents