IRTモデルの識別性

IRTモデルの識別性#

項目反応理論（IRT）モデルでは、能力パラメータ\(\theta\)と項目パラメータ（\(a, b\)など）を同時に推定する。しかし、何らかの制約を課さなければパラメータが一意に定まらない 識別性（identifiability） の問題がある。

識別性の問題とは#

識別性（identifiability） とは、観測データからモデルのパラメータを一意に決定できるかどうかという性質である。

IRTモデルでは、2パラメータロジスティックモデル（2PLM）を例にとると

\[ P(u_{ij} = 1 \mid \theta_i, a_j, b_j) = \frac{1}{1 + \exp(-a_j(\theta_i - b_j))} \]

というモデルを考える。このとき、能力パラメータ\(\theta\)と項目パラメータ\((a, b)\)の間には本質的な不定性が存在する。

位置の不定性（Location Indeterminacy）#

能力パラメータ\(\theta\)と困難度パラメータ\(b\)に同じ定数\(c\)を加えても、モデルの予測確率は変わらない。

\[ a_j(\theta_i - b_j) = a_j((\theta_i + c) - (b_j + c)) \]

つまり、\((\theta, b)\)と\((\theta + c, b + c)\)は観測データに対して同じ尤度を与える。これを 位置の不定性 という。

直感的には「全員の能力を10点ずつ上げて、全問題の難易度も10点ずつ上げても、正答確率は変わらない」ということである。

尺度の不定性（Scale Indeterminacy）#

能力パラメータ\(\theta\)と困難度パラメータ\(b\)を同じ正の定数\(k > 0\)で割り、識別力パラメータ\(a\)を\(k\)倍しても、モデルの予測確率は変わらない。

\[ a_j(\theta_i - b_j) = (k \cdot a_j)\left(\frac{\theta_i}{k} - \frac{b_j}{k}\right) \]

つまり、\((a, \theta, b)\)と\((ka, \theta/k, b/k)\)は観測データに対して同じ尤度を与える。これを 尺度の不定性 という。

直感的には「能力と難易度の単位を変えても（例：点数からパーセントに変換）、識別力を適切に調整すれば正答確率は変わらない」ということである。

識別性の確保#

識別性の問題を解決するためには、パラメータに制約を課す必要がある。主に2つのアプローチがある。

  1. 能力パラメータへの制約：能力\(\theta\)の分布を固定する

  2. 項目パラメータへの制約：特定の項目のパラメータを固定する

能力パラメータへの制約#

最も一般的な方法は、能力パラメータ\(\theta\)が標準正規分布に従うと仮定することである。

\[ \theta_i \sim \mathcal{N}(0, 1) \]

この制約により：

  • 位置の不定性の解消：\(\mathrm{E}[\theta] = 0\)と固定することで、\(\theta\)と\(b\)に任意の定数を加える自由度がなくなる

  • 尺度の不定性の解消：\(\mathrm{Var}[\theta] = 1\)と固定することで、\(\theta\)と\(b\)を任意の定数で割る自由度がなくなる

この制約は周辺最尤推定法（MML）やベイズ推定で自然に導入される。

項目パラメータへの制約#

別のアプローチとして、特定の項目パラメータを固定する方法がある。

例えば：

  • 1つの項目の困難度を固定：\(b_1 = 0\)（位置の不定性を解消）

  • 1つの項目の識別力を固定：\(a_1 = 1\)（尺度の不定性を解消）

または、複数の項目パラメータの平均や分散を固定する方法もある：

  • \(\frac{1}{J}\sum_{j=1}^{J} b_j = 0\)（困難度の平均を0に固定）

  • \(\frac{1}{J}\sum_{j=1}^{J} a_j = 1\)（識別力の平均を1に固定）

この方法は同時最尤推定法（JML）でよく用いられる。

シミュレーション：識別性の問題の確認#

識別性の問題を具体的に確認するため、同じデータに対して異なるパラメータが同じ尤度を与えることを示す。

import numpy as np

def icc_2pl(theta, a, b):
    """2PLモデルのICC（項目特性曲線）"""
    return 1 / (1 + np.exp(-a * (theta - b)))

def log_likelihood(responses, theta, a, b):
    """対数尤度の計算"""
    prob = icc_2pl(theta[:, None], a, b)
    ll = np.sum(responses * np.log(prob + 1e-10) + (1 - responses) * np.log(1 - prob + 1e-10))
    return ll

# 真のパラメータ
np.random.seed(42)
n_persons, n_items = 100, 5
theta_true = np.random.normal(0, 1, n_persons)
a_true = np.array([1.0, 1.2, 0.8, 1.5, 1.1])
b_true = np.array([-1.0, -0.5, 0.0, 0.5, 1.0])

# データ生成
prob = icc_2pl(theta_true[:, None], a_true, b_true)
responses = np.random.binomial(1, prob)

# 真のパラメータでの対数尤度
ll_true = log_likelihood(responses, theta_true, a_true, b_true)
print(f"真のパラメータでの対数尤度: {ll_true:.4f}")

真のパラメータでの対数尤度: -278.3950

位置の不定性の確認#

# 位置の不定性：θとbに同じ定数cを加える
c = 5.0  # 任意の定数
theta_shifted = theta_true + c
b_shifted = b_true + c

ll_shifted = log_likelihood(responses, theta_shifted, a_true, b_shifted)
print(f"位置をシフトしたパラメータでの対数尤度: {ll_shifted:.4f}")
print(f"差: {abs(ll_true - ll_shifted):.10f}")

位置をシフトしたパラメータでの対数尤度: -278.3950
差: 0.0000000000

尺度の不定性の確認#

# 尺度の不定性：θとbをkで割り、aをk倍する
k = 2.0  # 任意の正の定数
theta_scaled = theta_true / k
b_scaled = b_true / k
a_scaled = a_true * k

ll_scaled = log_likelihood(responses, theta_scaled, a_scaled, b_scaled)
print(f"尺度を変換したパラメータでの対数尤度: {ll_scaled:.4f}")
print(f"差: {abs(ll_true - ll_scaled):.10f}")

尺度を変換したパラメータでの対数尤度: -278.3950
差: 0.0000000000

上記のように、異なるパラメータの組み合わせが全く同じ対数尤度を与えることが確認できた。これが識別性の問題である。

視覚的な確認#

異なるパラメータ化でも、正答確率（ICC）は同じになることを確認する。

Hide code cell source

 
import matplotlib.pyplot as plt

# 項目1のICCを比較
theta_range = np.linspace(-4, 4, 100)
j = 0  # 項目1

# 真のパラメータでのICC
icc_true = icc_2pl(theta_range, a_true[j], b_true[j])

# 位置シフトしたパラメータでのICC（θも調整が必要）
icc_shifted = icc_2pl(theta_range + c, a_true[j], b_shifted[j])

# 尺度変換したパラメータでのICC（θも調整が必要）
icc_scaled = icc_2pl(theta_range / k, a_scaled[j], b_scaled[j])

fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(theta_range, icc_true, 'b-', linewidth=2, label='Original')
ax.plot(theta_range, icc_shifted, 'r--', linewidth=2, label=f'Location shift (c={c})')
ax.plot(theta_range, icc_scaled, 'g:', linewidth=2, label=f'Scale transform (k={k})')
ax.set(xlabel=r'$\theta$ (original scale)', ylabel=r'$P(u=1)$', title='Item 1: ICC under different parameterizations')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()
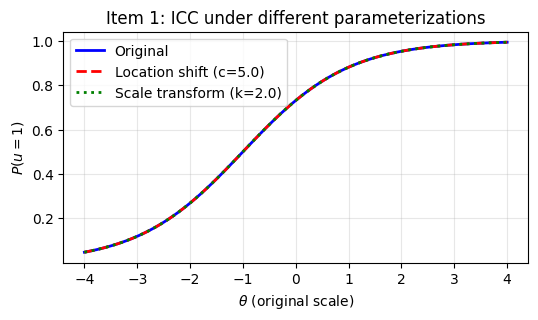
../../_images/8bc47d02a350ac27e90d404a9f2a3c15b4133ca5592f03971e704cefaee0283a.png

3つの曲線が完全に重なっており、異なるパラメータ化が同じ正答確率を生成することが確認できる。

ベイズ推定における識別性#

ベイズ推定では、事前分布を通じて識別性を確保することが自然にできる。

標準的な事前分布の設定#

\[\begin{split} \begin{aligned} \theta_i &\sim \mathcal{N}(0, 1) \\ a_j &\sim \text{LogNormal}(0, \sigma_a^2) \quad \text{or} \quad a_j \sim \text{HalfNormal}(\sigma_a) \\ b_j &\sim \mathcal{N}(0, \sigma_b^2) \end{aligned} \end{split}\]

  • \(\theta \sim \mathcal{N}(0, 1)\)：位置と尺度の両方を固定

  • \(a_j > 0\)の制約：識別力は正であるべき（負だとICCの傾きが反転する）

  • \(b_j\)には緩い正規分布：困難度の範囲を緩やかに制限

1PLモデル（Raschモデル）の識別性#

1PLモデルでは識別力\(a\)がすべての項目で共通（通常\(a=1\)と固定）であるため、尺度の不定性は最初から存在しない。

\[ P(u_{ij} = 1 \mid \theta_i, b_j) = \frac{1}{1 + \exp(-(\theta_i - b_j))} \]

この場合、位置の不定性のみを解消すればよく、以下のいずれかの制約を課す：

  • \(\sum_{i=1}^{I} \theta_i = 0\)（能力の総和を0に固定）

  • \(\sum_{j=1}^{J} b_j = 0\)（困難度の総和を0に固定）

  • \(\theta \sim \mathcal{N}(0, \sigma^2)\)（能力の平均を0に固定）

まとめ#

不定性の種類

変換

解消方法

位置の不定性

\((\theta, b) \to (\theta + c, b + c)\)

\(\mathrm{E}[\theta] = 0\) または \(\sum b_j = 0\)

尺度の不定性

\((\theta, a, b) \to (\theta/k, ka, b/k)\)

\(\mathrm{Var}[\theta] = 1\) または \(a_1 = 1\)

IRTモデルの推定では、これらの制約を意識することが重要である。特に：

  1. 使用するソフトウェアがどの制約を採用しているか確認する

  2. 異なる研究間でパラメータを比較する際は尺度を揃える

  3. ベイズ推定では事前分布を通じて自然に識別性を確保できる

参考文献#

Contents