負の二項分布

負の二項分布#

概要#

負の二項分布（negative binomial distribution）は、独立なベルヌーイ試行において\(r\)回目の成功が起こるまでの失敗回数の分布である。幾何分布の一般化であり、\(r=1\)のとき幾何分布に一致する。

ポアソン分布では期待値と分散が等しいという制約があるが、負の二項分布はこの制約がなく**過分散（overdispersion）**を扱えるため、カウントデータの分析において重要な代替モデルとなる。

確率質量関数#

\[ P(X=k \mid r, p) = \binom{k+r-1}{k} p^r (1-p)^k, \quad k=0,1,2,\dots \]

  • \(r > 0\): 成功回数（自然数。一般化する場合は正の実数）

  • \(p\): 各試行での成功確率 (\(0 < p \leq 1\))

\(r\)が正の実数の場合、二項係数は次のように一般化される：

\[ \binom{k+r-1}{k} = \frac{\Gamma(k+r)}{k!\,\Gamma(r)} \]

累積分布関数#

\[ F(k) = P(X \leq k) = I_p(r, k+1) \]

ここで\(I_p\)は正則化不完全ベータ関数である。

期待値・分散#

\[ E[X] = \frac{r(1-p)}{p} \]
\[ V[X] = \frac{r(1-p)}{p^2} \]

分散は次のように書き直すことができる：

\[ V[X] = E[X] + \frac{(E[X])^2}{r} \]

すなわち\(V[X] > E[X]\)が常に成り立ち、ポアソン分布（\(V[X]=E[X]\)）に比べて過分散となる。\(r \to \infty\)のとき第2項が消え、ポアソン分布に近づく。

図#

Hide code cell source

 
import matplotlib.pyplot as plt
import matplotlib_fontja
import numpy as np
from scipy.stats import nbinom

fig, axes = plt.subplots(1, 2, figsize=[8, 3])

params = [(3, 0.3), (5, 0.5), (10, 0.5), (3, 0.8)]
for r, p in params:
    k = np.arange(0, 25)
    pmf = nbinom.pmf(k, n=r, p=p)
    axes[0].plot(k, pmf, 'o-', markersize=4, label=f"r={r}, p={p}")

    cdf = nbinom.cdf(k, n=r, p=p)
    axes[1].step(k, cdf, where='mid', label=f"r={r}, p={p}")

axes[0].set(title="PMF", xlabel=r"k（失敗回数）", ylabel="P(X=k)")
axes[0].legend()
axes[1].set(title="CDF", xlabel="k", ylabel="F(k)")
axes[1].legend()
fig.tight_layout()
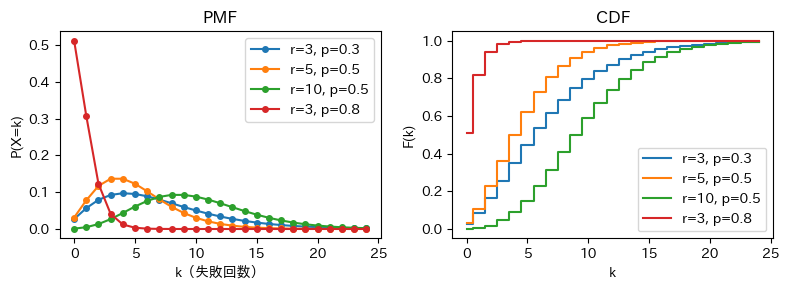
../../../_images/b427a1deebea7730b35937fc087b4e1f0f45d538ea49837015793ab776b812ff.png

性質#

  • \(r=1\)のとき幾何分布に一致する

  • 再生性: \(X_1 \sim \text{NB}(r_1, p), X_2 \sim \text{NB}(r_2, p)\)が独立なら\(X_1 + X_2 \sim \text{NB}(r_1+r_2, p)\)

  • ポアソン-ガンマ混合モデル: \(X \mid \lambda \sim \text{Poi}(\lambda)\)で\(\lambda \sim \text{Gamma}(r, (1-p)/p)\)のとき、\(X\)の周辺分布は\(\text{NB}(r, p)\)となる。この解釈により、負の二項分布は「発生率に個体差があるポアソン過程」とみなせる

  • \(r \to \infty\)で\(r(1-p)/p = \mu\)を一定に保つとポアソン分布\(\text{Poi}(\mu)\)に収束する

応用例#

  • 過分散のあるカウントデータの分析（ポアソン回帰の代替としての負の二項回帰）

  • 生態学における個体数のモデリング

  • RNA-seqデータにおける遺伝子発現量の分析（DESeq2等で使用）

  • 保険数理における事故件数のモデリング

Contents