ポアソン分布

ポアソン分布#

概要#

ポアソン分布（Poisson distribution）は、一定の時間・空間の中で稀に起こる事象の発生回数を表す離散確率分布である。

二項分布において試行回数\(n\)が大きく、成功確率\(p\)が小さい場合の極限として導出される（ポアソンの小数の法則）。事象の発生が互いに独立で、発生率が一定であるポアソン過程の基礎となる分布である。

確率質量関数#

\[ P(X=k \mid \lambda) = \frac{\lambda^k e^{-\lambda}}{k!}, \quad k=0,1,2,\dots \]

  • \(\lambda > 0\): 単位時間（空間）あたりの平均発生回数（rate parameter）

二項分布からの導出#

二項分布\(B(n,p)\)において\(n \to \infty, \ p \to 0\)かつ\(np = \lambda\)（一定）のとき：

\[ \binom{n}{k} p^k (1-p)^{n-k} = \frac{n!}{k!(n-k)!}\left(\frac{\lambda}{n}\right)^k\left(1-\frac{\lambda}{n}\right)^{n-k} \]
\[ = \frac{n(n-1)\cdots(n-k+1)}{n^k} \cdot \frac{\lambda^k}{k!} \cdot \left(1-\frac{\lambda}{n}\right)^{n} \cdot \left(1-\frac{\lambda}{n}\right)^{-k} \]

\(n \to \infty\)のとき、\(\frac{n(n-1)\cdots(n-k+1)}{n^k} \to 1\)、\(\left(1-\frac{\lambda}{n}\right)^{n} \to e^{-\lambda}\)、\(\left(1-\frac{\lambda}{n}\right)^{-k} \to 1\) であるから、

\[ \lim_{n\to\infty} \binom{n}{k} p^k (1-p)^{n-k} = \frac{\lambda^k e^{-\lambda}}{k!} \]

累積分布関数#

\[ F(k) = P(X \leq k) = e^{-\lambda} \sum_{i=0}^{k} \frac{\lambda^i}{i!} \]

閉じた形の表現はなく、正則化された上側不完全ガンマ関数を用いて

\[ F(k) = \frac{\Gamma(k+1, \lambda)}{k!} \]

と表すこともできる。

期待値・分散#

\[ E[X] = \lambda \]
\[ V[X] = \lambda \]

ポアソン分布の特徴的な性質として、期待値と分散が等しい（等分散性, equidispersion）。

期待値の導出

\[ E[X] = \sum_{k=0}^{\infty} k \cdot \frac{\lambda^k e^{-\lambda}}{k!} = \sum_{k=1}^{\infty} \frac{\lambda^k e^{-\lambda}}{(k-1)!} = \lambda e^{-\lambda} \sum_{k=1}^{\infty} \frac{\lambda^{k-1}}{(k-1)!} = \lambda e^{-\lambda} \cdot e^{\lambda} = \lambda \]

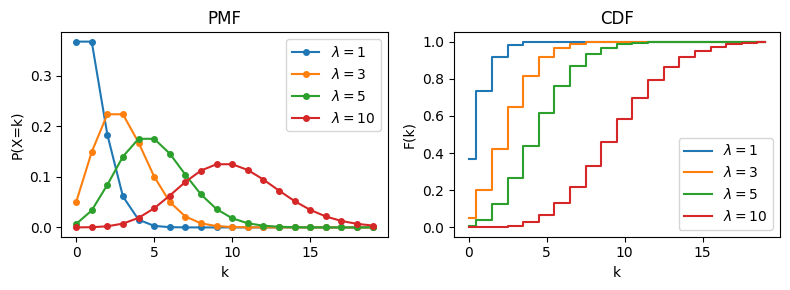
図#

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import poisson

fig, axes = plt.subplots(1, 2, figsize=[8, 3])

for lam in [1, 3, 5, 10]:
    k = np.arange(0, 20)
    pmf = poisson.pmf(k, mu=lam)
    axes[0].plot(k, pmf, 'o-', markersize=4, label=fr"$\lambda={lam}$")

    cdf = poisson.cdf(k, mu=lam)
    axes[1].step(k, cdf, where='mid', label=fr"$\lambda={lam}$")

axes[0].set(title="PMF", xlabel="k", ylabel="P(X=k)")
axes[0].legend()
axes[1].set(title="CDF", xlabel="k", ylabel="F(k)")
axes[1].legend()
fig.tight_layout()
fig.show()
../../../_images/759619d16d88ae764fcac242ae0ac1c613e0a11ff31454baf4623d133965f254.png

性質#

  • 再生性: \(X_1 \sim \text{Poi}(\lambda_1), X_2 \sim \text{Poi}(\lambda_2)\)が独立なら\(X_1 + X_2 \sim \text{Poi}(\lambda_1 + \lambda_2)\)

  • ポアソンの小数の法則: 二項分布\(B(n,p)\)で\(n\)が大きく\(p\)が小さいとき\(\text{Poi}(np)\)で近似可能

  • 正規近似: \(\lambda\)が大きいとき正規分布\(N(\lambda, \lambda)\)で近似可能（中心極限定理）

  • 指数型分布族に属する

  • 過分散（overdispersion）: 実データでは分散が期待値より大きいことが多く、その場合は負の二項分布が代替として用いられる

応用例#

  • 単位時間あたりのコールセンターへの着信回数

  • ウェブサイトへの単位時間あたりのアクセス数

  • 一定面積あたりの放射性崩壊の回数

  • 希少疾患の発症数のモデリング

  • ポアソン回帰（GLMの一種）によるカウントデータの分析

参考文献#

Contents