カイ二乗分布

カイ二乗分布#

概要#

カイ二乗分布（chi-squared distribution）は、標準正規分布に従う独立な確率変数の二乗和が従う分布である。統計的検定（適合度検定、独立性検定）や信頼区間の構成において中心的な役割を果たす。ガンマ分布の特殊ケースである。

確率密度関数#

標準正規分布に従う確率変数\(X_i\)の二乗和\(Z = \sum_{i=1}^n X_i^2\)は自由度\(n\)のカイ二乗分布に従う。

\[ Z \sim \chi^2_{(n)} \]

その確率密度関数は

\[ f(x \mid n) = \frac{1}{\Gamma(n/2)} \left( \frac{1}{2} \right)^{n/2} x^{n/2-1} \exp \left\{ - \frac{x}{2} \right\}, \quad x > 0 \]

  • \(n\): 自由度（degrees of freedom, 正の整数）

累積分布関数#

\[ F(x) = \frac{\gamma(n/2,\ x/2)}{\Gamma(n/2)} \]

ここで\(\gamma(s, x)\)は下側不完全ガンマ関数。閉じた形では表せない。

期待値・分散#

\[ E[X] = n \]
\[ V[X] = 2n \]

図#

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import chi2

x = np.linspace(0, 25, 200)

fig, axes = plt.subplots(1, 2, figsize=[8, 3])

for df in [1, 3, 5, 10]:
    pdf = chi2.pdf(x, df=df)
    axes[0].plot(x, pdf, label=f"df={df}")
    cdf = chi2.cdf(x, df=df)
    axes[1].plot(x, cdf, label=f"df={df}")

axes[0].set(title="PDF", xlabel="x", ylabel="f(x)")
axes[0].legend()
axes[1].set(title="CDF", xlabel="x", ylabel="F(x)")
axes[1].legend()
fig.tight_layout()
fig.show()
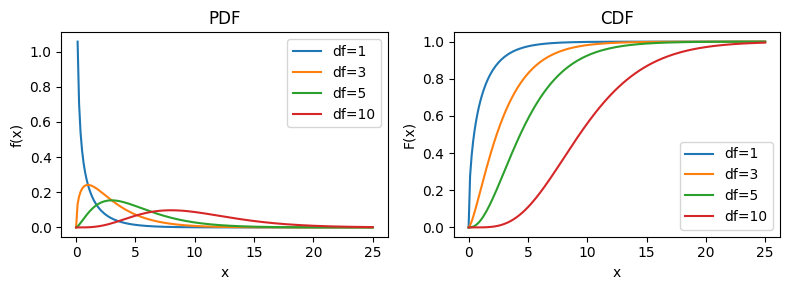
../../../_images/3ddc9664ad4e2828379f913a3ff17945a10945e44777ae34ce1c83fc27b222d3.png

性質#

  • ガンマ分布の特殊ケース: \(\chi^2_{(n)} = \text{Gamma}(n/2, 2)\)

  • 再生性: \(X_1 \sim \chi^2_{(n_1)}, X_2 \sim \chi^2_{(n_2)}\)が独立なら\(X_1 + X_2 \sim \chi^2_{(n_1+n_2)}\)

  • 自由度\(n\)が大きいとき、中心極限定理により\(\chi^2_{(n)}\)は近似的に\(N(n, 2n)\)に従う

  • 正規母集団\(N(\mu, \sigma^2)\)からの標本分散\(S^2\)に対して、\(\frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{(n-1)}\)

  • \(n=1\)のとき、\(\chi^2_{(1)}\)は標準正規分布の二乗と一致

  • \(n=2\)のとき、指数分布\(\text{Exp}(1/2)\)と一致

応用例#

  • カイ二乗適合度検定: 観測度数と期待度数の乖離の検定

  • カイ二乗独立性検定: 分割表における2変数の独立性の検定

  • 母分散に関する推測（信頼区間の構成、仮説検定）

  • 尤度比検定における漸近分布

参考文献#

Contents