正規分布

正規分布#

概要#

正規分布（normal distribution）は、統計学において最も重要な連続確率分布である。ガウス分布（Gaussian distribution）とも呼ばれる。

中心極限定理により、多数の独立な確率変数の和は（元の分布の形状によらず）正規分布に近づくため、自然現象や社会現象の多くが近似的に正規分布に従う。統計的推測の多くの手法は正規分布を前提として構築されている。

確率密度関数#

確率変数\(X\)が平均\(\mu\)、分散\(\sigma^2\)の正規分布に従うとは、\(X\)の確率密度関数が

\[ f(x \mid \mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma} \exp \left\{ - \frac{(x-\mu)^2}{2\sigma^2} \right\} , \quad -\infty < x < \infty \]

で与えられることをいい、この分布を\(N(\mu, \sigma^2)\)で表す。

  • \(\mu\): 平均（location parameter）

  • \(\sigma^2\): 分散（\(\sigma > 0\), scale parameter）

\(\mu=0, \sigma^2=1\)のとき標準正規分布\(N(0,1)\)と呼ぶ。

累積分布関数#

\[ F(x) = \Phi\left(\frac{x-\mu}{\sigma}\right) = \frac{1}{2}\left[1 + \text{erf}\left(\frac{x-\mu}{\sigma\sqrt{2}}\right)\right] \]

ここで\(\Phi\)は標準正規分布の累積分布関数、\(\text{erf}\)は誤差関数である。閉じた形の初等関数では表せない。

期待値・分散#

\[ E[X] = \mu \]
\[ V[X] = \sigma^2 \]

図#

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm

x = np.linspace(-6, 6, 300)

fig, axes = plt.subplots(1, 2, figsize=[8, 3])

params = [(0, 1), (0, 2), (0, 0.5), (2, 1)]
for mu, sigma in params:
    pdf = norm.pdf(x, loc=mu, scale=sigma)
    axes[0].plot(x, pdf, label=fr"$\mu={mu}, \sigma={sigma}$")
    cdf = norm.cdf(x, loc=mu, scale=sigma)
    axes[1].plot(x, cdf, label=fr"$\mu={mu}, \sigma={sigma}$")

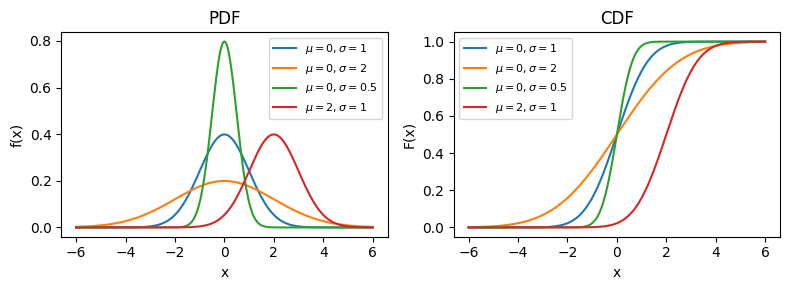
axes[0].set(title="PDF", xlabel="x", ylabel="f(x)")
axes[0].legend(fontsize=8)
axes[1].set(title="CDF", xlabel="x", ylabel="F(x)")
axes[1].legend(fontsize=8)
fig.tight_layout()
fig.show()
../../../_images/3d9cef17aabe6ceb4b5471ccb8cf0e77b177ffaeadc188bb9719da9ed5904dc3.png

性質#

  • \(\mu\)に関して対称な分布であり、平均=中央値=最頻値

  • 再生性: \(X_1 \sim N(\mu_1, \sigma_1^2), X_2 \sim N(\mu_2, \sigma_2^2)\)が独立なら\(X_1 + X_2 \sim N(\mu_1+\mu_2, \sigma_1^2+\sigma_2^2)\)

  • 最大エントロピー性: 平均と分散を固定したとき、エントロピーを最大にする連続分布は正規分布である

  • 中心極限定理: 独立同一分布に従う確率変数の標準化された和は、元の分布に関わらず正規分布に収束する

  • 線形変換: \(X \sim N(\mu, \sigma^2)\)のとき\(aX+b \sim N(a\mu+b, a^2\sigma^2)\)

  • 標準化: \(Z = \frac{X-\mu}{\sigma} \sim N(0,1)\)

  • 指数型分布族に属する

  • 68-95-99.7 ルール: データの約68%が\(\mu \pm \sigma\)に、約95%が\(\mu \pm 2\sigma\)に、約99.7%が\(\mu \pm 3\sigma\)に含まれる

応用例#

  • 測定誤差のモデリング

  • 統計的推測の基礎（t検定、信頼区間など）

  • 品質管理（管理図、工程能力指数）

  • 金融工学（ブラック-ショールズモデルにおけるリターンの分布）

  • 機械学習（ガウス過程、正規化など）

参考文献#

Contents