正規累積モデル

正規累積モデル（normal ogive model） は基本的なIRTの考え方を示すモデル。正規累積モデルは概念上のわかり易さがある一方で、計算量の問題もあり、伝統的にはロジスティック・シグモイド関数により近似したロジスティックモデルが活用されてきた。そのため実際のところ最も基本的なIRTモデルはロジスティックモデルだが、そのベースになるのが正規累積モデル。

モデルの考え方

\(i\)番目の被験者の\(j\)番目の項目の値\(y_{ij}\)が二値\(y_{ij}\in\{0, 1\}\)であるとする（例えば正解・不正解だったり、アンケートの「あてはまる」「あてはまらない」という2件法など）。

\(y_{ij}\)の背後には潜在的な能力の連続量\(\theta_i \in \mathbb{R}\)が存在し、\(\theta_i\)が閾値\(b_j\)を超えていたら1、超えていなければ0が観測されるとする。つまり\(y_{ij}\)が以下のように決まるとする。

\[\begin{split} y_{ij} = \begin{cases} 0 & \text{ if } \theta_i < b_j\\ 1 & \text{ if } \theta_i \geq b_j\\ \end{cases} \end{split}\]

しかし、実際には被験者\(i\)の体調や運（たまたま正解できた）などにより、常にこのようにきれいに正解・不正解が決まるわけではないと考えられる。こうした誤差を表すパラメータ\(\varepsilon_{ij} \sim N(0, \sigma^2_{\varepsilon})\)も追加して

\[\begin{split} y_{ij} = \begin{cases} 0 & \text{ if } (\theta_i - \varepsilon_{ij}) < b_j\\ 1 & \text{ if } (\theta_i - \varepsilon_{ij}) \geq b_j\\ \end{cases} \end{split}\]

とする。誤差が確率変数のため、\(y_{ij}\)のとる値も確率変数として考えることができるようになる。\(b_j\)を移項すると

\[\begin{split} y_{ij} = \begin{cases} 0 & \text{ if } (\theta_i - \varepsilon_{ij} - b_j) < 0\\ 1 & \text{ if } (\theta_i - \varepsilon_{ij} - b_j) \geq 0\\ \end{cases} \end{split}\]

となる。\(\theta_i - \varepsilon_{ij} - b_j \sim N(\theta_i - b_j, \sigma^2_{\varepsilon})\)である。 \(\varepsilon_{ij}\)を移項すれば

\[\begin{split} y_{ij} = \begin{cases} 0 & \text{ if } (\theta_i - b_j) < \varepsilon_{ij}\\ 1 & \text{ if } (\theta_i - b_j) \geq \varepsilon_{ij}\\ \end{cases} \end{split}\]

でもあるので「\(y_{ij}=1\)となるのは誤差\(\varepsilon_{ij}\)が\(\theta_i - b_j\)以下のとき」とわかる。

Show code cell source

Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
epsilon = np.linspace(-4, 4, 1000)
y = norm.pdf(epsilon)
fig, ax = plt.subplots(figsize=[4,2])
ax.plot(epsilon, y, 'k-')

c = 1

ax.fill_between(epsilon, y, where=(epsilon < c), color='blue', alpha=0.3, label=r'$P(y_{ij} = 1)$')
ax.fill_between(epsilon, y, where=(epsilon >= c), color='red', alpha=0.3, label=r'$P(y_{ij} = 0)$')
ax.axvline(x=c, color='grey', linestyle='--', label=r'$\theta_i - b_j$')
ax.set(
    title=r'$\varepsilon_{ij} \sim N(0, 1)$',
    xlabel=r"$\varepsilon_{ij}$",
    ylabel="density"
)
ax.legend()
ax.grid(True)
fig.show()

1パラメータ正規累積モデル

仮に\(\varepsilon_{ij}\)が標準正規分布（\(\sigma^2_{\varepsilon} = 1\)の正規分布）に従うならば、特性値\(\theta_i\)の人が項目\(j\)に当てはまると回答する確率は

\[\begin{split} \begin{aligned} P(y_{ij} = 1) &= P(\varepsilon_{ij} \leq \theta_i - b_j)\\ &= \int_{-\infty}^{\left(\theta_i-b_j\right)} \frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{z^2}{2}\right) d z \end{aligned} \end{split}\]

となる（最後のは、\(\varepsilon_{ij}\)が従う標準正規分布のうち \(-\infty\) から \(\theta_i-b_j\) までの範囲の面積が\(P(\varepsilon_{ij} \leq \theta_i - b_j)\)ということ）。

Show code cell source

Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
x = np.linspace(-4, 4, 1000)

fig, ax = plt.subplots(figsize=[4, 2], ncols=1)

def icc(x, a, b):
    return norm.cdf(x, loc=b, scale=1/a)

a = 1
for b in [-1, 0, 1]:
    ax.plot(x, icc(x, a, b), label=r"$b$ = " + f"{b}")
ax.set(xlabel=r"$\theta_i$", ylabel=r"$P(y_{ij} = 1)$", xticklabels=[], yticklabels=[])
ax.legend()
ax.grid(True)

2パラメータ正規累積モデル

\(\sigma^2_{\varepsilon}\)が項目ごとに異なる場合を考える。\(\sigma^2_{\varepsilon}=1/a_j\)とすると、誤差の確率分布は

\[ \varepsilon_{ij} \sim N\left(0, \frac{1}{a_j}\right) \]

となる。両辺を\(a_j\)倍すると、\(a_j \varepsilon_{ij} \sim N(0, 1)\)と表すことができ、引き続き標準正規分布を使うことができる。そのためモデルは\(a_i\)が追加され

\[\begin{split} \begin{aligned} P(y_{ij} = 1) &= P(a_j \varepsilon_{ij} \leq \theta_i - b_j)\\ &= \int_{-\infty}^{ a_j (\theta_i-b_j)} \frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{z^2}{2}\right) d z \end{aligned} \end{split}\]

となる。

パラメータの意味

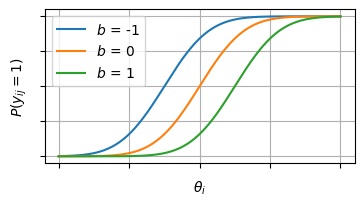
\(b_j\)が大きくなると\(\theta_i - b_j\)の値は小さくなり、\(P(y_{ij} = 1)\)の面積が小さくなる。\(y_{ij} = 1\)が正解を表しているとするなら、正答率が低くなる方向に作用する。そのため\(b_j\)は 項目困難度（item difficulty） と呼ばれる。

項目特性曲線（ICC）との関係でいうと、ICCが0.5になる点が\(b_j = \theta_i\)となる。つまり、困難度が高いほど正答率50%の点にくる\(\theta_i\)も高くなる

また\(a_j\)は値が大きくなると\(\varepsilon_{ij}\)の分散を下げて分布がより尖っていく。また横軸に\(\theta_i - b_j\)、縦軸に\(P(y_{ij} = 1)\)のグラフを書くとき、この曲線の傾きを急にして、\(\theta_i\)が低い人と高い人の間で\(P(y_{ij} = 1)\)の変化を大きくする。例えば、\(\theta_i\)のある点を境にして正解/不正解がはっきり分かれるデータならICCの傾きは急になり、\(a_j\)は高くなる。 そのため\(a_j\)は 項目識別力（item discrimination） と呼ばれる。

Show code cell source

Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
x = np.linspace(-4, 4, 1000)

fig, axes = plt.subplots(figsize=[8, 2], ncols=2)

def icc(x, a, b):
    return norm.cdf(x, loc=b, scale=1/a)

a = 1
for b in [-1, 0, 1]:
    axes[0].plot(x, icc(x, a, b), label=r"$b$ = " + f"{b}")
axes[0].set(xlabel=r"$\theta_i$", ylabel=r"$P(y_{ij} = 1)$", xticklabels=[], yticklabels=[])
axes[0].legend()
axes[0].grid(True)

b = 0
for a in [0.5, 1, 2]:
    axes[1].plot(x, icc(x, a, b), label=r"$a$ = " + f"{a}")
axes[1].set(xlabel=r"$\theta_i$", ylabel=r"$P(y_{ij} = 1)$", xticklabels=[], yticklabels=[])
axes[1].legend()
axes[1].grid(True)

なお横軸に\(\theta_i\)、縦軸に\(P(y_{ij}=1)\)をとったグラフは 項目特性曲線 （item characteristic curve: ICC） と呼ばれる。

因子分析との関係

因子分析と2P正規累積モデルは等価

因子分析と2パラメータ正規累積モデルは数学的に等価であると知られている。標準化していない（切片が0でない）1因子モデルは、切片\(\tau_j\)、因子負荷量\(a_j\)、因子スコア\(f_i\)で

\[ y_{ij} = \tau_j + a_j f_i - \varepsilon_{ij} \quad (\varepsilon_{ij}\sim N(0, \sigma_{\varepsilon})) \]

となる（IRTの説明に合わせて誤差の符号をマイナスにしている）

カテゴリカル因子分析では「離散的な観測変数\(y_{ij}\)はその背後にある潜在的な連続変数によって決まる」という考え方をするため、IRTの冒頭の説明と同じで

\[\begin{split} y_{ij} = \begin{cases} 0 & \text{ if } (\tau_j + a_j f_i) < \varepsilon_{ij}\\ 1 & \text{ if } (\tau_j + a_j f_i) \geq \varepsilon_{ij}\\ \end{cases} \end{split}\]

つまり標準正規分布に従う誤差\(\varepsilon_{ij}\)が\(\tau_j + a_j f_i\)より小さいときに\(y_{ij}=1\)となると考えるため、その確率\(P(y_{ij}=1)\)は

\[\begin{split} \begin{aligned} P(y_{ij} = 1) &= P(\varepsilon_{ij} \leq \tau_j + a_j f_i)\\ &= \int_{-\infty}^{ (\tau_j + a_j f_i)} \frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{z^2}{2}\right) d z \end{aligned} \end{split}\]

となる。2つのモデルのパラメータを\((f_i, a_j, \tau_j) = (\theta_i, a_j, a_j b_j)\)と対応させると

\[\begin{split} \begin{aligned} \tau_j + a_j f_i &= a_j \left( f_i + \frac{\tau_j}{a_j} \right) \\ &= a_j (\theta_i - b_i) \end{aligned} \end{split}\]

となる。