指数分布

指数分布#

概要#

指数分布（exponential distribution） は生存時間などを表すのに使われる分布。幾何分布の連続版であり、ポアソン過程における事象間の待ち時間を表す。離散確率分布における幾何分布と同様に、連続確率分布の中で唯一の無記憶性をもつ分布である。

確率密度関数#

\[ f(x \mid \lambda) = \lambda e^{-\lambda x}, \quad x > 0 \]

  • \(x\)：対象の変数（例：「商品が売れるまでの日数」、「製品が故障するまでの年数」）

  • \(\lambda > 0\)：rate parameter（発生率）

この分布を\(\text{Exp}(\lambda)\)と表記する。

累積分布関数#

\[ F(x) = P(X < x) = 1 - e^{-\lambda x} \]

例えば、「ある商品が\(x\)日で売れる確率」を \(\text{Exp}(\lambda) = \lambda e^{-\lambda x}\) とすると、累積分布関数 \(P(X < x) = 1- e^{-\lambda x}\) は「商品が\(x\)日未満で売れる確率」となる。

期待値・分散#

\[ E[X] = \frac{1}{\lambda} \]
\[ V[X] = \frac{1}{\lambda^2} \]

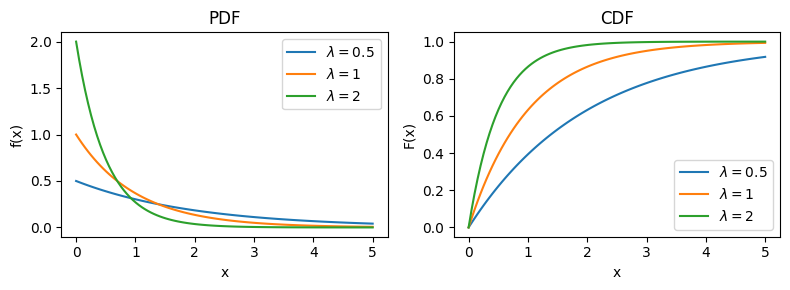
図#

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import expon

x = np.linspace(0, 5, 100)

fig, axes = plt.subplots(1, 2, figsize=[8, 3])

for lam in [0.5, 1, 2]:
    axes[0].plot(x, expon.pdf(x, scale=1/lam), label=fr"$\lambda={lam}$")
    axes[1].plot(x, expon.cdf(x, scale=1/lam), label=fr"$\lambda={lam}$")

axes[0].set(title="PDF", xlabel="x", ylabel="f(x)")
axes[0].legend()
axes[1].set(title="CDF", xlabel="x", ylabel="F(x)")
axes[1].legend()
fig.tight_layout()
fig.show()
../../../_images/e5a173b3e5d46e9bf936f472579097cd88da6ea2987cd331bd9115bd017f4e3f.png

ハザード関数#

\(X\)を非負の連続型確率変数とし、その密度関数を\(f(x)\)、分布関数を\(F(x)\)とする。\(X\)を生命が死亡したり機械が故障する時間を表す変数とみなすと、\(x\)時間まで生存していて次の時間\(x+\Delta\)までに死亡する条件付き確率は

\[\begin{split} \begin{aligned} P(x<X \leq x+\Delta \mid X>x) & =\frac{P(x<X \leq x+\Delta, X>x)}{P(X>x)} \\ & =\frac{P(x<X \leq x+\Delta)}{P(X>x)}\\ &=\frac{F(x+\Delta)-F(x)}{1-F(x)} \end{aligned} \end{split}\]

両辺を\(\Delta\)で割ると

\[\begin{split} \begin{aligned} \frac{1}{\Delta} P(x<X \leq x+\Delta \mid X>x) &=\frac{1}{\Delta} \cdot \frac{F(x+\Delta)-F(x)}{1-F(x)}\\ &=\frac{F(x+\Delta)-F(x)}{\Delta} \cdot \frac{1}{1-F(x)} \end{aligned} \end{split}\]

\(\Delta \to 0\)の極限を考えると、\(\frac{F(x+\Delta)-F(x)}{\Delta}\)は微分の定義と同じ形であるから、分布関数の微分すなわち確率密度関数である。

\[ \lim_{\Delta\downarrow 0} \frac{F(x+\Delta)-F(x)}{\Delta} = F'(x) = f(x) \]

なので

\[ \lim _{\Delta \downarrow 0} \frac{1}{\Delta} P(x<X \leq x+\Delta \mid X>x) = \frac{f(x)}{1-F(x)} \]

となる。

この「\(x\)時間まで生存していて次の時間\(x+\Delta\)までに死亡する条件付き確率」

\[ \lambda(x) = \frac{f(x)}{1-F(x)} \]

を ハザード関数 (hazard function) という。

指数分布のハザード関数#

ハザード関数に指数分布をあてはめると

\[ \lambda(x) = \frac{f(x)}{1-F(x)} = \frac{\lambda e^{-\lambda x}}{1 - (1- e^{-\lambda x})} = \frac{\lambda e^{-\lambda x}}{e^{-\lambda x}} = \lambda \]

であり、次の瞬間に死亡する確率密度は時間\(x\)に無関係で常に一定で\(\lambda\)となっていることがわかる（幾何分布や指数分布のこの性質は 無記憶性 と呼ばれる）。

ハザード関数による非負の連続型確率分布の生成#

非負の連続型確率変数の分布は、ハザード関数によって特徴づけられる。

ハザード関数の両辺を積分すると

\[ \int_0^x \lambda(t) d t = \int_0^x \frac{ f(t) }{ 1-F(t)} d t = [- \log (1 - F(t))]^x_0 \]

となる

途中式メモ

\(u=1-F(t)\) と置き換えると、 \(d u=-F^{\prime}(t) d t=-f(t) d t\) と置き換えられる。したがって

\[ \int_0^x \frac{f(t)}{1-F(t)} d t =\int_{t=0}^{t=x} - \frac{d u}{u} =\int_{t=0}^{t=x} - \frac{1}{u} d u \]

となる。\(-\frac{1}{u}\)の原始関数は\(-\log u\)なので

\[ \int_{t=0}^{t=x} - \frac{1}{u} d u = - \log u \]

\(u=1-F(t)\)を代入して戻せば

\[ \int_0^x \frac{f(t)}{1-F(t)} d t=[-\log (1-F(t))]_{t=0}^{t=x} \]

これは、次のように整理できる

\[\begin{split} \begin{aligned} & F(x)=1-\exp \left\{-\int_0^x \lambda(t) d t\right\} \\ & f(x)=\lambda(x) \exp \left\{-\int_0^x \lambda(t) d t\right\} \end{aligned} \end{split}\]
途中式

\(S(x):=1-F(x)\)とおく（これは 生存関数 と呼ばれる）。するとハザード関数は

\[ \lambda(x)=\frac{f(x)}{1-F(x)}=\frac{f(x)}{S(x)} \]

となる。ハザード関数の積分は、確率変数が非負なので\(F(0)=0 \implies S(0) = 1 \implies \log S(0) = 0\) なので、

\[\begin{split} \begin{aligned} \int_0^x \lambda(t) d t &=-[\log S(t)]_0^x\\ &= -\log S(x) + \log S(0)\\ &= -\log S(x) \end{aligned} \end{split}\]

となる。両辺を-1倍して指数をとれば

\[ S(x) = \exp \left\{ - \int_0^x \lambda(t) d t \right\} \]

となるので、ハザード関数は

\[\begin{split} \begin{aligned} \lambda(x) &= \frac{f(x)}{1 - F(x)} =\frac{f(x)}{S(x)}\\ &\iff \lambda(x) S(x) = f(x)\\ &\iff \boxed{ f(x) = \lambda(x) \exp \left\{ - \int_0^x \lambda(t) d t \right\} } \end{aligned} \end{split}\]

と整理でき、また

\[\begin{split} \begin{aligned} F(x) &= 1 - S(x) \\ &= \boxed{ 1-\exp \left\{-\int_0^x \lambda(t) d t\right\} } \end{aligned} \end{split}\]

例えば\(\lambda(x) = \lambda\)と定数をおくと指数分布が生ずる。

性質#

  • 無記憶性: \(P(X > s + t \mid X > s) = P(X > t)\)。連続確率分布の中で無記憶性を持つのは指数分布のみ

  • ガンマ分布\(\text{Gamma}(1, 1/\lambda)\)の特殊ケース

  • ポアソン過程における事象間の待ち時間は指数分布に従う

  • \(n\)個の独立な\(\text{Exp}(\lambda)\)の和はガンマ分布\(\text{Gamma}(n, 1/\lambda)\)に従う

  • ハザード関数が定数\(\lambda\)であることが指数分布を特徴づける

応用例#

  • 機器の故障までの時間（故障率が一定の場合）

  • 顧客が来店するまでの待ち時間

  • 放射性物質の崩壊までの時間

  • 生存分析における基本的な生存時間モデル

  • 待ち行列理論（M/M/1キューなど）

参考文献#

Contents