F分布

F分布#

概要#

F分布（F-distribution）は、2つの独立なカイ二乗分布に従う確率変数の比として定義される連続確率分布である。Ronald A. Fisher に因んで名付けられた。

分散の比較や回帰分析のモデル全体の有意性検定など、統計的推測において重要な役割を果たす。

確率密度関数#

\(U \sim \chi^2_{(d_1)}, V \sim \chi^2_{(d_2)}\)が独立のとき、

\[ F = \frac{U/d_1}{V/d_2} \]

は自由度\((d_1, d_2)\)のF分布に従う。その確率密度関数は

\[ f(x \mid d_1, d_2) = \frac{1}{B\left(\frac{d_1}{2}, \frac{d_2}{2}\right)} \left(\frac{d_1}{d_2}\right)^{d_1/2} x^{d_1/2-1} \left(1 + \frac{d_1}{d_2}x\right)^{-(d_1+d_2)/2}, \quad x > 0 \]

  • \(d_1\): 分子の自由度

  • \(d_2\): 分母の自由度

累積分布関数#

\[ F(x) = I_{\frac{d_1 x}{d_1 x + d_2}}\left(\frac{d_1}{2}, \frac{d_2}{2}\right) \]

ここで\(I_z(a,b)\)は正則化不完全ベータ関数である。

期待値・分散#

\[ E[X] = \frac{d_2}{d_2 - 2} \quad (d_2 > 2) \]
\[ V[X] = \frac{2 d_2^2 (d_1 + d_2 - 2)}{d_1 (d_2 - 2)^2 (d_2 - 4)} \quad (d_2 > 4) \]

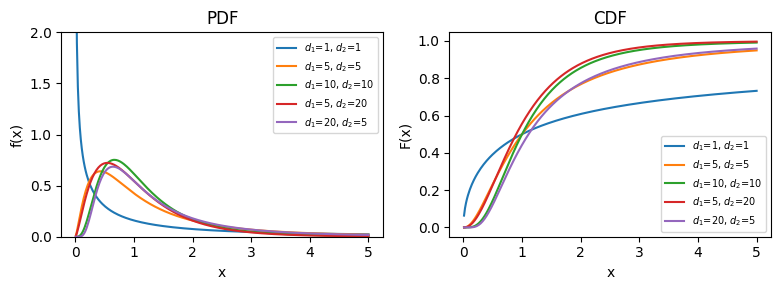
図#

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import f as f_dist

x = np.linspace(0.01, 5, 300)

fig, axes = plt.subplots(1, 2, figsize=[8, 3])

params = [(1, 1), (5, 5), (10, 10), (5, 20), (20, 5)]
for d1, d2 in params:
    pdf = f_dist.pdf(x, dfn=d1, dfd=d2)
    axes[0].plot(x, pdf, label=f"$d_1$={d1}, $d_2$={d2}")
    cdf = f_dist.cdf(x, dfn=d1, dfd=d2)
    axes[1].plot(x, cdf, label=f"$d_1$={d1}, $d_2$={d2}")

axes[0].set(title="PDF", xlabel="x", ylabel="f(x)", ylim=[0, 2])
axes[0].legend(fontsize=7)
axes[1].set(title="CDF", xlabel="x", ylabel="F(x)")
axes[1].legend(fontsize=7)
fig.tight_layout()
fig.show()
../../../_images/d39de5d1923277d875cb16b3db831f8614b30b2e3f6dd2215882a79261dfe247.png

性質#

  • \(X \sim F(d_1, d_2)\)のとき\(1/X \sim F(d_2, d_1)\)（自由度が入れ替わる）

  • \(T \sim t_{(n)}\)のとき\(T^2 \sim F(1, n)\)（t分布の二乗はF分布）

  • \(d_1 = 1\)のとき、\(F(1, d_2)\)はt分布の二乗と一致

  • \(d_2 \to \infty\)のとき\(d_1 \cdot F(d_1, d_2) \to \chi^2_{(d_1)}\)

  • 非負の値のみをとる右に裾の長い分布

応用例#

  • F検定: 2つの母分散の比の検定（等分散性の検定）

  • 分散分析（ANOVA）: 群間分散と群内分散の比による群間差の検定

  • 回帰分析におけるモデル全体の有意性検定

  • 回帰分析におけるネストされたモデルの比較

参考文献#

Contents