一様分布

一様分布#

概要#

一様分布（uniform distribution）は、区間\([a, b]\)上のすべての値が等しい確率密度をもつ連続確率分布である。最も単純な連続確率分布であり、\(U(a,b)\)と表記される。

乱数生成の基礎となる分布であり、逆関数法などを通じて他の確率分布に従う乱数を生成する出発点として重要な役割を果たす。

確率密度関数#

\[\begin{split} f(x \mid a, b) = \begin{cases} \dfrac{1}{b-a} & a \leq x \leq b \\ 0 & \text{otherwise} \end{cases} \end{split}\]

  • \(a\): 下限（location parameter）

  • \(b\): 上限（\(b > a\)）

累積分布関数#

\[\begin{split} F(x) = \begin{cases} 0 & x < a \\ \dfrac{x-a}{b-a} & a \leq x \leq b \\ 1 & x > b \end{cases} \end{split}\]

期待値・分散#

\[ E[X] = \frac{a+b}{2} \]
\[ V[X] = \frac{(b-a)^2}{12} \]

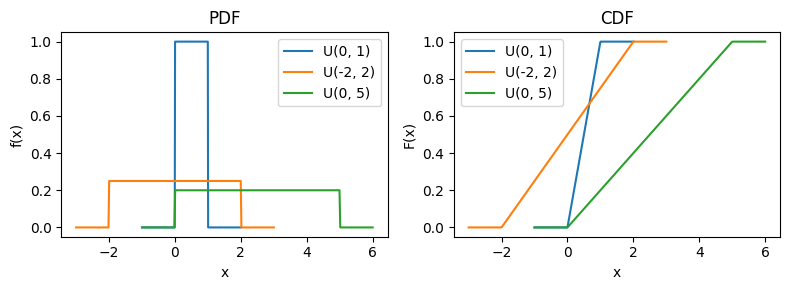
図#

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import uniform

fig, axes = plt.subplots(1, 2, figsize=[8, 3])

params = [(0, 1), (-2, 2), (0, 5)]
for a, b in params:
    x = np.linspace(a - 1, b + 1, 300)
    pdf = uniform.pdf(x, loc=a, scale=b - a)
    axes[0].plot(x, pdf, label=f"U({a}, {b})")

    cdf = uniform.cdf(x, loc=a, scale=b - a)
    axes[1].plot(x, cdf, label=f"U({a}, {b})")

axes[0].set(title="PDF", xlabel="x", ylabel="f(x)")
axes[0].legend()
axes[1].set(title="CDF", xlabel="x", ylabel="F(x)")
axes[1].legend()
fig.tight_layout()
fig.show()
../../../_images/31b21fc9e36d81c959804d75f3e0c4e8c2ba0e084f4c2e638f0fd59b6879338b.png

性質#

  • 最大エントロピー性: 区間\([a,b]\)上の連続分布のうち、エントロピーが最大となるのは一様分布である

  • 逆関数法: \(U \sim U(0,1)\)のとき、\(F^{-1}(U)\)は累積分布関数\(F\)をもつ分布に従う。これを逆関数法（inverse transform sampling）といい、乱数生成の基本的な手法である

  • 順序統計量: \(U(0,1)\)からの\(n\)個の独立な標本の\(k\)番目の順序統計量はベータ分布\(\text{Beta}(k, n-k+1)\)に従う

応用例#

  • 擬似乱数生成の基礎（他の分布からの乱数生成の出発点）

  • モンテカルロシミュレーション

  • ベイズ推定における無情報事前分布

  • 丸め誤差のモデリング

参考文献#

Contents