ガンマ分布

ガンマ分布#

概要#

ガンマ分布（gamma distribution）は非負の実数直線上の代表的な確率分布である。指数分布やカイ二乗分布を特殊ケースとして含む柔軟な分布族であり、待ち時間や生存時間のモデリング、ベイズ統計における共役事前分布として広く用いられる。

確率密度関数#

shape-scale パラメタリゼーション#

\[ f(x \mid \alpha, \beta) = \frac{1}{\Gamma(\alpha)} \frac{1}{\beta} \left( \frac{x}{\beta} \right) ^{\alpha-1} e^{-x/\beta} , \quad x > 0 \]

  • \(\alpha > 0\): shape parameter（形状パラメータ）

  • \(\beta > 0\): scale parameter（尺度パラメータ）

shape-rate パラメタリゼーション#

尺度変換\(\lambda = 1/\beta\)を行った

\[ f(x \mid \alpha, \lambda) = \frac{\lambda^\alpha}{\Gamma(\alpha)} x^{\alpha-1} e^{-\lambda x} ,\quad x > 0 \]

という定義も使われる（\(\lambda\)はrate parameterと呼ばれる）。

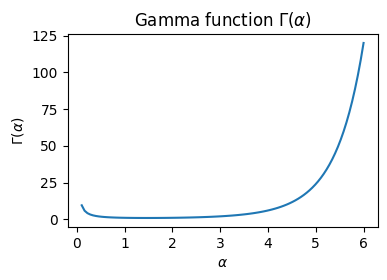
ガンマ関数#

ここで\(\Gamma(\alpha)\)はガンマ関数（gamma function）

\[ \Gamma(\alpha) = \int^{\infty}_0 y^{\alpha-1} e^{-y} dy \]

自然数\(n\)に対して\(\Gamma(n) = (n-1)!\)が成り立つ。また\(\Gamma(1/2) = \sqrt{\pi}\)である。

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gamma

x = np.linspace(0.1, 6, 100)
y = gamma(x)

fig, ax = plt.subplots(figsize=[4, 2.5])
ax.plot(x, y)
ax.set(title=r"Gamma function $\Gamma(\alpha)$", xlabel=r"$\alpha$", ylabel=r"$\Gamma(\alpha)$")
fig.show()
../../../_images/5eb49b00600d867c58408fd0e824356d09d952dcba92a432a770950ee85d88e9.png

累積分布関数#

\[ F(x) = \frac{\gamma(\alpha, x/\beta)}{\Gamma(\alpha)} \]

ここで\(\gamma(\alpha, x)\)は下側不完全ガンマ関数。一般に閉じた形では表せない。

期待値・分散#

shape-scale パラメタリゼーションの場合：

\[ E[X] = \alpha\beta \]
\[ V[X] = \alpha\beta^2 \]

shape-rate パラメタリゼーション（\(\lambda = 1/\beta\)）の場合：

\[ E[X] = \frac{\alpha}{\lambda}, \quad V[X] = \frac{\alpha}{\lambda^2} \]

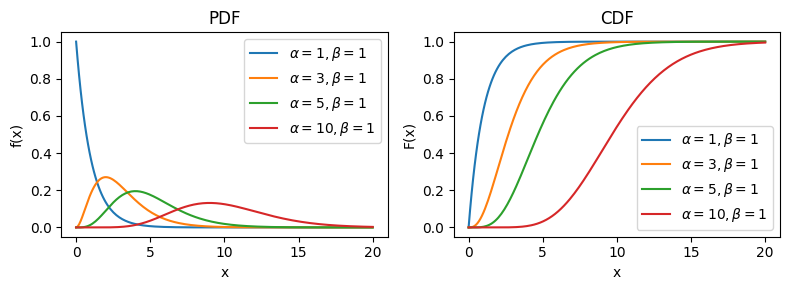
図#

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma as gamma_dist

x = np.linspace(0, 20, 200)

fig, axes = plt.subplots(1, 2, figsize=[8, 3])
for alpha in [1, 3, 5, 10]:
    pdf = gamma_dist.pdf(x, alpha)
    axes[0].plot(x, pdf, label=fr"$\alpha={alpha}, \beta=1$")
    cdf = gamma_dist.cdf(x, alpha)
    axes[1].plot(x, cdf, label=fr"$\alpha={alpha}, \beta=1$")

axes[0].set(title="PDF", xlabel="x", ylabel="f(x)")
axes[0].legend()
axes[1].set(title="CDF", xlabel="x", ylabel="F(x)")
axes[1].legend()
fig.tight_layout()
fig.show()
../../../_images/9335a754382a45a0734cb321fba773c7b88733611b24ee90619ad6885aca4eb1.png

性質#

  • \(\alpha=1\)のとき指数分布 \(\text{Exp}(1/\beta)\)に一致する

  • \(\alpha=n/2, \beta=2\)のとき自由度\(n\)のカイ二乗分布に一致する

  • 再生性: \(X_1 \sim \text{Gamma}(\alpha_1, \beta), X_2 \sim \text{Gamma}(\alpha_2, \beta)\)が独立なら\(X_1 + X_2 \sim \text{Gamma}(\alpha_1+\alpha_2, \beta)\)

  • 指数型分布族に属する

  • ポアソン分布の共役事前分布である

  • 尺度変換\(Y = X/\beta\)を行うと、\(Y\)の分布は\(\beta\)に依存しない標準形\(\frac{1}{\Gamma(\alpha)} y^{\alpha-1} e^{-y}\)となる

応用例#

  • 待ち時間のモデリング（ポアソン過程で\(\alpha\)個の事象が起きるまでの時間）

  • ベイズ統計におけるポアソン分布のrate parameterの共役事前分布

  • 保険数理における請求額の分布

  • 降雨量のモデリング

参考文献#

Contents