幾何分布#
概要#
独立なベルヌーイ試行を行い、初めて成功するまでの失敗回数（または試行回数）の分布。指数分布の離散版とみなすことができ、離散確率分布の中で唯一の無記憶性をもつ分布である。
確率質量関数#
幾何分布の定義には2つの慣習がある。
失敗回数版（主な定義）#
成功するまでの 失敗回数 \(X\) が \(k\) となる確率は
\[
P(X=k \mid p) = p(1-p)^k, \quad k=0,1,2,\dots
\]
成功するまでの失敗が \(k\) 回、成功が1回という試行になるため、成功の確率を \(p\)、失敗の確率を \(1-p\) とおくとこの式が導かれる。
試行回数版（別の定義）#
初めて成功するまでの 試行回数 \(Y\) が \(k\) となる確率は
\[
P(Y=k \mid p) = p(1-p)^{k-1}, \quad k=1,2,3,\dots
\]
\(Y = X + 1\) の関係にある。scipyの geom はこちらの試行回数版を採用している。
\(p\): 各試行での成功確率
累積分布関数#
失敗回数版の累積分布関数は、
\[
F(k) = P(X \leq k) = 1 - (1-p)^{k+1}, \quad k = 0, 1, 2, \dots
\]
導出
\[\begin{split}
\begin{align}
F(k) &= \sum_{i=0}^{k} p(1-p)^i \\
&= p \sum_{i=0}^{k} (1-p)^i \\
&= p \cdot \frac{1 - (1-p)^{k+1}}{1 - (1-p)} \\
&= p \cdot \frac{1 - (1-p)^{k+1}}{p} \\
&= 1 - (1-p)^{k+1}
\end{align}
\end{split}\]
ここで等比級数の和の公式 \(\sum_{i=0}^{n} r^i = \frac{1 - r^{n+1}}{1 - r}\) を用いた。
期待値・分散#
\[
E[X] = \frac{1-p}{p}
\]
\[
V[X] = \frac{1-p}{p^2}
\]
期待値の導出#
\(q = 1 - p\) とおく。
\[\begin{split}
\begin{align}
E[X] &= \sum_{k=0}^{\infty} k \cdot p q^k \\
&= p \sum_{k=0}^{\infty} k q^k \\
&= p \cdot q \sum_{k=1}^{\infty} k q^{k-1}
\end{align}
\end{split}\]
ここで等比級数 \(\sum_{k=0}^{\infty} q^k = \frac{1}{1-q}\) の両辺を \(q\) で微分すると
\[
\sum_{k=1}^{\infty} k q^{k-1} = \frac{1}{(1-q)^2} = \frac{1}{p^2}
\]
したがって、
\[
E[X] = p \cdot q \cdot \frac{1}{p^2} = \frac{q}{p} = \frac{1-p}{p}
\]
分散の導出#
\(V[X] = E[X^2] - (E[X])^2\) を用いる。\(E[X(X-1)]\) を求めるため、等比級数の2階微分を利用する。
\[
\sum_{k=2}^{\infty} k(k-1) q^{k-2} = \frac{2}{(1-q)^3} = \frac{2}{p^3}
\]
\[
E[X(X-1)] = p q^2 \cdot \frac{2}{p^3} = \frac{2q^2}{p^2}
\]
\[
E[X^2] = E[X(X-1)] + E[X] = \frac{2q^2}{p^2} + \frac{q}{p} = \frac{2q^2 + qp}{p^2} = \frac{q(2q + p)}{p^2} = \frac{q(q + 1)}{p^2}
\]
\[
V[X] = E[X^2] - (E[X])^2 = \frac{q(q+1)}{p^2} - \frac{q^2}{p^2} = \frac{q}{p^2} = \frac{1-p}{p^2}
\]
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import geom
fig, axes = plt.subplots(1, 2, figsize=[8, 3])
for p in [0.2, 0.5, 0.8]:
k = np.arange(0, 15)
# scipy's geom uses "number of trials" convention, shift by 1
pmf = geom.pmf(k + 1, p=p)
axes[0].bar(k + (p - 0.5) * 0.3, pmf, width=0.25, alpha=0.7, label=f"p={p}")
cdf = geom.cdf(k + 1, p=p)
axes[1].step(k, cdf, where='mid', label=f"p={p}")
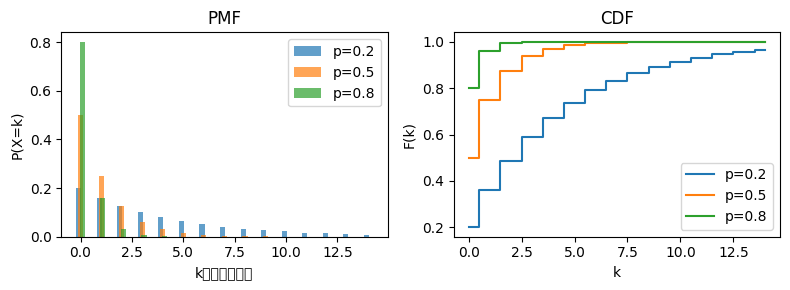
axes[0].set(title="PMF", xlabel="k\uff08\u5931\u6557\u56de\u6570\uff09", ylabel="P(X=k)")
axes[0].legend()
axes[1].set(title="CDF", xlabel="k", ylabel="F(k)")
axes[1].legend()
fig.tight_layout()
fig.show()
/tmp/ipykernel_11733/761145532.py:20: UserWarning: Glyph 65288 (\N{FULLWIDTH LEFT PARENTHESIS}) missing from current font.
fig.tight_layout()
/tmp/ipykernel_11733/761145532.py:20: UserWarning: Glyph 22833 (\N{CJK UNIFIED IDEOGRAPH-5931}) missing from current font.
fig.tight_layout()
/tmp/ipykernel_11733/761145532.py:20: UserWarning: Glyph 25943 (\N{CJK UNIFIED IDEOGRAPH-6557}) missing from current font.
fig.tight_layout()
/tmp/ipykernel_11733/761145532.py:20: UserWarning: Glyph 22238 (\N{CJK UNIFIED IDEOGRAPH-56DE}) missing from current font.
fig.tight_layout()
/tmp/ipykernel_11733/761145532.py:20: UserWarning: Glyph 25968 (\N{CJK UNIFIED IDEOGRAPH-6570}) missing from current font.
fig.tight_layout()
/tmp/ipykernel_11733/761145532.py:20: UserWarning: Glyph 65289 (\N{FULLWIDTH RIGHT PARENTHESIS}) missing from current font.
fig.tight_layout()
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/IPython/core/events.py:82: UserWarning: Glyph 65288 (\N{FULLWIDTH LEFT PARENTHESIS}) missing from current font.
func(*args, **kwargs)
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/IPython/core/events.py:82: UserWarning: Glyph 22833 (\N{CJK UNIFIED IDEOGRAPH-5931}) missing from current font.
func(*args, **kwargs)
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/IPython/core/events.py:82: UserWarning: Glyph 25943 (\N{CJK UNIFIED IDEOGRAPH-6557}) missing from current font.
func(*args, **kwargs)
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/IPython/core/events.py:82: UserWarning: Glyph 22238 (\N{CJK UNIFIED IDEOGRAPH-56DE}) missing from current font.
func(*args, **kwargs)
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/IPython/core/events.py:82: UserWarning: Glyph 25968 (\N{CJK UNIFIED IDEOGRAPH-6570}) missing from current font.
func(*args, **kwargs)
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/IPython/core/events.py:82: UserWarning: Glyph 65289 (\N{FULLWIDTH RIGHT PARENTHESIS}) missing from current font.
func(*args, **kwargs)
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/IPython/core/pylabtools.py:170: UserWarning: Glyph 65288 (\N{FULLWIDTH LEFT PARENTHESIS}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/IPython/core/pylabtools.py:170: UserWarning: Glyph 22833 (\N{CJK UNIFIED IDEOGRAPH-5931}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/IPython/core/pylabtools.py:170: UserWarning: Glyph 25943 (\N{CJK UNIFIED IDEOGRAPH-6557}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/IPython/core/pylabtools.py:170: UserWarning: Glyph 22238 (\N{CJK UNIFIED IDEOGRAPH-56DE}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/IPython/core/pylabtools.py:170: UserWarning: Glyph 25968 (\N{CJK UNIFIED IDEOGRAPH-6570}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/home/runner/work/notes/notes/.venv/lib/python3.10/site-packages/IPython/core/pylabtools.py:170: UserWarning: Glyph 65289 (\N{FULLWIDTH RIGHT PARENTHESIS}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
性質#
無記憶性: \(P(X > s + t \mid X > s) = P(X > t)\)。離散分布の中で無記憶性を持つのは幾何分布のみ。これは指数分布の無記憶性の離散版。
連続版の対応物は指数分布
\(\text{Geo}(p)\) は負の二項分布 \(\text{NB}(1, p)\) の特殊ケース
応用例#
アポ取りの電話をかけて何回目にアポが取れるか
製造ラインで初めて不良品が出るまでの良品数
サイコロで初めて6が出るまでの回数
ネットワーク通信で初めてパケットロスが起きるまでの成功送信数