ベータ分布

ベータ分布#

概要#

ベータ分布（beta distribution）は、区間\([0, 1]\)上で定義される連続確率分布である。2つの形状パラメータによって非常に多様な分布形状を表現でき、確率や割合のモデリングに適している。

ベイズ統計においてベルヌーイ分布・二項分布の共役事前分布として重要な役割を果たす。

確率密度関数#

\[ f(x \mid \alpha, \beta) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha, \beta)}, \quad 0 \leq x \leq 1 \]

  • \(\alpha > 0\): 形状パラメータ

  • \(\beta > 0\): 形状パラメータ

ここで\(B(\alpha, \beta)\)はベータ関数

\[ B(\alpha, \beta) = \int_0^1 t^{\alpha-1}(1-t)^{\beta-1} dt = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)} \]

累積分布関数#

\[ F(x) = I_x(\alpha, \beta) = \frac{B(x; \alpha, \beta)}{B(\alpha, \beta)} \]

ここで\(I_x(\alpha, \beta)\)は正則化不完全ベータ関数、\(B(x; \alpha, \beta) = \int_0^x t^{\alpha-1}(1-t)^{\beta-1}dt\)は不完全ベータ関数である。

期待値・分散#

\[ E[X] = \frac{\alpha}{\alpha+\beta} \]
\[ V[X] = \frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)} \]

最頻値（\(\alpha > 1, \beta > 1\)のとき）：

\[ \text{mode} = \frac{\alpha - 1}{\alpha + \beta - 2} \]

図#

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import beta

x = np.linspace(0.001, 0.999, 300)

fig, axes = plt.subplots(1, 2, figsize=[8, 3])

params = [(0.5, 0.5), (1, 1), (2, 2), (2, 5), (5, 2)]
for a, b in params:
    pdf = beta.pdf(x, a, b)
    axes[0].plot(x, pdf, label=fr"$\alpha={a}, \beta={b}$")
    cdf = beta.cdf(x, a, b)
    axes[1].plot(x, cdf, label=fr"$\alpha={a}, \beta={b}$")

axes[0].set(title="PDF", xlabel="x", ylabel="f(x)", ylim=[0, 4])
axes[0].legend(fontsize=7)
axes[1].set(title="CDF", xlabel="x", ylabel="F(x)")
axes[1].legend(fontsize=7)
fig.tight_layout()
fig.show()
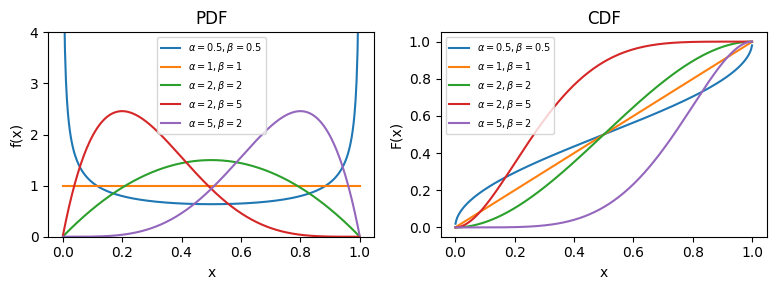
../../../_images/86c7dca6f897e71cae3ce19cd20fc654a5fdb35e4a8699fba9d3359ad8518fc0.png

性質#

  • \(\alpha=\beta=1\)のとき\([0,1]\)上の一様分布に一致する

  • \(\alpha=\beta\)のとき\(x=0.5\)に関して対称な分布になる

  • \(\alpha < 1, \beta < 1\)のとき U 字型の分布になる

  • 共役事前分布: ベルヌーイ分布・二項分布の尤度に対し、ベータ分布は共役事前分布となる。すなわち事前分布\(\text{Beta}(\alpha, \beta)\)のもとで\(k\)回の成功と\(n-k\)回の失敗を観測すると、事後分布は\(\text{Beta}(\alpha+k, \beta+n-k)\)

  • \(U(0,1)\)からの\(n\)個の標本の第\(k\)順序統計量は\(\text{Beta}(k, n-k+1)\)に従う

  • \(X \sim \text{Gamma}(\alpha, \theta), Y \sim \text{Gamma}(\beta, \theta)\)が独立なら\(\frac{X}{X+Y} \sim \text{Beta}(\alpha, \beta)\)

応用例#

  • ベイズ統計における成功確率の事前分布・事後分布

  • A/Bテストにおけるコンバージョン率のモデリング（Thompson sampling）

  • プロジェクト管理におけるPERT（タスク完了時間の不確実性モデリング）

  • 生態学における種の比率のモデリング

参考文献#

Contents