ワイブル分布

ワイブル分布#

概要#

ワイブル分布（Weibull distribution）は、生存解析・信頼性工学で基本となる分布である。ハザード関数が時間のべき乗に比例するという仮定から導かれ、指数分布を特殊ケースとして含む。

形状パラメータによって故障率の時間変化パターン（増加・一定・減少）を柔軟に表現できるため、製品の寿命分析や風速のモデリングなど幅広い応用がある。

確率密度関数#

\[ f(x \mid a, b) = a b x^{b-1} \exp\{ -a x^b \}, \quad x > 0 \]

  • \(a > 0\): scale に関するパラメータ

  • \(b > 0\): shape parameter（形状パラメータ）

ハザード関数からの導出#

時間の経過とともに死亡（故障）しやすくなるようなハザード関数として

\[ \lambda(x) = a b x^{b-1}, \quad a > 0, b > 0 \]

を考える。これの積分は

\[ \int_0^x \lambda(t) dt = \int_0^x a b t^{b-1} dt = a b\left[\frac{1}{b} t^b \right]_0^x = a x^b \]

であるので、指数分布のページで導出した

\[ f(x) = \lambda(x) \exp\left\{-\int_0^x \lambda(t) dt\right\} \]

に代入すると、ワイブル分布の密度関数が得られる。

累積分布関数#

\[ F(x) = 1 - \exp\{-a x^b\} \]

期待値・分散#

\[ E[X] = a^{-1/b} \Gamma\left(1 + \frac{1}{b}\right) \]
\[ V[X] = a^{-2/b} \left[\Gamma\left(1 + \frac{2}{b}\right) - \left(\Gamma\left(1 + \frac{1}{b}\right)\right)^2 \right] \]

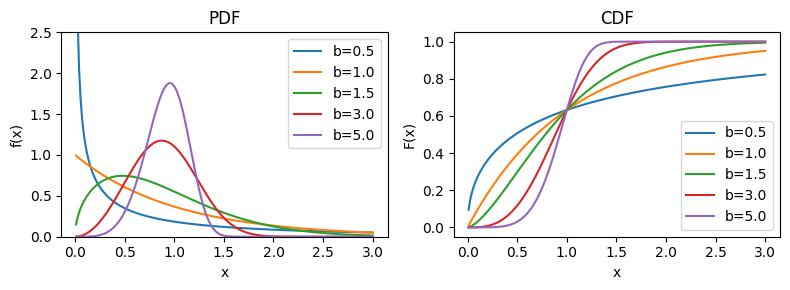
図#

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import weibull_min

x = np.linspace(0.01, 3, 200)

fig, axes = plt.subplots(1, 2, figsize=[8, 3])

for b in [0.5, 1.0, 1.5, 3.0, 5.0]:
    pdf = weibull_min.pdf(x, c=b)
    axes[0].plot(x, pdf, label=f"b={b}")
    cdf = weibull_min.cdf(x, c=b)
    axes[1].plot(x, cdf, label=f"b={b}")

axes[0].set(title="PDF", xlabel="x", ylabel="f(x)", ylim=[0, 2.5])
axes[0].legend()
axes[1].set(title="CDF", xlabel="x", ylabel="F(x)")
axes[1].legend()
fig.tight_layout()
fig.show()
../../../_images/6bed7fb24328652fb2cedcef30674e2fb14474ed4650cd68c9c91d2494bdaf0f.png

性質#

  • \(b=1\)のとき指数分布\(\text{Exp}(a)\)に一致する（ハザード関数が定数）

  • \(b > 1\)のときハザード関数は増加関数（時間とともに故障しやすくなる：摩耗故障）

  • \(b < 1\)のときハザード関数は減少関数（初期故障型）

  • \(b=2\)のときレイリー分布に一致する

  • ハザード関数\(\lambda(x) = abx^{b-1}\)がべき関数であることがワイブル分布を特徴づける

応用例#

  • 信頼性工学における製品寿命の分析

  • 生存分析における生存時間のモデリング

  • 風速の分布のモデリング（風力発電の設計に使用）

  • 材料科学における破壊強度の分布

参考文献#

Contents