ベルヌーイ分布

ベルヌーイ分布#

概要#

\(p\)の確率で「成功」、\(1-p\)の確率で「失敗」する実験を行うことを ベルヌーイ試行 という。ベルヌーイ分布は、このベルヌーイ試行の結果を表す最も基本的な離散確率分布であり、多くの離散確率分布の基礎となる。

確率質量関数#

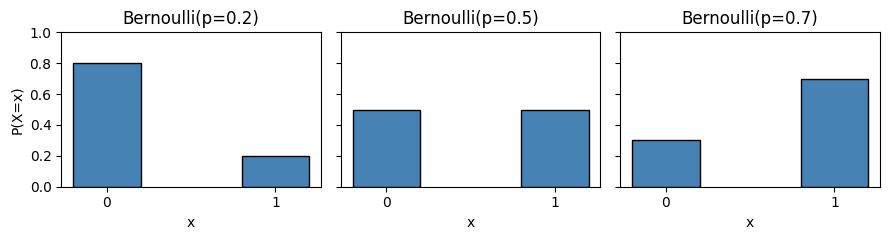
確率変数\(X\)がベルヌーイ分布 \(\text{Bernoulli}(p)\) に従うとき、確率質量関数（PMF）は次のように表される。

\[\begin{split} P(X=x|p) = \begin{cases} p & x = 1 \\ 1-p & x = 0 \end{cases} \end{split}\]

  • \(p\): 成功確率 (\(0 \leq p \leq 1\))

  • \(x=1\): 成功、\(x=0\): 失敗

通常はこれをひとつにまとめて書く

\[ P(X=x|p) = p^x (1-p)^{1-x}, \quad x \in \{0, 1\} \]

累積分布関数#

\[\begin{split} F(x) = \begin{cases} 1-p & 0 \leq x < 1 \\ 1 & x \geq 1 \end{cases} \end{split}\]

期待値・分散#

期待値#

\[ E[X] = \sum_{x \in \{0,1\}} x \cdot P(X=x) = 0 \cdot (1-p) + 1 \cdot p = p \]

分散#

\(V[X] = E[X^2] - (E[X])^2\) を用いる。\(X \in \{0, 1\}\) より \(X^2 = X\) であるから、

\[ E[X^2] = E[X] = p \]

したがって、

\[ V[X] = E[X^2] - (E[X])^2 = p - p^2 = p(1-p) \]

Hide code cell source

 
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import bernoulli

x = [0, 1]
p_values = [0.2, 0.5, 0.7]

fig, axes = plt.subplots(1, len(p_values), figsize=[9, 2.5], sharey=True)

for ax, p in zip(axes, p_values):
    pmf = bernoulli.pmf(x, p)
    ax.bar(x, pmf, width=0.4, color="steelblue", edgecolor="black")
    ax.set(title=f"Bernoulli(p={p})", xlabel="x", xticks=[0, 1], ylim=[0, 1])

axes[0].set_ylabel("P(X=x)")
fig.tight_layout()
../../../_images/ca168a86d753d0289009af1dda1afa3ceb6a4d95b285a268ca249e14ba4003f9.png

性質#

  • 二項分布 \(B(1, p)\) の特殊ケース

  • 指数型分布族に属する

  • 十分統計量は \(\sum X_i\)

応用例#

  • コインの表裏

  • 顧客の成約可否

  • A/Bテストでのコンバージョン

  • 品質管理での良品・不良品判定

Contents