一般化部分採点モデル#
概要#
一般化部分得点モデル（Generalized Partial Credit Model: GPCM, Muraki, 1992） は多値の順序尺度の反応を扱えるIRTモデル。
一般化部分得点モデル（Generalized Partial Credit Model: GPCM）
被験者 \(i\)、項目 \(j\)、カテゴリ \(k = 1,\dots,K\) に対して
\[
P(y_{ij}=k)
=
\frac{
\exp\!\left(\sum_{c=1}^{k} a_j(\theta_i - b_{jc})\right)
}{
\sum_{l=0}^{K}
\exp\!\left(\sum_{c=1}^{l} a_j(\theta_i - b_{jc})\right)
}
\]
\(a_j\)：項目 \(j\) の識別力
\(b_{jk}\)：段階 \(k-1 \to k\) の困難度
GRMとGPCMの使い分けについて#
Cook (1996) “A comparison of three polytomous item response theory models in the context of testlet scoring”
SATの実世界データとシミュレーションデータを使ってGPCMとGRMを比較した。
\(\theta\)の推定値は相関係数 0.9748 ~ 0.9921と高い相関を示した。
Dai et al. (2021) “Performance of Polytomous IRT Models With Rating Scale Data”
データ：Rの
irtplayパッケージのsimdat()関数で、GRMとGPCMの下でのデータを生成。異なるサンプルサイズ・項目数・欠損率で比較。GRM生成データをGPCMで分析すると収束しないケースが多い→やはり両モデルは若干異なる
項目母数の安定性：GPCM ＞ GRM
能力母数の精度：GRM ＞ GPCM（ただし高欠測率の時はGPCMが安定）
テスト情報量はGRMが高くなる傾向がある
考え方#
隣のカテゴリとの2択で考える#
2カテゴリの場合#
\(y_{ij}\in\{0,1\}\)とする。2PLモデルにおいては、
\[
P(y_{ij} = 1) = \frac{1}{1+ \exp[- a_j ( \theta_i - b_j)]}
, \quad
\log\left( \frac{P(y_{ij} = 1)}{1 - P(y_{ij} = 1)} \right) = a_j ( \theta_i - b_j)
\]
「\(y_{ij}=0\)の確率（カテゴリ0を選ぶ確率）」と「\(y_{ij}=1\)の確率（カテゴリ1を選ぶ確率）」の合計は1になる。そして「カテゴリ1を選ぶ確率」は
\[
P(y_{ij}=1) = \frac{P(y_{ij}=1)}{P(y_{ij}=0) + P(y_{ij}=1)}
\]
と表すことができる。
\(K\)カテゴリの場合#
これを\(K\)カテゴリ（\(k=1,2,\cdots,K\)）に一般化し、「隣り合う2つのカテゴリ\(k-1\)と\(k\)の二択において\(k\)を選ぶ確率」\(P(y_{i j}^*=k)_{k-1, k}\)とする。
\[
P(y_{i j}^*=k)_{k-1, k} := \frac{P(y_{i j}=k)}{P(y_{i j}=k)+P(y_{i j}=k-1)}
\tag{1}
\]
これは反応 \(y_{ij}\) が \(k-1\) か \(k\) のどちらかだと仮定して正規化したとき、\(k\) が選ばれる「相対的な割合」。
式\((1)\)を
\(P(y_{ij}=k)=\)の形に変形すると
\[
P(y_{ij}=k)=P(y_{ij}=k-1) \frac{P(y_{ij}^*=k)_{k-1, k}}{1-P(y_{ij}^*=k)_{k-1, k}}
\tag{2}
\]
となる。
式変形メモ
わかりやすくするため、記号を単純化する。
\[
P\left(y_{ij}^*=k\right)_{k-1, k} = P^* =\frac{P_k}{P_k+P_{k-1}}
\]
まず
\[
P^*=\frac{P_k}{P_k+P_{k-1}}
\]
の両辺に \(P_k+P_{k-1}\) を掛ける：
\[
P^*\left(P_k+P_{k-1}\right)=P_k
\]
左辺を展開：
\[
P^* P_k+P^* P_{k-1}=P_k
\]
\(P_k\) を左にまとめる：
\[\begin{split}
\begin{aligned}
& P_k-P^* P_k=P^* P_{k-1} \\
& \left(1-P^*\right) P_k=P^* P_{k-1}
\end{aligned}
\end{split}\]
両辺を \(1-P^*\) で割る：
\[
P_k=P_{k-1} \frac{P^*}{1-P^*}
\]
漸化式の形に変形#
ここで、\(k\)と\(k-1\)のカテゴリの2択であるということで、2PLMと同様にロジスティックモデルで表現できるとすると、
\[
\log \frac{P(y_{i j}^*=k)_{k-1, k}}{1-P(y_{i j}^*=k)_{k-1, k}}=a_j(\theta_i-b_{j k})
\]
と対数オッズを線形モデルで表現する形に表すことができる。この両辺に指数をとると
\[
\frac{P(y_{i j}^*=k)_{k-1, k}}{1-P(y_{i j}^*=k)_{k-1, k}} = \exp[ a_j(\theta_i-b_{j k}) ]
\]
になる。簡単のため\(\pi_{ijk} = a_j(\theta_i-b_{j k})\)とすると、式\((2)\)は
\[
\boxed{
P(y_{ij}=k)
% = P(y_{ij}=k-1) \frac{P(y_{ij}^*=k)_{k-1, k}}{1-P(y_{ij}^*=k)_{k-1, k}}
= P(y_{ij}=k-1) \exp(\pi_{ijk})
}
\]
という漸化式の形になる。言葉で書くと、「特定のカテゴリ\(k\)を選ぶ確率 \(P(y_{ij}=k)\) 」は、「 \(k-1\) を選ぶ確率 \(P(y_{ij}=k-1)\) 」と「隣のカテゴリに移るオッズ\(\exp(\pi_{ijk}) = \frac{P(y_{i j}^*=k)_{k-1, k}}{1-P(y_{i j}^*=k)_{k-1, k}}\) 」で表すことができるというもの。
例えば3カテゴリの場合は
\[\begin{split}
\begin{aligned}
P(y_{ij}=1) &= P(y_{ij}=1)\\
P(y_{ij}=2) &= P(y_{ij}=1) \exp(\pi_{ij2})\\
P(y_{ij}=3) &= \underbrace{ P(y_{ij}=1) \exp(\pi_{ij2}) }_{P(y_{ij}=2)} \exp(\pi_{ij3})\\
\end{aligned}
\end{split}\]
のようになる。つまり、\(P(y_{ij}=1)\)に\(\exp(\pi_{ijk})\)の積を掛け合わせた形ですべてのカテゴリの反応確率が表される。
\[\begin{split}
\begin{aligned}
P(y_{ij}=k)
&= P(y_{ij}=k-1)\exp(\pi_{ijk})\\
&= P(y_{ij}=k-2)\exp(\pi_{ij,k-1})\exp(\pi_{ijk})\\
&\quad \vdots\\
&= P(y_{ij}=1)\prod_{c=2}^{k}\exp(\pi_{ijc})\\
&= P(y_{ij}=1)\exp\left(\sum_{c=2}^{k}\pi_{ijc}\right)
\end{aligned}
\end{split}\]
いったん\(\pi_{ij1} = 0\)として、\(P(y_{ij}=1) = \exp(\pi_{ij1}) = 1\) を代入すると
\[
P(y_{ij}=k) = \exp\left(\sum_{c=1}^{k}\pi_{ijc}\right)
\]
正規化#
\(P(y_{ij}=1)=1\)としたため、全カテゴリの選択確率の総和が1になるとは限らない。そこで全カテゴリの総和で割って正規化する。
\[\begin{split}
\begin{aligned}
\frac{ P(y_{ij}=k) }{ \sum_{l=1}^K P(y_{ij}=l)}
&= \frac{ P(y_{ij}=k) }{ P(y_{ij}=1) + P(y_{ij}=2) + \cdots + P(y_{ij}=K) }\\
&= \frac{ \exp(\sum^k_{c=1} \pi_{ijc}) }{ \sum_{l=1}^K \exp(\sum^l_{c=1} \pi_{ijc}) }
\end{aligned}
\end{split}\]
項目特性曲線#
項目特性曲線（ICC）あるいは CRC（Category Response Curves） は 能力 \(\theta\) に対して各カテゴリ \(k\) が選ばれる確率 \(P(Y=k\mid\theta)\) を描いた曲線群
\[
P(Y=k \mid \theta)=\frac{\exp \left(\sum_{s=1}^{k-1} a\left(\theta-b_s\right)\right)}{\sum_{t=1}^K \exp \left(\sum_{s=1}^{t-1} a\left(\theta-b_s\right)\right)}, \quad k=1, \ldots, K
\]
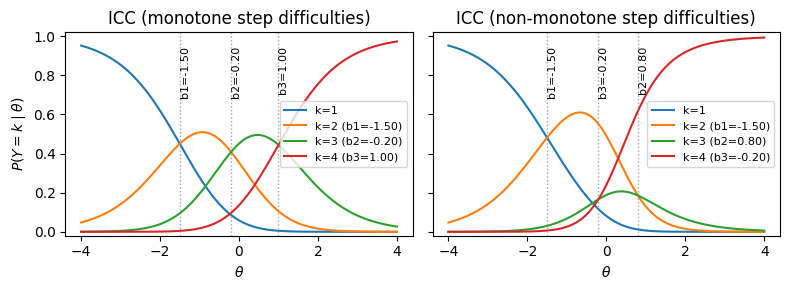
また、全体の傾向を見たい場合は能力 \(\theta\) におけるその項目の期待得点（得点で重みづけたCRC）である ESC（Expected Score Curve）
\[
\mathbb{E}[Y \mid \theta]=\sum_{k=1}^K k P(Y=k \mid \theta)
\]
というものがある。
# ESC（単調ケース）
E_mono = np.sum((np.arange(1, K+1)[None, :]) * P_mono, axis=1)
# ESC（非単調ケース）
E_nonmono = np.sum((np.arange(1, K+1)[None, :]) * P_nonmono, axis=1)
plt.figure(figsize=(5, 3))
plt.plot(theta, E_mono, label="monotone b")
plt.plot(theta, E_nonmono, linestyle="--", label="non-monotone b")
plt.xlabel(r"$\theta$")
plt.ylabel(r"$\mathbb{E}[Y\mid\theta]$")
plt.title("Expected Score Curve (ESC)")
plt.legend()
plt.tight_layout()
plt.show()
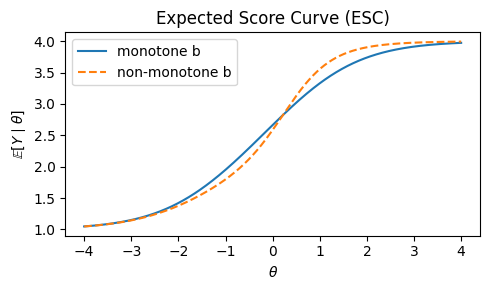
部分得点モデル#
部分得点モデル（Partial Credit Model: PCM, Masters, 1982） は Raschモデルを順序多値に拡張した IRT モデル。
\[
P(y_{ij}=k)
=
\frac{
\exp\!\left(\sum_{c=1}^{k}(\theta_i - b_{jc})\right)
}{
\sum_{l=0}^{K}
\exp\!\left(\sum_{c=1}^{l}(\theta_i - b_{jc})\right)
}
\]
あるいはロジットで表すと
\[
\log \frac{P(y_{ij}=k)}{P(y_{ij}=k-1)}
= \theta_i - b_{jk}
\]
PCMでは識別力パラメータは 存在しない（全部共通で\(a=1\)）ため扱いにくく、一般化したGPCMが提案された
一般化部分得点モデル#
一般化部分得点モデル（Generalized Partial Credit Model: GPCM, Muraki, 1992） はPCMを一般化し、項目ごとに異なる識別力\(a_j\)を導入したモデル。
\[
P(y_{ij}=k)
=
\frac{
\exp\!\left(\sum_{c=1}^{k} a_j(\theta_i - b_{jc})\right)
}{
\sum_{l=0}^{K}
\exp\!\left(\sum_{c=1}^{l} a_j(\theta_i - b_{jc})\right)
}
\]
あるいは
\[
\log \frac{P(y_{ij}=k)}{P(y_{ij}=k-1)}
= a_j(\theta_i - b_{jk})
\]
\(a_j > 0\)：項目 \(j\) の識別力
\(b_{jk}\)：段階 \(k-1 \to k\) の難易度
実装#
最尤推定ならRのmirtパッケージでgpcmを選ぶだけだが、ベイズモデリングはややこしい
BUGS#
1 model {
2 for (i in 1:n) {
3 for (j in 1:p) {
4 Y[i, j] ~ dcat(prob[i, j, 1:K[j]])
5 }
6 theta[i] ~ dnorm(mu0, tau0)
7 }
8 for (i in 1:n) {
9 for (j in 1:p) {
10 for (k in 1:K[j] ) {
11 eta[i, j, k] <- alpha[j] * (theta[i] - beta[j, k])
12 psum[i, j, k] <- sum(eta[i, j, 1:k])
13 exp.psum[i, j, k] <- exp(psum[i, j, k])
14 prob[i, j, k] <- exp.psum[i, j, k] / sum(exp.psum[i, j, 1:K[j]])
15 } } }
16 for (j in 1:p) {
17 alpha[j] ~ dlnorm(m.alpha, pr.alpha)
18 beta[j, 1] <- 0.0
19 for (k in 2:K[j]) {
20 beta[j, k] ~ dnorm(m.beta, pr.beta)
21 }
22 }
23 pr.alpha <- pow(s.alpha, −2)
24 pr.beta <- pow(s.beta, −2)
25 mu0 ~ dnorm(0, 0.01)
26 tau0 ~ dgamma(0.5, 0.5)
27 var0 <- 1/tau0
28 }
PyMC#
# データを生成
import numpy as np
import pandas as pd
def simulate_gpcm(N=1000, J=10, K=4, seed=42):
rng = np.random.default_rng(seed)
theta = rng.normal(0, 1, size=N)
a = rng.lognormal(0, 0.3, size=J)
b = rng.normal(0, 1, size=(J, K - 1)) # step difficulties（順序制約なし）
U = np.zeros((N, J), dtype=int)
for j in range(J):
inc = a[j] * (theta[:, None] - b[j][None, :]) # (N, K-1)
csum = np.cumsum(inc, axis=1) # (N, K-1)
log_num = np.concatenate([np.zeros((N, 1)), csum], axis=1) # (N, K)
mx = log_num.max(axis=1, keepdims=True)
exp_shift = np.exp(log_num - mx)
P = exp_shift / exp_shift.sum(axis=1, keepdims=True)
for i in range(N):
U[i, j] = rng.choice(K, p=P[i])
return U, theta, a, b
num_users = 1000
num_items = 20
U, true_theta, true_a, true_b = simulate_gpcm(N=num_users, J=num_items)
df = pd.DataFrame(
U,
index=[f"user_{i+1}" for i in range(num_users)],
columns=[f"question_{j+1}" for j in range(num_items)],
)
# 縦持ちへ変換
user_categories = [f"user_{i+1}" for i in range(num_users)]
item_categories = [f"question_{j+1}" for j in range(num_items)]
df_long = pd.melt(
df.reset_index(), id_vars="index", var_name="item", value_name="response",
).rename(columns={"index": "user"})
df_long["user"] = pd.Categorical(df_long["user"], categories=user_categories, ordered=True)
df_long["item"] = pd.Categorical(df_long["item"], categories=item_categories, ordered=True)
df_long.head()
| user | item | response | |
|---|---|---|---|
| 0 | user_1 | question_1 | 0 |
| 1 | user_2 | question_1 | 0 |
| 2 | user_3 | question_1 | 3 |
| 3 | user_4 | question_1 | 2 |
| 4 | user_5 | question_1 | 0 |
import pymc as pm
import pytensor.tensor as pt
user_idx = df_long["user"].cat.codes.to_numpy()
users = df_long["user"].cat.categories.to_numpy()
item_idx = df_long["item"].cat.codes.to_numpy()
items = df_long["item"].cat.categories.to_numpy()
responses = df_long["response"].to_numpy().astype("int64")
K = int(responses.max() + 1)
n_steps = K - 1
coords = {
"user": users,
"item": items,
"step": np.arange(n_steps),
"obs_id": np.arange(len(df_long)),
}
with pm.Model(coords=coords) as model:
user_idx_ = pm.Data("user_idx", user_idx, dims="obs_id")
item_idx_ = pm.Data("item_idx", item_idx, dims="obs_id")
responses_ = pm.Data("responses", responses, dims="obs_id")
theta = pm.Normal("theta", 0, 1, dims="user")
a = pm.LogNormal("a", 0, 0.5, dims="item")
b = pm.Normal("b", 0, 2, dims=("item", "step"))
# GPCM: logit_k = sum_{c=0}^{k-1} a_j (theta_i - b_{jc}), logit_0 = 0
inc = a[item_idx_][:, None] * (theta[user_idx_][:, None] - b[item_idx_])
csum = pt.cumsum(inc, axis=1)
logits = pt.concatenate([pt.zeros_like(csum[:, :1]), csum], axis=1)
p = pt.special.softmax(logits, axis=-1)
pm.Categorical("obs", p=p, observed=responses_, dims="obs_id")
%%time
with model:
idata = pm.sample(random_seed=0, draws=1000)
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, a, b]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
File <timed exec>:2
File ~/work/notes/notes/.venv/lib/python3.10/site-packages/pymc/sampling/mcmc.py:957, in sample(draws, tune, chains, cores, random_seed, progressbar, progressbar_theme, step, var_names, nuts_sampler, initvals, init, jitter_max_retries, n_init, trace, discard_tuned_samples, compute_convergence_checks, keep_warning_stat, return_inferencedata, idata_kwargs, nuts_sampler_kwargs, callback, mp_ctx, blas_cores, model, compile_kwargs, **kwargs)
953 t_sampling = time.time() - t_start
955 # Packaging, validating and returning the result was extracted
956 # into a function to make it easier to test and refactor.
--> 957 return _sample_return(
958 run=run,
959 traces=trace if isinstance(trace, ZarrTrace) else traces,
960 tune=tune,
961 t_sampling=t_sampling,
962 discard_tuned_samples=discard_tuned_samples,
963 compute_convergence_checks=compute_convergence_checks,
964 return_inferencedata=return_inferencedata,
965 keep_warning_stat=keep_warning_stat,
966 idata_kwargs=idata_kwargs or {},
967 model=model,
968 )
File ~/work/notes/notes/.venv/lib/python3.10/site-packages/pymc/sampling/mcmc.py:1042, in _sample_return(run, traces, tune, t_sampling, discard_tuned_samples, compute_convergence_checks, return_inferencedata, keep_warning_stat, idata_kwargs, model)
1040 # Pick and slice chains to keep the maximum number of samples
1041 if discard_tuned_samples:
-> 1042 traces, length = _choose_chains(traces, tune)
1043 else:
1044 traces, length = _choose_chains(traces, 0)
File ~/work/notes/notes/.venv/lib/python3.10/site-packages/pymc/backends/base.py:624, in _choose_chains(traces, tune)
622 lengths = [max(0, len(trace) - tune) for trace in traces]
623 if not sum(lengths):
--> 624 raise ValueError("Not enough samples to build a trace.")
626 idxs = np.argsort(lengths)
627 l_sort = np.array(lengths)[idxs]
ValueError: Not enough samples to build a trace.
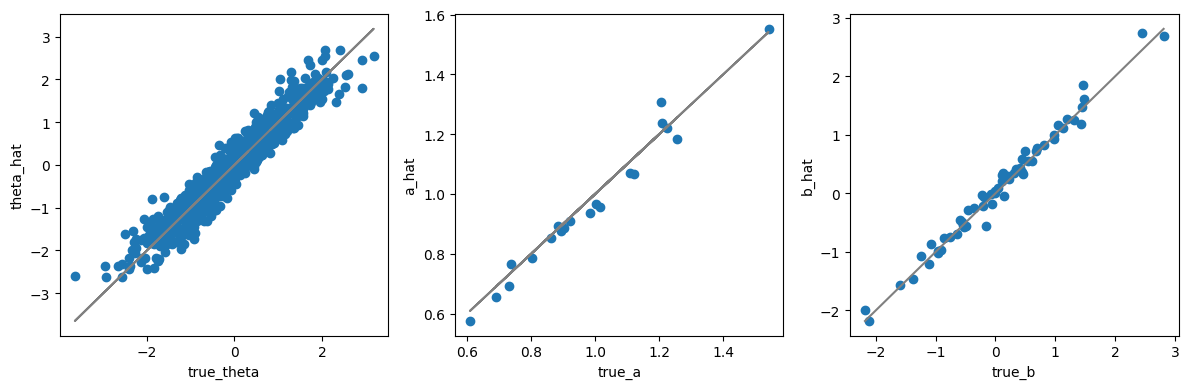
import matplotlib.pyplot as plt
post_mean = idata.posterior.mean(dim=["chain", "draw"])
fig, axes = plt.subplots(figsize=[12, 4], ncols=3)
ax = axes[0]
ax.scatter(true_theta, post_mean["theta"])
ax.plot(true_theta, true_theta, color="gray")
_ = ax.set(xlabel="true_theta", ylabel="theta_hat")
ax = axes[1]
ax.scatter(true_a, post_mean["a"])
ax.plot(true_a, true_a, color="gray")
_ = ax.set(xlabel="true_a", ylabel="a_hat")
ax = axes[2]
b_true = true_b.flatten()
b_hat = post_mean["b"].to_numpy().flatten()
ax.scatter(b_true, b_hat)
lims = [b_true.min(), b_true.max()]
ax.plot(lims, lims, color="gray")
_ = ax.set(xlabel="true_b", ylabel="b_hat")
plt.tight_layout()
